Тема 4. Асимметричные криптосистемы

Цели и задачи изучения темы

Целью данной темы является рассмотрение вопросов построения асимметричных криптосистем, хэш-функций и электронных цифровых подписей.

Алгоритмы шифрования с открытым ключом

Одной из основных проблем при практическом использовании рассмотренных симметричных систем шифрования является проблема распределения секретных ключей между абонентами и проблема хранения этих ключей.

Для решения этих проблемы на основе результатов, полученных классической и современной алгеброй, были предложены асимметричныекриптосистемы. Суть их состоит в том, что каждым адресатом информационного обмена генерируются два ключа, связанные между собой по определенному правилу. Один ключ объявляется открытым, а другой закрытым. Открытый ключ публикуется и доступен любому, кто желает послать сообщение адресату. Секретный ключ сохраняется в тайне.

Все асимметричные криптографические системы основаны на использовании односторонних функций с секретом.

Рассмотрим в общем виде принцип использования односторонних функций с секретом для шифрования сообщений. Каждый абонент криптосистемы выбирает некоторую одностороннюю функцию 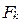с секретом k. Функции 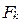всех абонентов заносятся в общедоступный справочник, но значение секрета k каждый абонент, как и следует из названия, держит в секрете. Если абонент B хочет переслать сообщение M абоненту A, он извлекает из справочника функцию 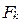абонента A и с ее помощью вычисляет C = F_k(M). Шифртекст C пересылается абоненту A, который по нему вычисляет исходное сообщение M, обратив функцию 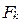с помощью секрета k. Расшифровать сообщение может только абонент A, поскольку кроме него никто не знает секрет k.

Обычно функции шифрования 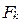для разных абонентов вычисляются по одному и тому же заранее установленному алгоритму, но в зависимости от некоторого параметра. У каждого абонента такой параметр свой. Этот параметр называется открытымключом данного абонента, поэтому асимметричные криптосистемы называют также криптосистемами с открытым ключом.

Наиболее известными криптосистемами с открытым ключом являются RSA, Диффи-Хеллмана, Эль Гамаля и криптосистема на основе эллиптических кривых.

Криптосистема RSA

Алгоритм RSA предложили в 1978 г. три автора: Р.Райвест (Rivest), А.Шамир (Shamir) и А.Адлеман (Adleman). Алгоритм получил свое название по первым буквам фамилий его авторов. Алгоритм RSA стал первым полноценным алгоритмом с открытым ключом, который может работать как в режиме шифрования данных, так и в режиме электронной цифровой подписи.

Надежность алгоритма основывается на трудности факторизации больших чисел.

В криптосистеме RSA открытый ключ e, секретный ключ d открытый текст М и шифртекст С принадлежат множеству целых чисел

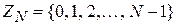
где N – модуль: 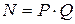. Здесь Р и Q – случайные большие простые числа. Для обеспечения максимальной безопасности выбирают Р и Q равной длины и хранят в секрете.

Множество Z_N с операциями сложения и умножения по модулю N образует арифметику по модулю N.

Число e выбирают случайным образом так, чтобы выполнялись условия:

,

,

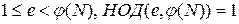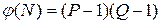где 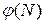– функция Эйлера, НОД(a,b) – наибольший общий делитель чисел a и b. Функция Эйлера 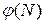указывает количество положительных целых чисел в интервале от 1 до N, которые взаимно просты с N. Второе из указанных выше условий означает, что e и функция Эйлера 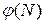должны быть взаимно простыми. Это гарантирует существование величины d, такой, что

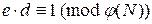или .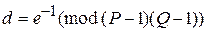

В RSA число e рассматривают как открытый ключ и используют для шифрования данных, а d – как секретный ключ для расшифрования.

Вычислить секретный ключ d по известным значениям e и 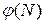можно с помощью расширенного алгоритма Евклида, который позволяет решить следующую задачу: даны целые неотрицательные числа a и b ( 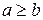), найти целые x, y, c, такие, что ax + by = c, где c = НОД(a,b).

Приведем его описание.

НА ВХОДЕ: два неотрицательных числа a и b: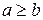

НА ВЫХОДЕ: c = НОД(a, b) и целые x, y: ax + by = c.

1. Положить x₂:=1, x₁:=0, y₂:=0, y₁:=1

2. Пока b > 0 выполнят шаги 2.1 и 2.2

2.1. q:=a div b, r:=a – qb, x:=x₂ – qx₁, y:=y₂ – qy₁

2.2. a:=b, b:=r, x₂:=x₁, x₁:=x, y₂:=y₁, y₁:=y

3. Положить c:=a, x:=x₂, y:=y₂ и возвратить (c, x, y). Конец.

Нахождение d сводится к выполнению указанного алгоритма при значениях входных параметров a = 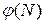и b = e. В этом случае искомое значение d есть выходной параметр y.

В RSA преобразование шифрования определяет шифртекст С через пару (открытый ключ e, открытый текст М) в соответствии со следующей формулой:

.

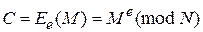В качестве алгоритма быстрого вычисления значения С используют ряд последовательных возведений в квадрат целого М и умножений на М с приведением по модулю N.

Обращение функции 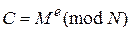, т.е. определение значения М по известным значениям С, e и N, практически не осуществимо при .

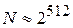Однако обратную задачу можно решить, используя пару (секретный ключ d, шифртекст С) по следующей формуле:

.

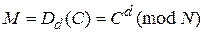Рассмотрим конкретный пример:

1) Выбрать два простых числа: P = 7, Q = 17;

2) Вычислить ;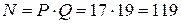

3) Вычислить ;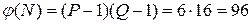

4) Выбрать е так, чтобы е было взаимнопростым с 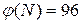и меньше, чем 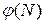: пусть е = 5;

5) Определить d так, чтобы 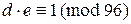и d < 96: d = 77, т.к.
77×5 = 385 = 4×96 + 1;

6) Зашифровать сообщение М = 19:
;

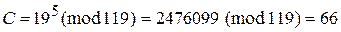7) Расшифровать C = 66: .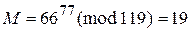

Общая процедура шифрования/расшифрования в криптосистеме RSA представляет собой следующую последовательность действий.

1. Получатель сообщения формирует значения 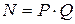, e и d, так, как было описано выше. Параметры N и e являются общедоступными, и могут быть распространенны по незащищенному каналу связи. Параметры P, Q и d являются секретными.

2. Отправитель сообщения, зная N и e, осуществляет шифрование сообщения. Если открытый текст представляет собой число 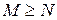, то он разбивается на блоки, каждый из которых может быть представлен в виде числа 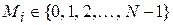. Каждый такой блок подвергается преобразованию:

.

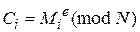В итоге получается шифртекст 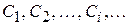, который отправляется получателю.

3. Получатель расшифровывает принятый шифртекст 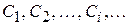, используя секретный ключ d по формуле:

.

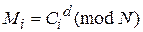В результате получается последовательность чисел 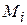, которые представляют собой открытый текст M.