Формирование математической модели. Расчётные зависимости
Исходные данные
x = _ _ , _ – аргумент функции;
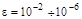– степень точности.
Расчётные зависимости
Вычислительная математика предписывает расчет функции ех в форме степенного ряда:
,
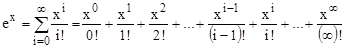где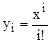 
– текущий элемент ряда,
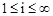– диапазон изменения параметра цикла;
i = i + 1 – закон изменения параметра цикла.
Выбор метода решения
Анализ возможности вычисления ряда (сходится – не сходится) определяет, что при малых значениях x (например, x = 0,1) ряд заведомо сходится.
Расчёт текущего значения элемента возможен:
· напрямую, т.е. по формуле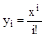 
;
· рекуррентно, т.е по формуле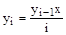 
.
Выбираем как более удобный второй метод (не требует вычисления факториала на каждом шаге). При этом параметрами цикла становятся величины yi и i, имеющие одинаковые начальные значения (теоретически yi = 0, i = 0), но разные законы изменения (yi = yi-1 x/i, i = i+1). Задаемся точностью вычисления (вначале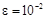 
), тогда процесс счёта (сборки ряда) должен осуществляться, пока выполняется условие 
.
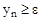Следовательно, в качестве метода решения требуется смешанный процесс – циклический вычислительный процесс с неизвестным числом повторений (итерационный) с дополнительным вычислением суммы текущих элементов до получения результата с заданной степенью точности.
Составление алгоритма решения
Анализ математической формулировки задачи позволяет сделать вывод, что первый элемент ряда (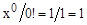 
) всегда равен единице. Поэтому в алгоритме решения (рис. 8.7), выполненном в один шаг, начальное значение искомой суммы (ex) также равно единице, а не нулю. Предусмотрено задание начального значения элемента ряда (yi-1 = 1) и его индекса (i = 1). Закон изменения индекса i = i + 1. Следовательно, алгоритм итерационного процесса содержит стандартные элементы – вход в цикл (блок 5), тело цикла (блоки 6, 7, 8, 9) и проверку условия повторения цикла или выхода из него (блок 10). Конкретное назначение основных блоков пояснено комментариями. Для улучшения наглядности организации вычислений элементы дружественности не показаны.
Программирование задачи
Идентификация переменных представлена в табл. 8.3.
Таблица 8.3
| Обозначение в алгоритме | x | 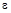 | i | ex | yi | yi-1 |
| Обозначение в программе | x | eps | i | ex | yi | yi1 |
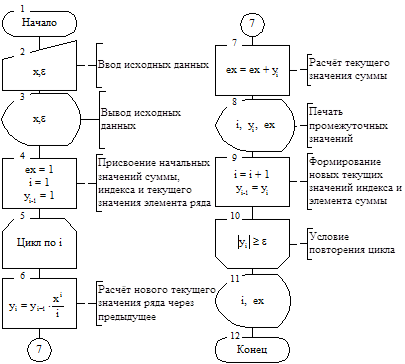
Рис. 8.7. Схема алгоритма решения задачи 8.3
С учетом таблицы идентификации на основании схемы алгоритма составим программы решения задачи.
Классический вариант программирования задачи
#include <stdlib.h> /* директивы */
#include <stdio.h> /* препроцессора */
#include <conio.h>
#include <math.h>
#include <windows.h>
main( ) /* заголовок головной функции */
{
float x, eps, yi, yi1, ex; /* описатели */
int i; /* переменных */
char buf[50]; /*описание символьного массива*/
clrscr( );
CharToOem(" Введите аргумент x: ",buf);
printf("\n %s ",buf);
scanf("%f", &x);
CharToOem(" Введите степень точности: ",buf);
printf("\n %s ",buf);
scanf("%f", &eps);
printf("\n x=%.2f eps=%.2e ", x, eps);
i = 1;
yi1 = 1;
ex = 1;
printf("\n ------------------------------------"
"\n | i | yi | ex |"
"\n -------------------------------------");
do
{
yi = yi1 * x/i;
ex = ex + yi;
printf("\n | %2d | %12.6f|%15.6f|", i, yi, ex);
i = i + 1;
yi1 = yi;
}
while( fabs( yi ) >= eps );
printf("\n ------------------------------------");
CharToOem(" Количество итераций i= ",buf);
printf("\n %s %4d \n",buf,i-1);
CharToOem(" Значение функции exp(x) = ",buf);
printf("\n %s % 15.6f\n",buf,ex);
getch( );
}
12.5 – первый блок
1e-2 исходных данных
12.5 – второй блок
1e-4 исходных данных
12.5 – третий блок
1e-6 исходных данных
Три блока численных значений позволяют проверить работоспособность программы при различных значениях степени точности.
Результаты счета представлены в приложении 8.5 (а, б, в).
Программирование задачи с графическим интерфейсом
Программирование задачи при использовании графического интерфейса предварим его разработкой. Для ввода аргумента экспоненты и степени точности расчета планируем поля редактирования (EditX, EditEps). Для вывода расчетных значений текущих элементов ряда и текущего значения функции планируем поля-списки (ListBoxYi, ListBoxExp). Вывод количества итераций и окончательного значения функции – в статические (для примера) поля (PoleIter, PoleExp).
|
|
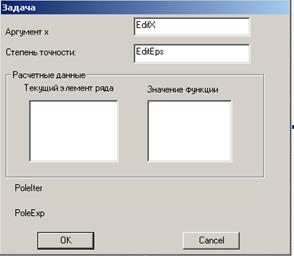
Управление процессом решения реализуем двумя командными кнопками, расположенными в нижней части окна. Назначение каждой определяется ее названием.
С учетом планируемого интерфейса выполним программирование задачи.
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
….
void TSumprDlgClient::BNClickedOk()
{
// INSERT>> Your code here.
float x, eps, yi, yi1, ex; /* описатели */
int i; /* переменных */
char buf[50]; /*описание символьного массива*/
ListBoxYi->ClearList(); /*начальная очистка*/
ListBoxExp->ClearList();/* полей вывода*/
EditX->GetText(buf,10); /*ввод */
x=atof(buf); /*аргумента х */
EditEps->GetText(buf,10); /*ввод */
eps=atof(buf); /* степени точности */
i = 1; /* присваивание */
yi1 = 1; /* начальных */
ex = 1; /* значений */
do
{
yi = yi1 * x/i; /*расчет текущего элемента ряда*/
ex = ex + yi; /*расчет текущего значения функции*/
sprintf(buf,"%8.2f",yi); /* вывод текущих*/
ListBoxYi->AddString(buf); /* значений yi*/
sprintf(buf,"%15.1f",ex); /* вывод текущих*/
ListBoxExp->AddString(buf); /* значений ex*/
i = i + 1; /*наращивание номера итерации*/
yi1 = yi; /*переприсваивание значений элементов ряда*/
}
while( fabs( yi ) >= eps );
sprintf(buf,"%s %3d","Количество итераций",i); /* вывод*/
PoleIter->SetText(buf); /* количества итераций*/
sprintf(buf,"%s %12.2f","Значение функции",ex); /* вывод*/
PoleExp->SetText(buf); /* значения функции*/
}
12.5 – первый блок
1e-2 данных
12.5 – второй блок
1e-4 данных
12.5 – третий блок
1e-6 данных
Три блока численных значений позволяют проверить работоспособность программы при различных значениях степени точности.
Результаты счета представлены в приложении 8.6.