Методика множественного регрессионного анализа

В множественном регрессионном анализе исследуется связь между несколькими независимыми переменными (предикторами) 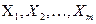и результативным признаком (откликом) 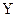. Следовательно,

.

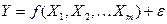Обычно предполагается, что случайная величина ( 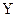) имеет нормальный закон распределения с условным математическим ожиданием 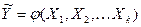и постоянной, не зависящей от аргументов дисперсией 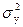. В анализе чаще всего используются уравнения регрессии линейного вида

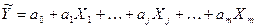
Коэффициенты регрессии 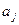показывают, на какую величину в среднем изменяется результативный признак 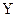, если независимая переменная 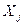, изменяется на единицу ее измерения.

В матричной форме регрессионная модель имеет вид

,

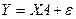где 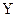– случайный вектор-столбец размерности ( 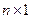) наблюдаемых значений результативного признака ( 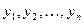); X – матрица размерности ( 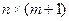) наблюдаемых значений аргументов. Элемент матрицы 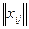рассматривается как неслучайная величина ( 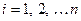; ; 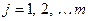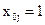); А – вектор-столбец размерности ( 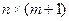)неизвестных параметров, подлежащих оценке в ходе регрессионного анализа (вектор коэффициентов регрессии); 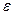- случайный вектор-столбец размерности ( 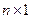) – вектор остатков, которые являются независимыми нормально распределенными случайными величинами с нулевым математическим ожиданием ( 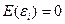) и неизвестной дисперсией .

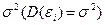На практике рекомендуется, чтобы число наблюдений (n)превышало число анализируемых признаков (m) не менее, чем в пять-шесть раз.

Для расчета вектора оценок коэффициентов регрессии 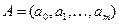по методу наименьших квадратов используется формула

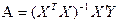, (2.4)

где

; ; ;

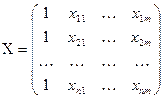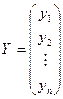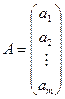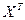
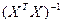
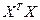
где

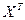– транспонированная матрица X;

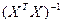– матрица, обратная матрице .

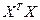Для устранения влияния различия дисперсий и единиц измерения отдельных переменных на результаты регрессионного анализа в ряде случаев целесообразно вместо исходных значений переменных 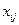использовать нормированные значения 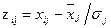. В этом случае уравнение множественной линейной регрессии будет иметь следующий вид:

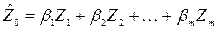(1.5)

где 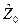– нормированное значения отклика ;

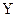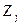– нормированные значения предикторов (независимых переменных – ,);

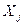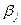— нормированные коэффициенты регрессии, которые могут быть вычислены исходя из следующей системы уравнений:

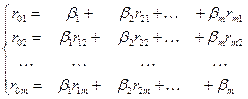
Если решать данную систему по правилу Крамера, т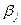о равно

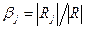, (2.6)

где 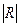– определитель матрицы системы уравнений;

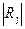– определитель матрицы системы линейных уравнений, в которой j-й столбец заменен столбцом свободных членов уравнений системы ( ).

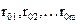Когда уравнение построено в нормированном масштабе, коэффициенты регрессии 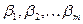показывают, за сколько нормированных отклонений изменится 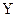при изменении каждой из 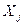на одно нормированное отклонение.

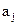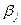Между коэффициентами и существует следующая зависимость:

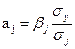. (2.7)

Кроме того, при помощи коэффициентов 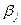можно рассчитать частный ( 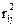) и множественный ( 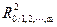)коэффициенты детерминации

;

,

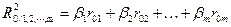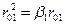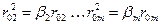
причем

.

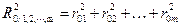После того как рассчитано само уравнение регрессии и перечисленные выше характеристики корреляционных связей, необходимо убедиться в адекватности полученных результатов.

Значимость уравнения регрессии в целом, т.е. нулевая гипотеза 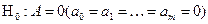, проверяется по F-критерию Фишера. Его наблюдаемое значение определяется по формуле

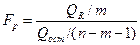, (2.8)

где ,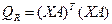

.

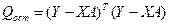По таблице распределения значений F-критерия Фишера, при заданных 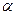, , 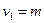,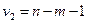находят 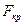.Гипотеза 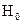отклоняется с вероятностью 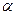, если 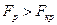. Из этого следует, что уравнение является значимым, т.е. хотя бы один из коэффициентов регрессии существенно отличен от нуля.

Для проверки значимости отдельных коэффициентов регрессии, т.е. гипотез 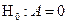, где 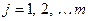, используют t-критерий Стьюдента, фактическое значение которого вычисляют следующим образом:

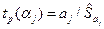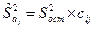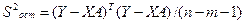; ; , (2.9)

где 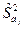– средняя ошибка коэффициента регрессии 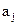, 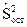– оценка среднего квадрата ошибки; 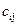– соответствующие коэффициенту 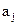диагональные элементы матрицы .

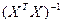По таблице значений t-критерия Стьюдента для заданного уровня значимости и числа степеней свободы ( 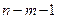) находят 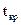. Значимость проверяемого коэффициента 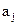подтверждается, если 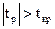. В противном случае коэффициент регрессии незначим, и соответствующая ему переменная не должна входить в модель.

Аналогичным образом осуществляется проверка значимости парных и частных коэффициентов корреляции. При этом табличное значение определяется для числа степеней свободы, равного ( 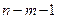), а расчетное значение критерия начисляется по формуле

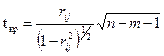. (2.10)

Значимость множественного коэффициента детерминации ( 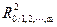) и соответственно множественного коэффициента корреляции ( 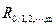) оценивается по F- критерию Фишера. Расчетное значение этого критерия определяется по формуле

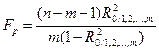. (2.11)

Гипотеза о значимости множественного коэффициента детерминации принимается в том случае, если 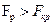для заданного уровня значимости 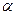и числа степеней свободы 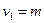, и .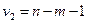

Пример. На основании приведенных данных таблицы 2.2 по районам области постройте линейную регрессионную модель валового выпуска продукции сельского хозяйства в целом по области.

Таблица 2.2

Район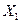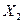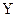
		12,22	121,0
		8,96	43,0
		11,69	69,0
		5,38	21,0
		8,66	58,0
		9,35	29,0
		8,92	66,0
		7,61	54,0
		11,32	86,0
		9,53	81,0
		6,75	52,0
		7,00	35,0
		6,58	27,0
		6,79	74,0
		9,12	83,0
		4,79	57,0

Здесь: 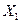– нагрузка пашни на одного работника, га; 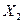– производительность труда одного работника, тыс. ден. ед.; 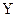– валовая продукция, млн. ден. ед.

1. Рассчитать уравнение множественной линейной регрессии.

2. Оценить тесноту связи между анализируемыми признаками с помощью коэффициентов корреляции и детерминации (парных и множественных).

3. Оценить значимость коэффициентов регрессии по t-критерию Стьюдента и качество модели по F-критерию Фишера. Поясните экономический смысл полученных результатов.

Решение.

1 Для оценки коэффициентов уравнения регрессии воспользуемся методом наименьших квадратов (МНК).

С этой целью строим систему нормальных уравнений для матрицы исходных значений переменных:

; ; ;

; ;

;

; .

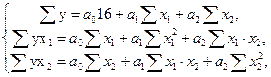
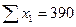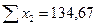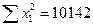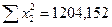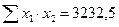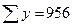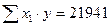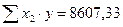Система уравнений будет иметь вид

; ; .

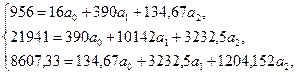
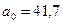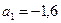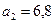Уравнение регрессии можно записать следующим образом:

.

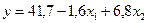Рассмотрим экономический смысл полученных коэффициентов регрессии для нашего примера. Первый коэффициент 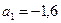показывает, что при увеличении нагрузки пашни на одного работника на 1 га объем выпуска продукции сельского хозяйства уменьшится на 1,6 млн. ден. ед. Второй коэффициент регрессии 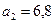показывает, что при увеличении производительности труда одного работника на 1 тыс. ден. ед., объем выпуска продукции увеличится на 6,8 млн. ден. ед. при прочих равных условиях.

2 Для расчетов коэффициентов корреляции и детерминации (парных и множественных) проведем, прежде всего, стандартизацию исходных переменныхи рассчитаем матрицу корреляций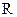

,

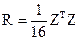где 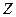– матрица стандартизованных значений переменных

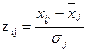
Матрица 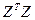будет иметь следующий вид:

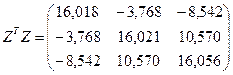, а матрица корреляций будет равна

.

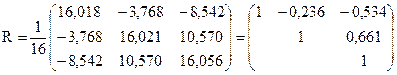Теперь рассчитаем множественный коэффициент детерминации (R²)и множественный коэффициент корреляции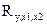

,

.

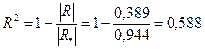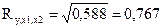Полученные результаты позволяют сделать следующий вывод: вариация объема выпуска продукции на 58,8 % зависит от исследуемых признаков-факторов; связь между результативным признаком (откликом) достаточно тесная, поскольку множественный коэффициент корреляции близок к единице .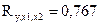

Пример. На основе приведенных данных таблицы 2.3 по десяти промышленным предприятиям проведите регрессионный анализ зависимости себестоимости произведенной продукции 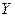(млн. ден. ед.) от объема произведенной продукции 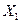(млн. ден. ед.) и уровня производительности труда рабочих 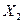(тыс. ден. ед. на человека).

Таблица 2.3

№ п/п		2'									Итого
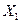	3,3	4,2	5,0	5,6	5,8	5,1	6,2	7,0	10,8	15,0
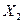	1,7	1,5	1,4	1,3	1,3	1,5	1,6	1,2	1,3	1,2
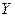	2,5	2,7	3,7	4,0	4,3	4,6	5,0	6,0	7,2	10,0

Решение.

1 Вектор оценок коэффициентов регрессии 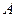определяется из уравнения

.

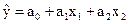Согласно методу наименьших квадратов, вектор 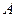расчитывается из выражения ,

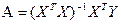где , , ;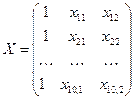

; .

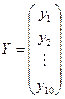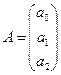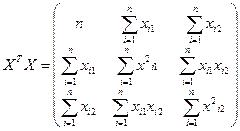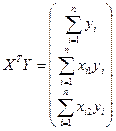Для того чтобы рассчитать все необходимые элементы матрицы 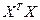вектора 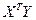заполним таблицу 2.4.

Таблица 2.4

№ п/п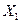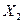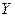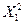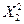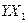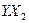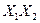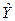
	3,3	1,7	2,5	10,89	2,89	8,25	4,25	5,61	2,59
	4,2	1,5	2,7	17,64	2,25	11,34	4,05	6,37	3,25
	5,0	1,4	3,7	25,00	1,96	18,50	5,18	7,0	3,79
	5,6	1,3	4,0	31,36	1,69	22,40	5,20	7,28	4,21
	5,8	1,3	4,3	33,64	1,69	24,94	5,59	7,54	4,32
	5,1	1,5	4,6	26,01	2,25	23,46	6,90	7,65	3,78
	6,2	1,6	5,0	38,44	2,56	31,00	8,00	9,92	4,35
	7,0	1,2	6,0	49,00	1,44	42,00	7,20	8,40	5,10
	10,8	1,3	7,2	116,64	1,69	77,76	9,36	14,04	7,26
	15,0	1,2	10,0	225,00	1,44	150,0	12,0	18,00	9,79
Итого				573,62	19,86	409,65	67,73	91,74	48,5

.

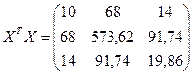
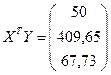Рассчитываем элементы обратной матрицы 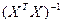и вектор оценок коэффициентов регрессии 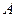.Определитель матрицы | 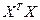|=169,456, а обратная матриц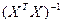а равна

,

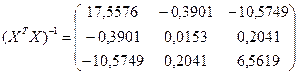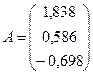
и оценку уравнения регрессии 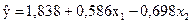. Получаем

.

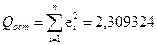
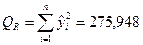Тогда несмещенная оценка остаточной дисперсии равна

,

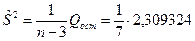а оценка среднеквадратического отклонения составит .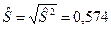

Проверяем на уровне значимости 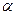=0,05 адекватность уравнения регрессии,т.е. гипотезу 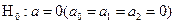. Для этого вычисляем наблюдаемое значение F-критерия

.

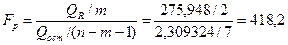По таблице F-распределения для заданного уровня значимости 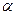=0,05 и числа степеней свободы 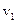=3 и 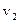=7 находим 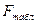=4,35.

Так как 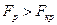(418,2>4,35), гипотеза отвергается с вероятностью ошибки 0,05. Таким образом, уравнение является значимым, т.е. хотя бы один из рассчитанных коэффициентов регрессии отличен от нуля.

Перед проверкой значимости отдельных коэффициентов регрессии найдем оценкуковариационной матрицы вектора коэффициентов регрессии ( ):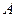

Учитывая, что на главной диагонали ковариационной матрицы находятся дисперсии коэффициентов регрессии, получаем следующие несмещенные оценки этих дисперсий:

( );

( );

( );

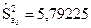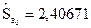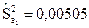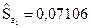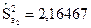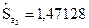и оценку корреляционной матрицы 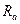с элементами, определяемыми по формуле

,

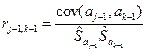где 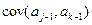– элементы матрицы 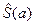, стоящие на пересечении j-строки и k-столбца, j, k=1,2,3.

Находим оценку корреляционной матрицы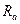

.

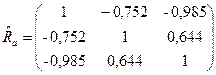Для проверки значимости отдельных коэффициентов регрессии, т.е. гипотез 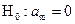, где 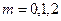находим по таблицам 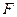-распределения для 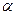=0,05, 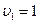, 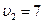критическое значение .

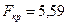Вычисляем 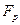для каждого и коэффициентов регрессии по формуле

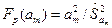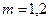, . Подставляя данные, получаем

; .

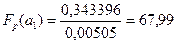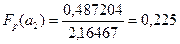Так как 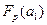> 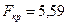, то коэффициент регрессии 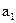значимо отличается от нуля. Для коэффициента 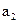выполняется неравенство 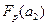< 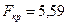, поэтому данный коэффициент можно считать незначимым.