Алгоритмы растровой графики
2.1. Растровые представления изображений.
Цифровое изображение – набор точек (пикселей) изображения; каждая точка изображения характеризуется координатами x и y и яркостью V(x,y), это дискретные величины, обычно целые. В случае цветного изображения, каждый пиксель характеризуется координатами x и y, и тремя яркостями: яркостью красного, яркостью синего и яркостью зеленого (VR , VB , VG). Комбинируя данные три цвета можно получить большое количество различных оттенков.
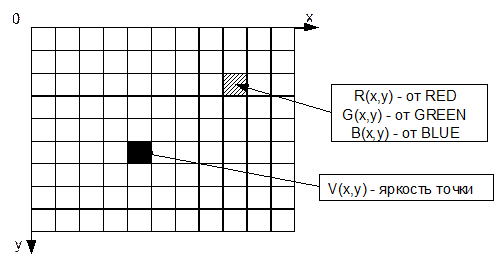
Рис. 2.1.1
Под градацию яркости обычно отводится 1 байт, причем 0 – черный цвет, а 255 – белый (максимальная интенсивность). В случае цветного изображения отводится по байту на градации яркостей всех трех цветов. Возможно кодирование градаций яркости другим количеством битов (4 или 12), но человеческий глаз способен различать только 8 бит градаций на каждый цвет, хотя специальная аппаратура может потребовать и более точную передачу цветов.
Цветовое пространство, образуемое интенсивностями красного, зеленого и синего, представляют в виде цветового куба.
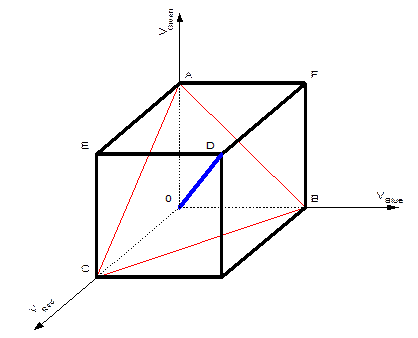
Рис. 2.1.2 «Цветовой Куб»
Вершины куба A, B, C являются максимальными интенсивностями зеленого, синего и красного соответственно, а треугольник которые они образуют называется треугольником Паскаля периметр этого треугольника соответствует максимально насыщенным цветам. На отрезке OD находятся оттенки серого, причем тока O соответствует черному, а точка D белому цвету.
Растр – это порядок расположения точек (растровых элементов). На рис. 2.1.1 изображен растр элементами которого являются квадраты, такой растр называется квадратным, именно такие растры наиболее часто используются. Хотя возможно использование в качестве растрового элемента фигуры другой формы, соответствующего следующим требованиям:
1. Все фигуры должны быть одинаковые;
2. Должны полностью покрывать плоскость без наезжания и дырок.
Так в качестве растрового элемента возможно использование равностороннего треугольника рис. 2.1.3, правильного шестиугольника (гексаэдра) рис. 2.1.4. Можно строить растры, используя неправильные многоугольники, но практический смысл в подобных растрах отсутствует.
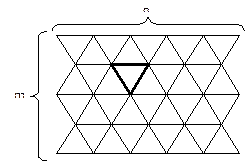
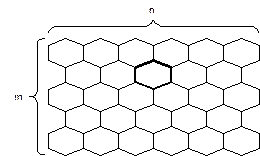
Рис. 2.1.3 «Треугольный растр» Рис. 2.1.4 «Гексагональный растр»
Рассмотрим способы построения линий в прямоугольном и гексагональном растре.
В квадратном растре построение линии осуществляется двумя способами:
1) Результат – восьмисвязная линия. Соседние пиксели линии могут находится в одном из восьми возможных (см. рис. 2.1.5а) положениях. Недостаток – слишком тонкая линия при угле 45°.
2) Результат – четырехсвязная линия. Соседние пиксели линии могут находится в одном из четырех возможных (см. рис. 2.1.5б) положениях. Недостаток – избыточно толстая линия при угле 45°.
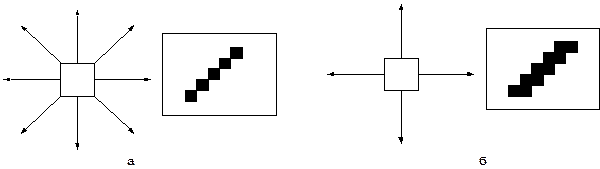
Рис. 2.1.5 «Построение линии в прямоугольном растре»
В гексагональном растре линии шестисвязные (см. рис. 2.1.6) такие линии более стабильны по ширине, т.е. дисперсия ширины линии меньше, чем в квадратном растре.

Рис. 2.1.6 «Построение линии в гексагональном растре»
Каким образом можно оценить, какой растр лучше?
Одним из способов оценки является передача по каналу связи кодированного, с учетом используемого растра, изображения с последующим восстановлением и визуальным анализом достигнутого качества. Экспериментально и математически доказано, что гексагональный растр лучше, т.к. обеспечивает наименьшее отклонение от оригинала. Но разница не велика.
