Методы построения алгоритмов

РЕКУРСИВНЫЕ МЕТОДЫ ПОСТРОЕНИЯ АЛГОРИТМОВ

Определение 6. Рекурсия – способ организации вычислительного процесса, при котором функция в ходе выполнения составляющих ее операторов обращается сама к себе.[7]

Использование рекурсии сокращает программу, в этом ее преимущество перед использованием итерационных циклов, но при выполнении может вызвать переполнение оперативной памяти компьютера.

Вид рекурсивной процедуры:

Рассмотрим типовой пример задачи вычисления факториала числа.

На рис. 13 показаны прямой и обратный ход рекурсии. [6] В любой рекурсивной подпрограмме обязательно должна быть не рекурсивная ветвь:

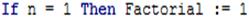
Пусть переменной a присваивается значение 5!:

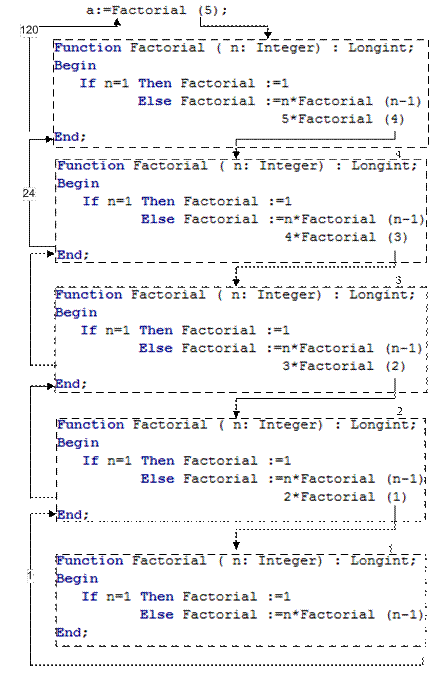
Рис. 13. Прямой и обратный ход рекурсии.

Рассмотрим некоторые примеры использования рекурсии.[6]

1. Сложение двух чисел a + b. Рекурсивное определение операции сложения двух чисел:

a + b =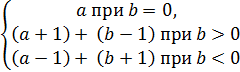

2. Каждое число Фибоначчи равно сумме двух предыдущих чисел при условии, что первые два равны 1 (1, 1, 2, 3, 5, 8, 13, 21,…).В общем виде n-e число Фибоначчи можно определить так:
Ф(n)=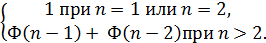

3. «Ханойские башни». В конце XIX века в Европе появилась игра под названием «Ханойские башни». Реквизит игры состоит из 3 игл, на которых размещается башня из колец. Цель игры – перенести башню с левой иглы (1) на правую (3), причем за один раз можно перенести только одно кольцо. Кроме того, запрещается помещать большее кольцо над меньшим.

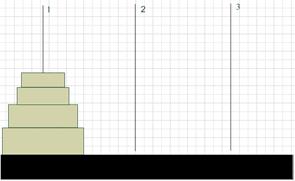
Программа, которая печатает последовательность переноса колец посредством рекурсивной процедуры, представлена в Приложении 1, Hanoy.pas.

Данная задача своим происхождением обязана легенде, в которой рассказывается, что в большом храме Бенареса на бронзовой плите установлены три алмазных стержня, на один из которых бог нанизал во время сотворение мира 64 золотых диска. С тех пор день и ночь монахи, сменяя друг друга каждую секунду, перекладывают по одному диску согласно описанным выше правилам. Конец мира наступит тогда, когда все 64 диска будут перемещены, на что потребуется чуть больше 58 млрд. лет.

МЕТОДЫ СОРТИРОВКИ ДАННЫХ

По методам сортировки, а также по методам поиска данных существует очень много публикаций. Рассмотрим основные методы сортировки данных ссылаясь на классическую книгу по программированию Кнут Д. «Искусство программирования», в которой методам сортировки посвящен третий том.

Сортировка простым выбором

Рассмотрим идею на примере. Пусть исходный массив А состоит из 10 элементов: 5 13 7 9 1 8 16 4 10 2. После сортировки массив должен выглядеть так: 1 2 4 5 7 8 9 10 13 16.

Процесс сортировки описан ниже. Максимальный элемент текущей части массива заключен в кружок, а элемент, с которым происходит обмен, в квадратик. Скобкой помечена рассматриваемая часть массива.

1-й шаг. Рассмотрим весь массив и найдем в нем максимальный элемент – 16 (на седьмом месте), поменяем его местами с последним элементом – с числом 2.

5 13 7 9 1 8 16 4 10 2

Максимальный элемент записан на свое место.

2-й шаг. Рассмотрим часть массива – с первого до девятого элемента. Максимальный элемент этой части – 13 (на втором месте). Поменяем его местами с последним элементом этой части – с числом 10.

5 13 7 9 1 8 2 4 10 16

Отсортированная часть массива имеет два элемента.

3-й шаг. Уменьшим рассматриваемую часть массива на один элемент. Здесь нужно поменять местами второй элемент (его значение – 10) и последний элемент этой части – число 4.

5 10 7 9 1 8 2 4 13 16

В отсортированной части массива – 3 элемента.

4-й шаг.

5 4 7 9 1 8 2 10 13 16

5-й шаг. Максимальный элемент этой части массива является последним в ней, поэтому его нужно оставить на старом месте.

5 4 7 2 1 8 9 10 13 16

6-й шаг.

5 4 7 2 1 8 9 10 13 16

7-й шаг.

5 4 1 2 7 8 9 10 13 16

8-й шаг.

2 4 1 5 7 8 9 10 13 16

9-й шаг.

2 1 4 5 7 8 9 10 13 16

На рис. 14. представлена блок-схема алгоритма сортировки простым выбором. Программа - Приложение 1, Vibor.pas.

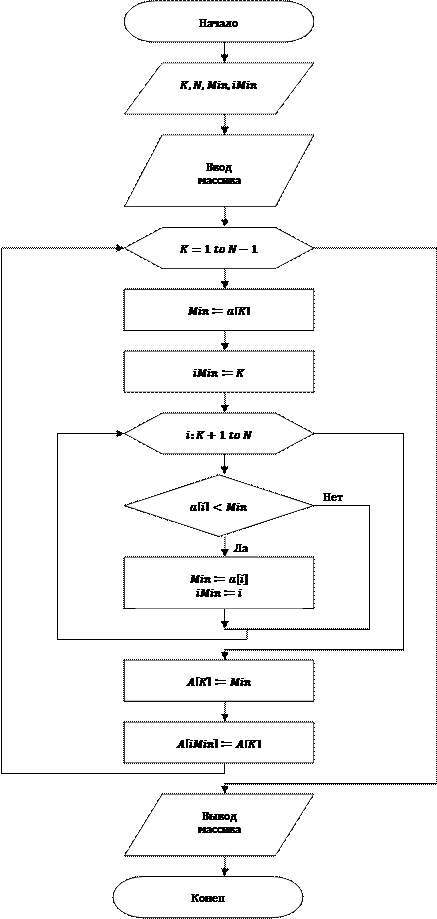
Рис. 14. Алгоритм сортировки методом выбора

2. Сортировка простым обменом. Метод «пузырька»

Рассмотрим идею метода на примере. Отсортируем по возрастанию массив из 5 элементов: 5 4 8 2 9. Длина текущей части массива – N-k+1, где k - номер просмотра, I – номер первого элемента проверяемой пары, номер последней пары – N-k.

Первый просмотр: рассматривается весь массив.

I=1 5 4 8 2 9

> меняем

I=2 4 5 8 2 9

< не меняем

I=3 4 5 8 2 9

> меняем

I=4 4 5 2 8 9

< не меняем

Цифра 9 находится на своем месте.

Второй просмотр:рассматриваем часть массива с первого до предпоследнего элемента.

I=1 4 5 2 8 9

< не меняем

I=2 4 5 2 8 9

> меняем

I=3 4 2 5 8 9

< не меняем

Цифра 8 на своем месте.

Третий просмотр:рассматриваемая часть массива содержит три первых элемента.

I=1 4 2 5 8 9

> меняем

I=2 2 4 5 8 9

< не меняем

Цифра 5 на своем месте.

Четвертый просмотр:рассматриваем последнюю пару элементов.

I=1 2 4 5 8 9

< не меняем

Цифра 4 на своем месте. Наименьший элемент – 2 оказывается на первом месте. Количество просмотров элементов массива равно N-1.

Итак, массив отсортирован. Этот метод также называют методом «пузырька», потому что при выполнении сортировки более «легкие» элементы (элементы с заданным свойством) постепенно всплывают на «поверхность».

На рис. 15. представлена блок-схема алгоритма сортировки методом «пузырька». Программа – Приложение 1, Puz.pas.

Сортировка простыми вставками.

Сортировка этим методом производится последовательно шаг за шагом. На 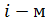шаге считается, что часть массива, содержащая первые 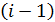элементов, уже упорядочена, то есть 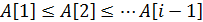. Далее следует взять 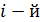элемент, и для него найти место в отсортированной части массива, такое, что после его вставки упорядоченность не нарушится, то есть требуется найти такое 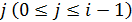, что 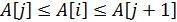, (при 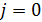происходит только одно сравнение). Затем выполняется вставка элемента 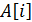на место 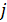. На каждом шаге отсортированная часть массива увеличивается. Для выполнения полной сортировки потребуется выполнить 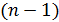шаг.

Рассмотрим этот процесс на примере. Таблица 3. Пусть требуется отсортировать массив из 10 элементов по возрастанию.

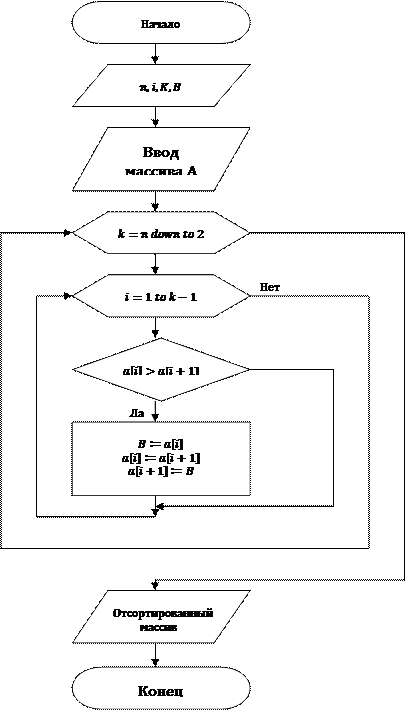
Рис. 15. Алгоритм сортировки методом «пузырька»

Таблица 3. Сортировка вставками

1-й шаг.	13 6 8 11 3 1 5 9 15 7	Рассматриваем часть массива из одного элемента 13. Вставляем второй элемент массива 6 так, чтобы упорядоченность сохранилась. Так как 6<13, записываем 6 на первое место. Отсортированная часть массива содержит два элемента (6 13).
2-й шаг.	6 13 8 11 3 1 5 9 15 7	Возьмем третий элемент массива 8 и подберем для него место в упорядоченной части массива. 8>6 и 8<13, следовательно, его место второе.
3-й шаг.	6 8 13 11 3 1 5 9 15 7	Следующий элемент – 11. Он записывается в упорядоченную часть массива на третье место, так как 11>8, но 11<13.
4-й шаг.	6 8 11 13 3 1 5 9 15 7	Далее, действуя аналогичным образом, определяем, что 3 необходимо записать на первое место.
5-й шаг.	3 6 8 11 13 1 5 9 15 7	По той же причине 1 записываем на первое место.
6-й шаг.	1 3 6 8 11 13 5 9 15 7	Так как 5>3, но 5<6, то место 5 в упорядоченной части – третье.
7-й шаг.	1 3 5 6 8 11 13 9 15 7	Место числа 9 – шестое.
8-й шаг.	1 3 5 6 8 9 11 13 15 7	Определяем место для предпоследнего элемента 15. оказывается, что этот элемент массива уже находится на своем месте.
9-й шаг.	1 3 5 6 8 9 11 13 15 7	Осталось подобрать подходящее место для последнего элемента 7.
	1 3 5 6 7 8 9 11 13 15	Массив отсортирован полностью.

Блок-схема алгоритма сортировки массива вставками на рис.16. Программа сортировки вставками представлена в Приложении 1, Vstavka.pas.

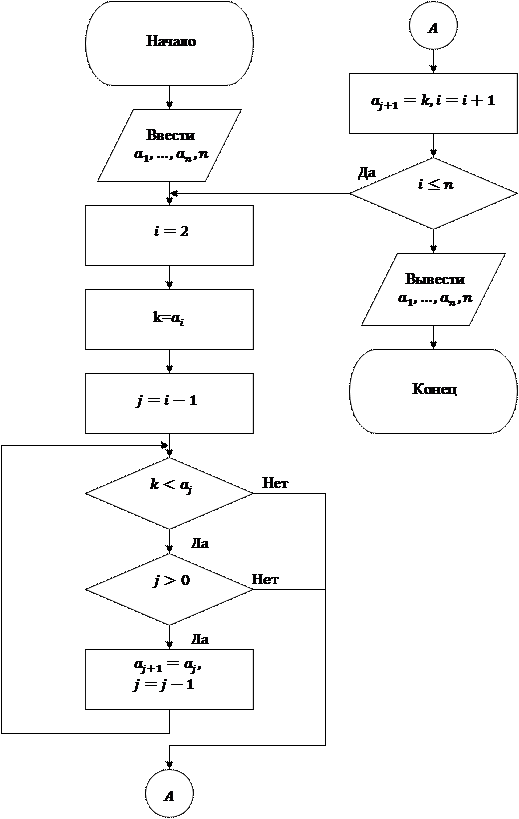
Рис.16 Алгоритм сортировки элементов массива вставками

Методы быстрой сортировки.

Метод сортировки слиянием.

Прежде, чем обсуждать метод, рассмотрим следующую задачу. Объединить («слить») упорядоченные фрагменты массива А A[k],…,A[m] и A[m+1],…,A[q] в один A[k],…,A[q], естественно, тоже упорядоченный (k 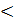m 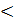q). Основная идея решения состоит в сравнении очередных элементов каждого фрагмента, выяснении, какой из элементов меньше, переносе его во вспомогательный массив D (для простоты) и продвижении по тому фрагменту массива, из которого взят элемент. При этом следует не забывать записать в D оставшуюся часть этого фрагмента, который не успел себя «исчерпать».

Рассмотрим сортировку массива методом слияния на примере.

Пример.Пусть первый фрагмент состоит из 5 элементов: 3 5 8 11 16, а второй – из 8: 1 5 7 9 12 13 18 20. Рисунок иллюстрирует логику объединения фрагментов.

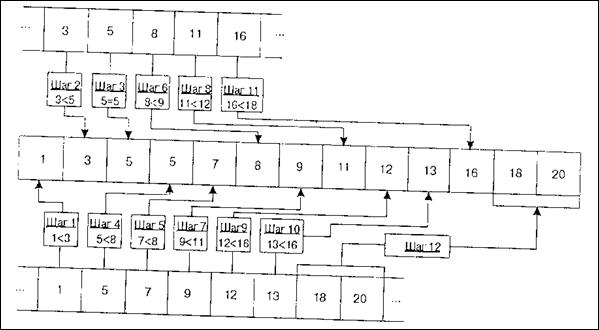
Рис. 17. Метод сортировки элементов массива слиянием

Программная реализация метода сортировки слиянием – Приложение 1, Slianie.pas.

Метод слияний – один из первых в теории алгоритмов сортировки. Он предложен Дж. фон Нейманом в 1945 году. Недостатком сортировки слиянием является использование дополнительной памяти. Но при работе с файлами или списками, доступ к которым осуществляется только последовательно, очень удобно применение этого метода.[6, 10]

Метод быстрой сортировки. Сортировка Хоара.

Метод предложен Ч. Э. Р. Хоаром в 1962 году. Эффективность метода достаточно высокая, поэтому автор назвал его «быстрой сортировкой».

Идея метода. В исходном массиве 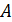выбирается некоторый элемент 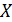(барьерный элемент). Следует записать 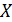«на свое место» в массиве, например, 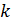, такое, что слева от 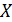были элементы массива, меньшие или равные 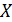, а справа – элементы массива, большие 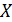, т.е. массив 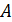будет иметь вид: .

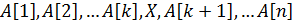В результате элемент 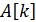находится на своем месте и исходный массив 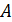разделен на две неупорядоченные части, барьером между которыми является элемент 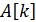. Далее сортируем полученные части по той же логике до тех пор, пока не останутся части массива, состоящие из одного элемента, то есть пока не будет отсортирован весь массив.

Рассмотрим сортировку массива методом Хоара на примере.[6,10]

Пример.Исходный массив состоит из 8 элементов: 8 12 3 7 19 11 4 16. В качестве барьерного элемента возьмем средний элемент массива (7).

Произведя необходимые перестановки, получим: (4 3) 7 (12 19 11 8 16), элемент 7 находится на своем месте. Продолжим сортировку.

Левая часть: (3) 4 7 (12 19 11 8 16)

3 4 7 (12 19 11 8 16)

Правая часть:

3 4 7 (8) 11 (19 12 16)

3 4 7 8 11 (19 12 16)

3 4 7 8 11 12 (19 16)

3 4 7 8 11 12 (16) 19

3 4 7 8 11 12 16 19

Из вышеизложенного описания явно просматривается рекурсивная схема реализации, параметрами которой являются нижняя и верхняя границы изменения индексов сортируемой части исходного массива. Приведем процедуру быстрой сортировки. [7]

Procedure QuickSort (m, t : Integer); {*m- начало массива, t – конец массива.*}

Var i, j, x, w : Integer;

Begin

I:=m; j:=t; x:=A [(m+t) Div 2];

Repeat

While A[i] < x Do Inc (i);

While A[j] > x Do Dec (j);

If i<=j Then Begin w:=A[i]; A[i]:=A[j]; A[j]:=w;

Inc (i); Dec (j); End

Until i>j;

If m<j Then QuickSort (m, j);

If i<t Then QuickSort (I, t);

End;