Построение эмпирических формул методом наименьших квадратов

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Тема: Реализация численного метода средствами Microsoft Excel и с помощью средств среды программирования Visual Basic 6.0

Автор: студент гр. СТ-11 __________________ /Максимова Е. Н./ ^{(шифр группы) (подпись) (Ф.И.О.)}

ОЦЕНКА: _____________

Дата: _____________

ПРОВЕРИЛ:

Руководитель работы _________ ____________ /Алейников А.А./

^{(должность) (подпись) (Ф.И.О.)}

Санкт-Петербург

Министерство образования и науки Российской Федерации
Национальный минерально-сырьевой университет "Горный"
		УТВЕРЖДАЮ Заведующий кафедрой   /_____________/ доц. Маховиков А.Б./   "___"__________2012 г.

Кафедра: __________Информатики и компьютерных технологий_______________

КУРСОВАЯ РАБОТА

по дисциплине __________________ИНФОРМАТИКА________________________

^{(наименование учебной дисциплины согласно учебному плану)}

ЗАДАНИЕ

студенту группы СТ-11Максимовой Е.Н.

^{(шифр группы) (Ф.И.О.)}

1. Тема работы: _Реализация численного метода средствами Microsoft Excel и с помощью среды программирования Visual Basic 6.0

2. Исходные данные к работе: _Вариант № 14__________________________________

_________

3. Содержание пояснительной записки: _Пояснительная записка включает в себя задание на выполнение работы, расчетные формулы, расчет с помощью таблиц (Microsoft Excel), результаты расчета, расчет с использованием среды программирования Visual Basic 6.0, результаты расчета, графики, заключение, библиографический список____

4. Перечень графического материала: _Представление результатов в виде экранных форм____________________________________________________________________

5. Срок сдачи законченной работы: ___01.12.2012 г.____________________________

Руководитель работы: ________ ______________ /Алейников А.А./

^{(должность) (подпись) (Ф.И.О.)}

Дата выдачи задания: __15.09.2012 г.______________

Содержание

С.

Аннотация. 4

Аппроксимация функции методом наименьших квадратов. 5

Введение. 5

1 Построение эмпирических формул методом наименьших квадратов. 5

2 Процесс решения поставленной задачи с помощью табличного процессора Microsoft Excel 10

3 Реализация решения поставленной задачи с помощью среды программирования Visual Basic 6.0. 22

Заключение. 31

Библиографический список. 32

Аннотация

Пояснительная записка представляет собой отчет о выполнении курсовой работы. В ней рассматриваются вопросы по нахождению эмпирических формул методом наименьших квадратов (МНК) посредством возможностей пакета Microsoft Excel, а также рассматривается решение данной с помощью среды программирования Visual Basic 6.0. В работе получены уравнения различных видов с помощью аппроксимации линейной, квадратичной и экспоненциальной зависимостей. По окончании работы сделан вывод, каким методом задача решена лучше всего.

Страниц 32, таблиц 11, рисунков 8

Abstract

The explanatory note represents the report on term paper performance. In it questions on a finding of empirical formulas by a method of the least squares (МНК) by means of possibilities of package Microsoft Excel are considered, and also the decision of the given problem in Visual Basic 6.0 is considered. In work the equations of various kinds by means of approximation linear, square-law and экспоненциальной dependences are received. Upon termination of work the conclusion is drawn, the problem is solved by what method is better.

Pages 32, tables 11, figures 8, appendixes

Аппроксимация функции методом наименьших квадратов

Введение

Целью выполнения курсовой работы является развитие и закрепление навыков работы с табличным процессором Microsoft Excel и визуальной средой программирования Visual Basic 6.0, изучаемых в курсе информатики, и их применение с помощью компьютера для самостоятельного решения задач из предметной области, связанной с исследованиями.

Отчет представляется в виде записки. Порядок изложения материала следующий:

- задание;

- расчетные формулы;

- таблицы, выполненные средствами Microsoft Excel, с пояснениями;

- результаты обработки заданных экспериментальных данных с использованием средств среды программирования Visual Basic 6.0;

- выводы;

- библиографический список.

Построение эмпирических формул методом наименьших квадратов

Очень часто, особенно при анализе эмпирических данных возникает необходимость найти в явном виде функциональную зависимость между величинами x и y , которые получены в результате измерений.

При аналитическом исследовании взаимосвязи между двумя величинами x и y производят ряд наблюдений, и в результате получается таблица значений:

			…		…
			…		…

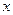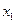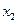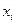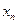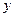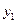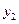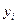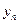Эта таблица обычно получается как итог каких-либо экспериментов, в которых 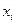(независимая величина) задается экспериментатором, а 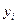получается в результате опыта. Поэтому эти значения 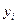будем называть эмпирическими или опытными значениями.

Между величинами x и y существует функциональная зависимость, но ее аналитический вид обычно неизвестен, поэтому возникает практически важная задача – найти эмпирическую формулу

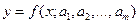, (1)

(где 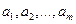- параметры), значения которой при 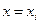мало отличались бы от опытных значений .

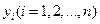Обычно указывают класс функций (например, множество линейных, степенных, показательных и т.п.), из которого выбирается функция 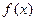, и далее определяются наилучшие значения параметров.

Если в эмпирическую формулу (1) подставить исходные значения 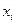, то получим теоретические значения 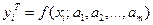, где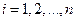

Разности 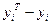называются отклонениями и представляют собой расстояния по вертикали от точек 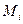до графика эмпирической функции.

Согласно методу наименьших квадратов наилучшими коэффициентами 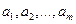считаются те, для которых сумма квадратов отклонений найденной эмпирической функции от заданных значений функции равна

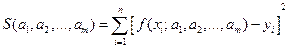(2)

и будет минимальной.

Поясним геометрический смысл метода наименьших квадратов.

Каждая пара чисел 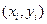из исходной таблицы определяет точку 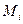на плоскости XOY . Используя формулу (1) при различных значениях коэффициентов 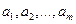можно построить ряд кривых, которые являются графиками функции (1). Задача состоит в определении коэффициентов 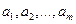таким образом, чтобы сумма квадратов расстояний по вертикали от точек 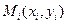до графика функции (1) была наименьшей (рис.1).

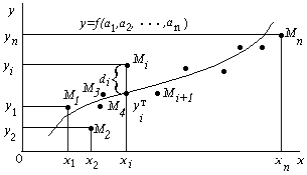
Рис.1

Построение эмпирической формулы состоит из двух этапов:

- выяснение общего вида этой формулы;

- определение ее наилучших параметров.

Если неизвестен характер зависимости между данными величинами x и y , то вид эмпирической зависимости является произвольным. Предпочтение отдается простым формулам, обладающим хорошей точностью. Удачный выбор эмпирической формулы в значительной мере зависит от знаний исследователя в предметной области, используя которые он может указать класс функций из теоретических соображений. Большое значение имеет изображение полученных данных в декартовых или в специальных системах координат (полулогарифмической, логарифмической и т.д.). По положению точек можно примерно угадать общий вид зависимости путем установления сходства между построенным графиком и образцами известных кривых.

Определение наилучших коэффициентов 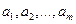входящих в эмпирическую формулу производят хорошо известными различными аналитическими методами.

Для того чтобы найти набор коэффициентов 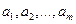, которые доставляют минимум функции S , определяемой формулой (2), используем необходимое условие экстремума функции нескольких переменных, а именно равенство нулю частных производных. В результате получим нормальную систему для определения коэффициентов :

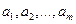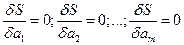(3)

Таким образом, нахождение коэффициентов 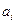сводится к решению системы (3).

Эта система упрощается, если эмпирическая формула (1) линейна относительно параметров 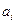, тогда система (3) будет линейной.

Конкретный вид системы (3) зависит от того, из какого класса эмпирических формул мы ищем зависимость (1). В случае линейной зависимости 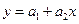система (3) примет вид:

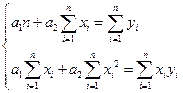(4)

Эта линейная система может быть решена любым известным методом (методом Гаусса, простых итераций, формулами Крамера).

В случае квадратичной зависимости 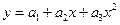система (3) примет вид:

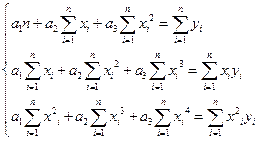(5)