Передача аргументов в функцию
В языке Си аргументы при стандартном вызове функции передаются по значению. Это означает, что в стеке, как и в случае локальных данных, выделяется место для формальных параметров функции. В выделенное место при вызове функции заносятся значения фактических аргументов, при этом проверяется соответствие типов и при необходимости выполняются их преобразования. При несоответствии типов выдается диагностическое сообщение. Затем функция использует и может изменять эти значения в стеке.
При выходе из функции измененные значения теряются, т.к. время жизни и зона видимости локальных параметров определяется кодом функции. Вызванная функция не может изменить значения переменных, указанных как фактические аргументы при обращении к данной функции.
В случае необходимости функцию можно использовать для изменения передаваемых ей аргументов. В этом случае в качестве аргумента необходимо в вызываемую функцию передавать не значение переменной, а ее адрес.
При передаче по адресу в стек заносятся копии адресов аргументов, а функция осуществляет доступ к ячейкам памяти по этим адресам и может изменить исходные значения аргументов. Для обращения к значению аргумента-оригинала используется операция «*».
Пример функции, в которой меняются местами значения x и y:
void zam(int *x, int *y)
{
int t = *x;
*x = *y;
*y = t;
}
Участок программы с обращением к данной функции:
void zam (int*, int*);
void main (void)
{
int a=2, b=3;
printf(" a = %d , b = %d\n", a, b);
zam (&a, &b);
printf(" a = %d , b = %d\n", a, b);
}
При таком способе передачи данных в функцию их значения будут изменены, т.е. на экран монитора будет выведено
a = 2 , b=3
a = 3 , b=2
Если требуется запретить изменение значений какого-либо параметра внутри функции, то в его декларации используют атрибут const, например:
void f1(int, const double);
Рекомендуется указывать const перед всеми параметрами, изменение которых в функции не предусмотрено. Это облегчает, например, отладку программы, т.к. по заголовку функции видно, какие данные в функции изменяются, а какие нет.
Операция typedef
Любому типу данных, как стандартному, так и определенному пользователем, можно задать новое имя с помощью операции typedef:
typedef тип новое_имя ;
Введенный таким образом новый тип используется аналогично стандартным типам, например, введя пользовательские типы:
typedef unsigned int UINT; – здесь UINT – новое имя;
typedef char M_s [101]; – здесь M_s – тип пользователя, определяющий строки, длиной не более 100 символов.
Декларации объектов введенных типов будут иметь вид
UINTi, j; ® две переменные типа unsigned int ;
M_s str[10]; ® массив из 10 элементов, в каждом из которых можно хранить по 100 символов.
Рассмотренная операция упростит использование указателей на функции, которые рассматриваются в следующем разделе.
Указатели на функции
В языке Си идентификатор функции является константным указателем на начало функции в оперативной памяти и не может быть значением переменной. Но имеется возможность декларировать указатели на функции, с которыми можно обращаться как с переменными (например, можно создать массив, элементами которого будут указатели на функции).
Рассмотрим методику работы с указателями на функции.
1. Как и любой объект языка Си, указатель на функции необходимо декларировать. Формат объявления указателя на функции следующий:
тип (*переменная-указатель)(список параметров);
т.е. декларируется указатель, который можно устанавливать на функции, возвращающие результат указанного типа и которые имеют указанный список параметров. Наличие первых круглых скобок обязательно, так как без них – это декларация функции, которая возвращает указатель на результат.
Например, объявление вида
double (*p_f )(char, double);
говорит о том, что декларируется указатель p_f, который можно устанавливать на функции, возвращающие результат типа double и имеющие два параметра: первый – символьного типа, а второй – вещественного типа.
2. Идентификатор функции является константным указателем, поэтому для того чтобы установить переменную-указатель на конкретную функцию, достаточно ей присвоить ее идентификатор:
переменная-указатель = ID_функции;
Например, имеется функция с прототипом: double f1(char, double); тогда операция
p_f = f1;
установит указатель p_f на данную функцию.
3. Вызов функции после установки на нее указателя выглядит так:
(*переменная-указатель)(список аргументов);
или
переменная-указатель (список аргументов);
После таких действий кроме стандартного обращения к функции:
ID_функции(список аргументов);
появляется еще два способа вызова функции:
(*переменная-указатель)(список аргументов);
или
переменная-указатель (список аргументов);
Последняя запись справедлива, так как p_f также является адресом начала функции в оперативной памяти.
Для нашего примера к функции f1 можно обратиться следующими способами:
f1(‘z’, 1.5); – обращение к функции по имени (ID);
(* p_f)(‘z’, 1.5); – обращение к функции по указателю;
p_f(‘z’, 1.5); – обращение к функции по ID указателя.
Основное назначение указателей на функции – это обеспечение возможности передачи идентификаторов функций в качестве параметров в функцию, которая реализует некоторый вычислительный процесс, используя формальное имя вызываемой функции.
Пример: написать функцию вычисления суммы sum, обозначив слагаемое формальной функцией fun(x). При вызове функции суммирования передавать через параметр реальное имя функции, в которой задан явный вид слагаемого. Например, пусть требуется вычислить две суммы:
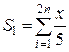 и
и 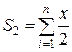 .
.
Поместим слагаемые этих сумм в пользовательские функции f1 и f2 соответственно. При этом воспользуемся операцией typedef, введя пользовательский тип данных: указатель на функции p_f, который можно устанавливать на функции, возвращающие результат double и имеющие один параметр типа double.
Тогда в списке параметров функции суммирования достаточно будет указать фактические идентификаторы функций созданного типа p_f.
Текст программы для решения данной задачи может быть следующим:
. . .
typedef double (*p_f)(double);
double sum(p_f, int, double); // Декларации прототипов функций
double f1(double);
double f2(double);
void main(void)
{
double x, s1, s2;
int n;
puts (" Введите кол-во слагаемых n и значение x: ");
scanf (" %d %lf ", &n, &x);
s1 = sum (f1, 2*n, x);
s2 = sum (f2, n, x);
printf("\n\t N = %d , X = %lf ", n, x);
printf("\n\t Сумма 1 = %lf\n\t Сумма 2 = %lf ", s1, s2);
}
/* Первый параметр функции суммирования – формальное имя функции, введенное с помощью typedef типа */
double sum(p_f fun, int n, double x) {
double s=0;
for(int i=1; i<=n; i++)
s+=fun(x);
return s;
}
//–––––––––––––– Первое слагаемое –––––––––––––––––––
double f1(double r) {
return r/5.;
}
//–––––––––––––– Второе слагаемое ––––––––––––––––––––
double f2(double r) {
return r/2.;
}
В заключение рассмотрим оптимальную передачу в функции одномерных и двухмерных массивов.
Передача в функцию одномерного массива:
void main(void)
{
int vect[20];
…
fun(vect);
…
}
void fun( int v[ ]) {
…
}
При использовании в качестве параметра одномерного массива в функцию передается указатель на его первый элемент, т.е. массив всегда передается по адресу и параметр v[ ] преобразуется в *v. Поэтому этой особенностью можно воспользоваться сразу:
void fun( int *v) {
…
}
При этом информация о количестве элементов массива теряется, так как размер одномерного массива недоступен вызываемой функции. Данную особенность можно обойти несколькими способами. Например, передавать его размер через отдельный параметр. Если же размер массива является константой, можно указать ее и при описании формального параметра, и в качестве границы циклов при обработке массива внутри функции:
void fun( int v[20]) {
. . .
}
В случае передачи массива символов, т.е. строки, ее фактическую длину можно определить по положению признака окончания строки (нуль-символа) через стандартную функцию strlen.
Передача в функцию двухмерного массива:
Если размеры известны на этапе компиляции, то
void f1(int m[3][4]) {
int i, j;
for ( i = 0; i<3; i++)
for ( j = 0; j<4; j++)
. . . // Обработка массива
}
Двухмерный массив, как и одномерный, также передается как указатель, а указанные размеры используются просто для удобства записи. При этом первый размер массива не используется при поиске положения элемента массива в ОП, поэтому передать массив можно так:
void main(void)
{
int mas [3][3]={{1,2,3}, {4,5,6}};
…
fun (mas);
…
}
void fun( int m[ ][3]) {
…
}
Если же размеры двухмерного массива, например, вводятся с клавиатуры (неизвестны на этапе компиляции), то их значения следует передавать через дополнительные параметры, например:
…
void fun( int**, int, int);
void main()
{
int **mas, n, m;
...
fun (mas, n, m);
…
}
void fun( int **m, int n, int m) {
. . . // Обработка массива
}
Рекурсивные функции
Рекурсивной (самовызываемой или самовызывающей) называют функцию, которая прямо или косвенно вызывает сама себя.
При каждом обращении к рекурсивной функции создается новый набор объектов автоматической памяти, локализованных в коде функции.
Возможность прямого или косвенного вызова позволяет различать прямую или косвенную рекурсии. Функция называется косвенно рекурсивной в том случае, если она содержит обращение к другой функции, содержащей прямой или косвенный вызов первой функции. В этом случае по тексту определения функции ее рекурсивность (косвенная) может быть не видна. Если в функции используется вызов этой же функции, то имеет место прямая рекурсия, т.е. функция по определению рекурсивная.
Рекурсивные алгоритмы эффективны в задачах, где рекурсия использована в самом определении обрабатываемых данных. Поэтому изучение рекурсивных методов нужно проводить, вводя динамические структуры данных с рекурсивной структурой. Рассмотрим вначале только принципиальные возможности, которые предоставляет язык Си для организации рекурсивных алгоритмов.
В рекурсивных функциях необходимо выполнять следующие правила.
1. При каждом вызове в функцию передавать модифицированные данные.
2. На каком-то шаге должен быть прекращен дальнейший вызов этой функции, это значит, что рекурсивный процесс должен шаг за шагом упрощать задачу так, чтобы для нее появилось нерекурсивное решение, иначе функция будет вызывать себя бесконечно.
3. После завершения очередного обращения к рекурсивной функции в вызывающую функцию должен возвращаться некоторый результат для дальнейшего его использования.
Пример 1. Заданы два числа a и b, большее из них разделить на меньшее, используя рекурсию.
Текст программы может быть следующим:
. . .
double proc(double, double);
void main (void)
{
double a,b;
puts(“ Введи значения a, b : ”);
scanf(“%lf %lf”, &a, &b);
printf(“\n Результат деления : %lf”, proc(a,b));
}
//––––––––––––––––––– Функция –––––––––––––––––––––––
double proc( double a, double b) {
if ( a< b ) return proc ( b, a );
else return a/b;
}
Если a больше b, условие, поставленное в функции, не выполняется и функция proc возвращает нерекурсивный результат.
Пусть теперь условие выполнилось, тогда функция proc обращается сама к себе, аргументы в вызове меняются местами и последующее обращение приводит к тому, что условие вновь не выполняется и функция возвращает нерекурсивный результат.
Пример 2. Функция для вычисления факториала неотрицательного значения k (для возможных отрицательных значений необходимо добавить дополнительные условия).
double fact (int k) {
if ( k < 1 ) return 1;
else
return k * fact ( k – 1);
}
Для нулевого значения параметра функция возвращает 1 (0! = 1), в противном случае вызывается та же функция с уменьшенным на 1 значением параметра и результат умножается на текущее значение параметра. Тем самым для значения параметра k организуется вычисление произведения
k * (k–1) * (k–2) * ... * 3 * 2 * 1 * 1
Последнее значение «1» – результат выполнения условия k < 1 при k = 0, т.е. последовательность рекурсивных обращений к функции fact прекращается при вызове fact(0). Именно этот вызов приводит к последнему значению «1» в произведении, так как последнее выражение, из которого вызывается функция, имеет вид: 1 * fact( 1 – 1).
Пример 3. Рассмотрим функцию определения корня уравнения f(x) = 0 на отрезке [а, b] с заданной точностью eps. Предположим, что исходные данные задаются без ошибок, т.е. eps > 0, f(a)*f(b) < 0, b > а, и вопрос о возможности существования нескольких корней на отрезке [а,b] нас не интересует. Не очень эффективная рекурсивная функция для решения поставленной задачи приведена в следующей программе:
. . .
int counter = 0; // Счетчик обращений к тестовой функции
//–––––––– Нахождение корня методом деления отрезка пополам ––––––––––
double Root(double f(double), double a, double b, double eps) {
double fa = f(a), fb = f(b), c, fc;
if ( fa * fb > 0) {
printf("\n На интервале a,b НЕТ корня!");
exit(1);
}
с = (а + b) / 2.0;
fc = f(c);
if (fc == 0.0 || fabs(b – a) < = eps) return c;
return (fa * fс < 0.0) ? Root(f, a, c, eps) : Root(f, c, b, eps);
}
//–––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––
void main()
{
double x, a=0.1, b=3.5, eps=5е–5;
double fun(double) ; // Прототип тестовой функции
x = Root (fun, a, b, eps) ;
printf ("\n Число обращений к функции = %d . ", counter);
printf ("\n Корень = %lf . ", x);
}
//–––––––––––––– Определение тестовой функции fun –––––––––––––––––
double fun (double x) {
counter++; // Счетчик обращений – глобальная переменная
return (2.0/x * соs(х/2.0));
}
Значения a, b и eps заданы постоянными только для тестового анализа полученных результатов, хотя лучше данные вводить с клавиатуры.
В результате выполнения программы с определенными в ней конкретными данными получим:
Число обращений к функции = 54 .
Корень = 3.141601.
Неэффективность предложенной программы связана, например, с излишним количеством обращений к программной реализации функции, для которой определяется корень. При каждом рекурсивном вызове функции Root повторно вычисляются значения f(a) и f(b), хотя они уже известны после предыдущего вызова.
В литературе по программированию рекурсиям уделено достаточно внимания как в теоретическом плане, так и в плане рассмотрения механизмов реализации рекурсивных алгоритмов. Сравнивая рекурсию с итерационными методами, отмечают, что рекурсивные алгоритмы наиболее пригодны в случаях, когда поставленная задача или используемые данные определены рекурсивно. В тех случаях, когда вычисляемые значения определяются с помощью простых рекуррентных соотношений, гораздо эффективнее применять итерационные методы.
Таким образом, рассмотренные выше примеры только иллюстрируют схемы организации рекурсивных функций, но не являются примерами эффективного применения рекурсивного подхода к вычислениям.
При обработке динамических информационных структур, которые включают рекурсивность в само определение обрабатываемых данных, применение рекурсивных алгоритмов не имеет конкуренции со стороны итерационных методов.
