В отчете (раздел «Способ решения поставленной задачи») должны быть представлены в развернутой форме построенные задачи с числовыми коэффициентами

Литература

1. Венцель Е.В. Исследование операций. М.: Сов. Радио, 1972.

ЗАДАНИЕ

ОПТИМАЛЬНЫЙ ПЛАН

при ограничениях на оборудование.

ЧАСТЬ 1. Составить задачу и решить

Производство с пятью видами продукции.

1. Провести расчет оптимального плана выпуска продукции в соответствии с приводимыми далее числовыми данными. Провести при заданном критерии исследование плана на устойчивость и пределы изменения коэффициентов, параметрический анализ.

2. Расчет провести в электронной таблице Excel.

3. В качестве критериев (целевых функций) оптимизации использовать максимизацию прибыли (критерий 1- кр1).

4. Исходные данные.

Предприятие выпускает изделия И1 – И5. Для этого используются следующие станки (оборудование).

1. Фрезерное с ресурсом В1 нормо-часов в месяц.

2. Токарное – с ресурсом В2.

3. Штамповочное – с ресурсом В3.

4. Сборочно-наладочное – с ресурсом В4.

5.. Поставляются комплектующие в количестве В5 штук в месяц.

Числовые данные характеризуются следующими таблицами.

Нормы расходов

Ресурсы	Изделия
И1	И2	И3	И4	И5
Фрезерное	15,4	13,3	18,2	16,1	14,0
Токарное	7,1	10,2	5,3	6,4	8,0
Штамповочное	0,14	0,19	0,17	0,15	0,19
Сборка	2,1	1,4	2,2	2,7	1,8
Комплектующие

Цена и себестоимость

	Изделия
И1	И2	И3	И4	И5
Цена
Себестоимость	s1	s2	s3	s4	s5

Ограничения на выпуск

	Изделия
И1	И2	И3	И4	И5
Минимум
Максимум

Соотношение количества выпускаемых изделий И2/И4=1/2.

Варианты заданий

Параметры	Варианты
В1
В2
В3
В4
В5
S1
Y1
Y2
Y3
S2
S3
S4
S5
T
В6

Результат представить и в виде таблицы

Критерий	И1	И2	И3	И4	И5
Кр. 1

Результат запомнить, поскольку он потребуется далее

ЧАСТЬ 2. Определение чувствительности параметрической решений.

В условиях части 1 исследовать устойчивость решения, для чего выполнить такие расчеты..

4.1. Исследовать границы изменений коэффициентов в ограничениях и целевой функции. Определить объем использованных ресурсов, резервы, двойственные переменные. Выявить наиболее дефицитный ресурс, близкий по значению к оптимальному вид продукции, наиболее и наименее чувствительные виды ресурсов.

Предположительные формы выходных документов на дополнительном листе Excel после решения задачи.

Продукция

Вид продукции	Оптимальный план	Двойственная переменная	Верхняя граница целевой функции	Нижняя граница целевой функции

Ресурсы

Вид ресурса	Объем используемого ресурса	Резерв ресурса	Двойственная оценка	Верхняя граница ресурса	Нижняя граница ресурса

Сделать выводы.

4.2. Исследовать результаты изменения значений коэффициентов:

а) целевой функции для первого и третьего изделий – на – 10 процентов;

б) целевой функции для второго и четвертого изделий – на –+10 процентов;

в) свободных членов для первого и третьего ограничений – на – 10 процентов;

г) свободных членов для второго и четвертого ограничений – на –+10 процентов;

д) коэффициентов для первого и третьего видов изделий – на – 10 процентов для третьего ресурсного ограничения;

е) коэффициентов для второго и четвертого видов изделий – на – 10 процентов для третьего ресурсного ограничения;

ж) коэффициентов для первого и третьего видов ресурсов – на – 10 процентов для пятого изделия;

и) коэффициентов для второго и четвертого видов ресурсов – на – 10 процентов для пятого изделия.

Полученные результаты свести в таблицу вида

Пункт	И1	И2	И3	И4	И5
4.2, а
4,2, б
……
4.2, и

Сделать выводы.

ЧАСТЬ 3. Многокритериальная (векторная) задача статического линейного программирования.

Для оптимального программирования (планирования) с одной целевой функцией (скалярным критерием) характерны следующие обстоятельства:

1) выбор вида целевой функции ­ процедура неформальная и неоднозначная;

2) вид целевой функции существенно влияет на характер функционирования системы;

3) использование только одного критерия характеризуется получением «крайних» решений, не учитывающих в достаточной мере факторов, наблюдающихся в реальной системе.

Для «сглаживания» этих крайностей используется векторная целевая функция (многокритериальная постановка задачи).

В качестве составляющих векторного критерия могут быть выбраны прибыль; доход; объем (выпуск) товарной продукции в оптовых ценах; нормативно-чистая продукция; производительность труда; рентабельность; фондоотдача; удельные затраты на выпуск продукции; объем и стоимость незавершенного производства; себестоимость. Независимо от выбора критериев формально в линейном варианте они различаются коэффициентами (весами) a_l при целевых функциях.

Нахождение решений при векторной целевой функции математически существенно усложняется и связывается с определением равновесия по Парето.

Полученные ранее оптимальные значения решений x (планов P) вычислены для скалярных целевых функций. Не снижая общности, считаем их первыми (l = 1) в векторных целевых функциях в задаче

AP £ b(0), b(0) = b₀, (4.9)

G_l(P) = C_lP à max, l = 1, L,

и обозначим через Р₁^*.

Аналогично решаются задачи для критериев G_l(Р^*) для l = 2, L и получаются значения Р_l^*. Результаты решения векторной задачи в значительной мере определяются самой неформальной постановкой задачи (схемой компромисса) – переходом от векторного критерия к скалярному.

Учет L критериев возможен двумя основными группами способов, сводящимися в конечном итоге к сворачиванию векторного критерия G_l к скалярному G через веса a_l:

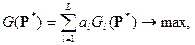
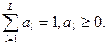(4.10)

Возможны следующие группы методов решения векторной задачи:

1) веса критериев заданы (назначены) экспертами априорно до решения задачи;

2) веса критериев определяются в процессе решения задачи.

Способы получения экспертных оценок для первой группы методов рассмотрены в приложении.

При определении весов целевых функций экспертным путем выделяют два подхода: аксиоматический и эвристический.

При эвристическом подходе выделяют такие методы.

1. Формирование экспертных оценок.

2. Метод уступок: некоторые целевые функции заменяются ограничениями, «жесткость» которых может постепенно смягчаться.

3. Целевое программирование, в котором целевая функция имеет вид:

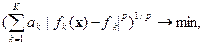
где f_k(x) – критерий; f_k – принятая цель; p – целое число.

При p = 1 говорят о линейном целевом программировании.

При использовании компьютерных расчетов, как показал анализ методов, предпочтение следует отдать второй группе методов с определением весов в процессе решения. К ним относятся метод минимальных потерь от всех критериев (метод С1) и метод идеальной точки (метод С2).

Для их формального представления введем (при G_lmin = 0) обозначение

g_l(Р) = 1 + d_l(Р),

d_l(Р) = –G_l(Р^*)/G_lmax,

где G_lmax, G_lmin ­ максимальное и минимальное значения целевых функций.

Очевидно, что g_l à min соответствует G_l à max.

В методе С1 задача векторной оптимизации приводится к виду

AP £ b,

z_l¢ ³ g_l(Р), (4.11)

z_l¢ à min.

В методе С2 первоначально определяются оптимальные значения Р^*_l и F_lmax для отдельных l-х критериев, а затем решается задача

AP £ b,

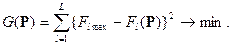
Окончательный выбор применяемого метода векторной оптимизации определяется исследователем – лицом, принимающим решения (ЛПР). Для работы ЛПР с позиций простоты алгоритма и времени его реализации можно рекомендовать метод С2, как наиболее подходящий по физическому смыслу, хотя и требующий квадратичного программирования.