Признаки оптимизационной задачи

Задачи, решаемые с помощью оптимизатора, имеют три характерных признака.

Это наличие:

- целевой ячейки;

- изменяемых ячеек;

- ограничивающих ячеек.

Целевая ячейка - единственная. В нее пользователь должен ввести формулу, указав позднее в программном диалоге, какой экстремум необходим (максимум или минимум). После завершения построения модели и инициализации расчета программа автоматически должна добиться для этой ячейки экстремального результата. Формула будет вычислять целевой показатель. Для целевой ячейки в программном диалоге (а не в самой ячейке) можно установить и конкретное целевое значение, если для его достижения необходимо будет подбирать значения взаимосвязанных с ней ячеек.

Ограничивающих ячеек может быть не менее одной на каждую изменяемую ячейку. Может существовать и некоторое количество дополнительных ячеек ограничений, например, ограничение по объему ресурса и ограничения по спросу (минимальный спрос, максимальный спрос).

Общее же количество всех ячеек, занятых под описание оптимизационной проблемы, в программе Excel не может быть более 1000.

Типы оптимизационных задач

Под признаки оптимизационной задачи подходят следующие типы задач:

- Задачи о перевозках: например, минимизация расходов по доставке товаров с нескольких фабрик в несколько магазинов с учетом спроса.

- Задачи распределения рабочих мест: например, минимизация расходов на содержание штата с соблюдением требований, определенных законодательством.

- Управление ассортиментом товаров: извлечение максимальной прибыли с помощью варьирования ассортиментным набором товаров (при соблюдении требований клиентов). Аналогичная задача возникает при продаже товаров с разной структурой затрат, рентабельностью и показателями спроса.

- Замена или смешивание материалов: например, манипуляция материалами с целью снижения себестоимости, поддержания необходимого уровня качества и соблюдения требований потребителей.

Транспортная задача

Транспортная задача является классической задачей исследования операций.

Рассмотрим простой пример транспортной задачи. Допустим, компания имеет два учебных центра и две организации. Приведем конкретные данные о загруженности каждого из учебных центров (в усл. ед.), потребности каждой организации (в усл. ед.) и стоимости обучения (тыс. руб.) (см. Таблицу 3).

Таблица 3

	Организация В1	Организация В2	Наличие образовательных чеков
Учебный центр А1
Учебный центр А2
Запрос на обучение

На пересечении столбцов и строк цифры указывают стоимость обучения в соответствующем учебном центре соответствующей организации. Графа «Наличие образовательных чеков» означает количество мест в учебном центре, а графа «Запрос на обучение» - требования (заказ) каждой организации на выделение образовательных чеков для обучения сотрудников.

Решение

Для решения задачи необходимо отвести ячейки таблицы под данные о количестве выделенных образовательных чеков учебными центрами каждой организации. Под эти данные отведены ячейки В6:С7. В ячейке D6 суммируется количество мест, выделенных организациям В1 и В2 учебным центром А1, в ячейке D7 суммируется количество мест, выделенных организациям В1 и В2 учебным центром А2.

Очевидно, что величина D6 не может превышать значение ячейки D2, т.е. в учебном центре А1 количество обучающихся не может быть больше количества имеющихся там мест. Соответственно значение ячейки D7 не может быть больше значения ячейки D3 по аналогичным соображениям, но относящимся к центру А2. В ячейках В8 и С8 суммируются количество обучающихся из организаций В1 и В2 соответственно.

Целевой ячейкой в данной задаче является ячейка В9, в которой вычисляется стоимость всех обучающихся. Последняя определяется как сумма произведений двух массивов (функция СУММПРОИЗВ): в первом на пересечении столбцов и строк находятся данные о стоимости обучения в соответствующих учебных центрах соответствующим организациям, а во втором - количество обучающихся в каждом центре из каждой организации.

Таблица 4

	А	В	С	D
		Организация В1	Организация В2	Наличие мест
	Учебный центр А1
	Учебный центр А2
	Запрос на обучение
	Учебный центр А1			=В6+С6
	Учебный центр А2			=В7+С7
		=СУММ(В6:В7)	=СУММ(С6:С7)
	Стоимость обучения	=СУММПРОИЗВ(В2:С3;В6:С7)

Рисунок 18- Образец таблицы.

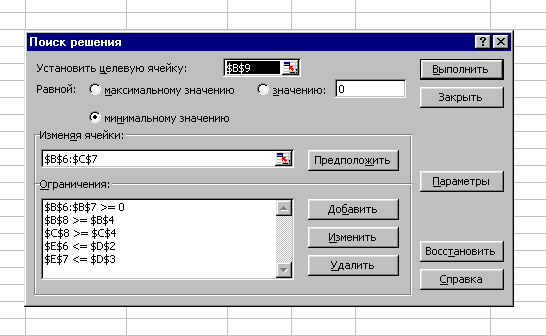В результате использования настройки Поиск решения получаем диалоговое окно (рис. 20).

Смысл ограничений состоит в следующем:

Рисунок 20–Диалоговое окно Поиск решения.

$В$6:$С$7>=0 – очевидно, что если вообще не проводить обучение, то стоимость перевозок будет минимальной. Такое «решение» задачи нас не устраивает.

$D$6<=D$2, $D$7<=D$3 – это означает, что в учебном центре количество обучающихся не может быть больше, чем там есть мест.

Рисунок 21–Результат Поиска решения.

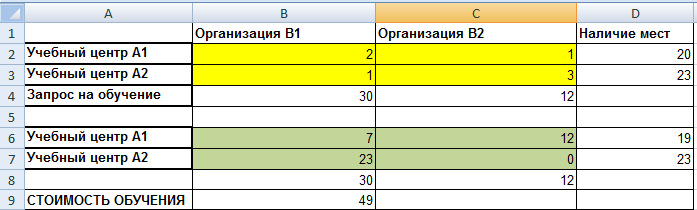$B$8>=$B$4, $C$8>=$C$4 – это означает, что запросы потребителей должны выполняться полностью. В результате запуска Поиск решений с приведенными выше ограничениями находим окончательный ответ (рис.21).

Вопросы для закрепления теоретического материала

1. Характерные признаки задач оптимизации.
2. Типы задач оптимизации.
3. Ограничения транспортной задачи.

Задание для практического занятия

Компания имеет два учебных центра (А1 и А2) и две организации (В1 и В2). Данные о загруженности каждого из учебных центров (в усл. ед.), потребности каждой организации (в усл. ед.) и стоимости обучения (тыс. руб.) приведены в таблице 5.

Таблица 5

	Организация В1	Организация В2	Наличие мест
Учебный центр А1
Учебный центр А2
Запрос на обучение

Составить план обучения сотрудников в центрах, при котором расходы организаций будут минимальными.