Алгоритм построения идеально сбалансированного дерева

Идея алгоритма: Построим и выведем на экран бинарное дерево минимальной глубины из n узлов, вычислим его глубину. Значениями узлов будут целые числа, вводимые с клавиатуры. Для получения минимальной глубины при заданном числе узлов надо располагать максимально возможное число узлов на всех уровнях, кроме самого последнего. Это достигается распределением всех поступающих узлов поровну слева и справа от каждого узла. Реализует эту идею рекурсивный алгоритм:

1. Взять один узел в качестве корня;

2. Построить левое поддерево с количеством узлов nL = n div 2 тем же способом;

3. Построить правое поддерево с количеством узлов nR = n-nL-1 тем же способом.

В программе этот алгоритм реализован рекурсивной функцией Tree.

program BinTree; {Построение идеально сбалансированного дерева,
вывод его на экран, вычисление глубины дерева}

type ref = ^Node;

Node= record

Inf: integer;

Left,Right: ref

end;

var Root: ref; {Указатель на корень дерева}

H: integer; {Высота дерева}

n: integer; {Количество узлов}

function Tree(n: integer):ref; {Рекурсивная функция построения дерева из n узлов}

var t: ref; x,nL,nR: integer;

begin

If (n=0) then Tree:=nil

else begin

nL:=n div 2; {Половина узлов – в левом поддереве}

nR:=n-nL-1; {Половина узлов минус корень – в правом поддереве}

read(x);

new(t); {Выделение динамической памяти для узла}

t^.Inf:= x; {Итак, на рекурсивном спуске }

t^.Left :=Tree(nL); {Построение левого поддерева}

t^.Right:=Tree(nR); {Построение правого поддерева}

Tree:= t

end

end; { конец функции Tree }

procedure PrintTree (t: ref; h: integer); {Вывод дерева. Обход дерева справа налево.

t – указатель на поддерево; h – уровень узла поддерева, используется для отступа от левого края экрана}

const blank=' '; {пробелы для отступа каждого уровня}

var i : integer;

begin

if (t<>nil) then begin

PrintTree (t^.Right, h+1);

for i:=1 to h do write(blank); {Отступ на уровень h}

writeln(t^.Inf);

PrintTree (t^.Left, h+1) end

end;

function Height(t:ref):integer; {Определение высоты дерева. Обход дерева снизу вверх}

var hL, hR: integer;

begin

if (t=nil) then Height:= -1 {Если дерево пустое, функция выдает значение –1}

else begin

hL:=Height(t^.Left); {Определение высоты левого поддерева}

hR:=Height(t^.Right); {Определение высоты правого поддерева}

if (hL>hR) then Height:=hL + 1

else Height:=hR + 1

end

end; { конец функции Height}

begin {основная программа}

write('n='); readln(n);

Root:= Tree(n);

PrintTree(Root, 0); {Корень дерева печатается на уровне 0, без отступа от края экрана}

H:=Height(Root); writeln('Высота H=', H)

End.

Если ввести n=7 и значения узлов 1, 2, 3, 4, 5, 6, 7, то получим на экране изображение дерева:

	7 5 6 1 4 2 3	Уровень узла: h=2 h=1 h=2 h=0 h=2 h=1 h=2
	Высота H=2

Способы обхода дерева

Обходом дерева называется последовательное обращение ко всем узлам. Существует четыре принципа упорядоченного обхода дерева, которые вытекают из его структуры. Как и саму древовидную структуру, их удобно выразить с помощью рекурсии.

Для иллюстрации обхода возьмем дерево, построенное для арифметического выражения
a*b + c/d с двухместными операциями. Замечание: для произвольного дерева обходы будут выполняться точно так же, но будут иметь другую интерпретацию.

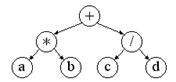В этом дереве каждая операция изображается узлом
с операндами в качестве поддеревьев.

Обозначим через Root корень дерева, а через L и R – левое и правое поддеревья.

Различные принципы обхода дают различные формы записи выражения.

1) Прямой обход, или обход сверху вниз (Root, L, R – посетить корень, затем левое и правое поддерево)
дает префиксную форму записи выражения, когда знак операции находится перед операндами:
+*ab/cd

2) Обратный обход, или обходснизу вверх (L, R, Root – посетить левое и правое поддерево, затем корень)
дает постфиксную форму записи выражения, когда знак операции находится после операндов:
ab*cd/+
Постфиксная нотация – форма записи математических выражений, в которой операнды расположены перед операторами.

3) Синтаксический обход, или обходслева направо (L, Root, R – посетить левое поддерево, затем корень и правое поддерево)
дает привычную инфиксную форму записи выражения, когда знак операции находится между операндами, к которым эта операция применяется: a*b + c/d

4) Обход справа налево (R, Root, L – посетить правое поддерево, затем корень и левое поддерево) используется для печати дерева.

Опишем обходы в виде рекурсивных процедур с параметром t, означающим ссылку на узел дерева, в частности, корень дерева. Ссылка t передается по значению, так как никаких изменений структуры дерева не происходит. Процедуры обхода вызывают некоторую процедуру OP для выполнения действий в каждом узле, например, печать узла, проверка узла на максимум и т.п.

Способы обхода дерева отличаются:

· порядком просмотра поддеревьев (левое, затем правое или правое, затем левое);

· выполнением операции над текущим узлом (на рекурсивном спуске или на рекурсивном возврате).

procedure Prefix (t: ref); {Обход сверху вниз Root, L, R} begin {дает префиксную запись выражения} if (t<>nil) then begin OP(t); {Выполняется в текущем узле на рекурсивном спуске} Prefix(t^.Left); {Переход в левое поддерево} Prefix(t^.Right) {Переход в правое поддерево} end end;	procedure Postfix(t: ref); {Обход снизу вверх L, R Root} begin {дает постфиксную запись выражения} if (t<>nil) then begin Postfix(t^.Left);{Переход в левое поддерево} Postfix(t^.Right);{Переход в правое поддерево} OP(t) {Выполняется в текущем узле на рекурсивном возврате} end end;
procedure Infix(t: ref); {Обход слева направо L, Root< R} begin {дает инфиксную, обычную запись} if (t<>nil) then begin Infix(t^.Left);{Переход в левое поддерево} OP(t); {Выполняется в текущем узле на рекурсивном возврате из левого поддерева перед рекурсивным спуском в правое поддерево} Infix(t^.Right) {Переход в правое поддерево} end end;

Деревья поиска

Двоичные деревья часто используются для представления наборов данных, элементы которого ищутся по уникальному, только им присущему ключу.

Деревом поиска называется такое бинарное дерево, в котором для ключа каждого узла все ключи его левого поддерева меньше ключа узла, а все ключи его правого поддерева больше ключа узла.

Деревья поиска можно использовать для сортировки. Например, для сортировки массива надо построить дерево поиска по значениям элементов массива, а затем обойти дерево слева направо (синтаксический обход), записывая значения узлов дерева в результирующий массив. Скорость поиска в деревьях поиска примерно такая же, что и в отсортированных массивах: O(C×log2n), в худшем случае O(n).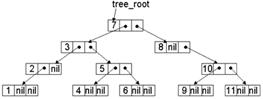

Построение дерева поиска

При построении дерева поиска и при последующем поиске узла по его ключу место каждого ключа можно найти, двигаясь, начиная от корня, и переходя на левое или правое поддерево каждого узла в зависимости от значения ключа.

Начиная с пустого дерева, очередное число ищется в дереве:

- Если число найдено, увеличивается его счетчик появления.

- Если нет, число вставляется в дерево с начальным значением счетчика=1.

Поскольку определение двоичного дерева рекурсивно, то все операции над деревом могут быть реализованы в виде рекурсивных подпрограмм. Замечание: использование рекурсии замедляет работу программы и расходует лишнюю память при её выполнении.

program TreeSearch; {Дерево поиска}

type ref=^node;

node=record

key:integer;

count:integer;

left,right:ref

end;

var Root:ref; k:integer;

procedure Gen(x:integer; var t:ref);{Генерация нового узла}

begin

new(t);

t^.key:=x; t^.count:=1;

t^.left:=nil; t^.right:=nil

end;

procedure Search (x:integer; var t:ref);{Поиск х в дереве t}

begin

if t=nil

then Gen(x,t) {Добавление узла в дерево, т.к. числа x в дереве нет}

else if (x = t^.key)

then t^.count:=t^.count+1 {Число x есть в дереве}

else if (x < t^.key)

then Search(x, t^.left) {Поиск в левом поддереве}

else Search(x, t^.right) {Поиск в правом поддереве}

end;

procedure PrintTree(t:ref; h:integer);{Вывод дерева. Обход дерева справа налево}

var i:integer;

begin

if t<>nil then

begin

PrintTree(t^.right,h+1);

for i:=1 to h do write(' ');

writeln(t^.key, ’_', t^.count);

PrintTree(t^.left, h+1);

end

end;

procedure Infix(t: ref);{Обход дерева слева направо. Дает вывод в отсортированном порядке}

begin

if (t<>nil)

then begin

Infix(t^.Left); {Переход в левое поддерево}

write(t^.key:3);

Infix(t^.Right) {Переход в правое поддерево}

end

end;

Begin

Root:=nil; {Создание пустого дерева}

write('='); readln(k);

while (k<>0) do {При k=0 построение дерева завершается}

begin

Search(k, Root);

write('='); readln(k);

end;

PrintTree(Root,0);{Вывод дерева}

Infix(Root); {Вывод листьев дерева в отсортированном порядке}

End.