Модели оценки надежности программ

Оценка и прогнозирование надежности программ осуществляется на основе математических моделей надежности программ. Общие предпосылки для всех моделей следующие. В начальный момент времени программа работает и сохраняет свою работоспособность до окончания интервала времени t1, когда обнаруживается ошибка в программе. Программист исправляет программу, которая затем исправно работает до t2 и т.д. Т.о. для построения вероятностной модели имеется:

А) Случайное время между двумя последовательными отказами, к-е имеет функцию плотности распределения f(t/l_i) появления ошибок

Б) число оставшихся ошибок в программе

Самой известной моделью надежности является модель Джелински-Моранды, опирающая на модели надежности аппаратуры.

Пусть R(t) - функция надежности, т.е. вероятность того, что ни одна ошибка не появится в интервале от 0 до t. F(t)=1-R(t) - функция отказов. Соответственно плотность вероятности f(t)=-dR(t)/dt.

Вводится функция риска z(t)-условная вероятность тог, что ошибка появится на интервале от t до t+Dt, при условии, что до момента t ошибок не было. По аналогии z(t)=f(t)/R(t) и

,

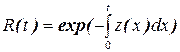а среднее время между отказами интеграл от 0 до ¥ от функции R(t).

Основной такой модели является уточнение поведения функции z(t). При оценке надежности аппаратуры аналогичный параметр - интенсивность =константе. Однако предположение о постоянстве функции риска представляется не соответствующим реальности в случае программного обеспечения, так как по мере обнаружения и исправления ошибок, время между сбоями увеличивается.

В Модели делается существенное предположение о том, что z(t) постоянна от исправления одной ошибки до обнаружения следующей, после чего z(t) опять становится константой, но уже с другим, меньшим значением. То есть z(t) пропорциональна числу оставшихся ошибок.

Второе предположение z(t) - прямо пропорциональна числу оставшихся ошибок, z(t)=K(N-i), где N - неизвестное первоначальное число ошибок, i - число обнаруженных ошибок, K - некоторая неизвестная константа. Каждый раз, когда ошибка обнаруживается (модель предполагает, что задержка между обнаружением ошибки и ее исправлением отсутствует) z(t) уменьшается на некоторую величину К.

Дальнейшая проработка этой модели -Модель Шумана относится к динамическим моделям дискретного времени, данные для которой собираются в процессе тестирования программного обеспечения в течение фиксированных или случайных интервалов времени

Предполагается, что в начальный момент компоновки программных средств в систему программного обеспечения в них имеется Е_т шибок. С этого времени начинается отсчет времени отладки t, которое включает затраты времени на выявление ошибок с помощью тестов.

Модель Шумана предполагает, что тестирование проводится в несколько этапов. Каждый этап представляет собой выполнение программы на полном комплексе разработанных тестовых данных. Выявленные ошибки регистрируются, но не исправляются. В конце этапа рассчитываются количественные показатели надежности, исправляются найденные ошибки, корректируются тестовые наборы и проводится следующий этап тестирования. В модели Шумана предполагается, что число ошибок в программе постоянно и в процессе корректировки новые ошибки не вносятся.

На основании полученных для каждого этапа времен и кол-ва ошибок рассчитываются параметры функции риска.

У этой модели много недостатков. Прежде всего, предположения об ошибках, не все ошибки программ достаточно серьезны (ошибка в тексте и результате). Далее - ошибка немедленно исправляется и по мере исправления одной ошибки в программу не вносятся другие. Поэтому дальнейшая модификация этой модели развивалась в направлении поиска и определения других функций риска.(схема 2). Есть работы показывающие, что для одной программы функция риска меняется со временем или при обнаружении каждой ошибки.

Существует модель Миллса, в которой не делается никаких предположений о поведении функции риска, а модель строится на статистике. Ошибки специально вносятся в программу случайным образом. Путем тестирования программы в течении некоторого времени и отсортировывая собственные и внесенные ошибки, можно оценить первоначальное число ошибок в программе.

Предположим, что в программу внесено s ошибок, после чего начато тестирование. При тестировании обнаружено n - число собственных ошибок, v - число найденных внесенных. Тогда N=sn/v.

Далее решается задача проверки гипотезы об N. (насколько полученное значение соответствует реальному по данному кол-ву внесенных ошибок). Тестирование проводится до обнаружения всех внесенных ошибок. Уровень значимости (мера доверия к модели) определяется: С=s/(s+k+1), k - кол-во обнаруженных собственных ошибок.