Пример расчета значений напряжения течения металла с использованием компьютерной программы
В качестве примера рассмотрим определение значения 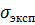 при заданных значениях факторов
при заданных значениях факторов 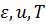 для стали 08кп [3]. При этом в Каталоге открывается группа «Конструкционные стали», а затем подгруппа «Нелегированные конструкционные качественные стали» и в соответствующую папку заносится отсканированная графическая информация, включающая кривые упрочнения и подрисуночную надпись.
для стали 08кп [3]. При этом в Каталоге открывается группа «Конструкционные стали», а затем подгруппа «Нелегированные конструкционные качественные стали» и в соответствующую папку заносится отсканированная графическая информация, включающая кривые упрочнения и подрисуночную надпись.
На рис.4.14, в таблицах, расположенных в правой части окна, задаются имеющееся на графиках количество значений 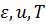 , их величина и маркировка. Задается также химический состав стали, если он указан.
, их величина и маркировка. Задается также химический состав стали, если он указан.
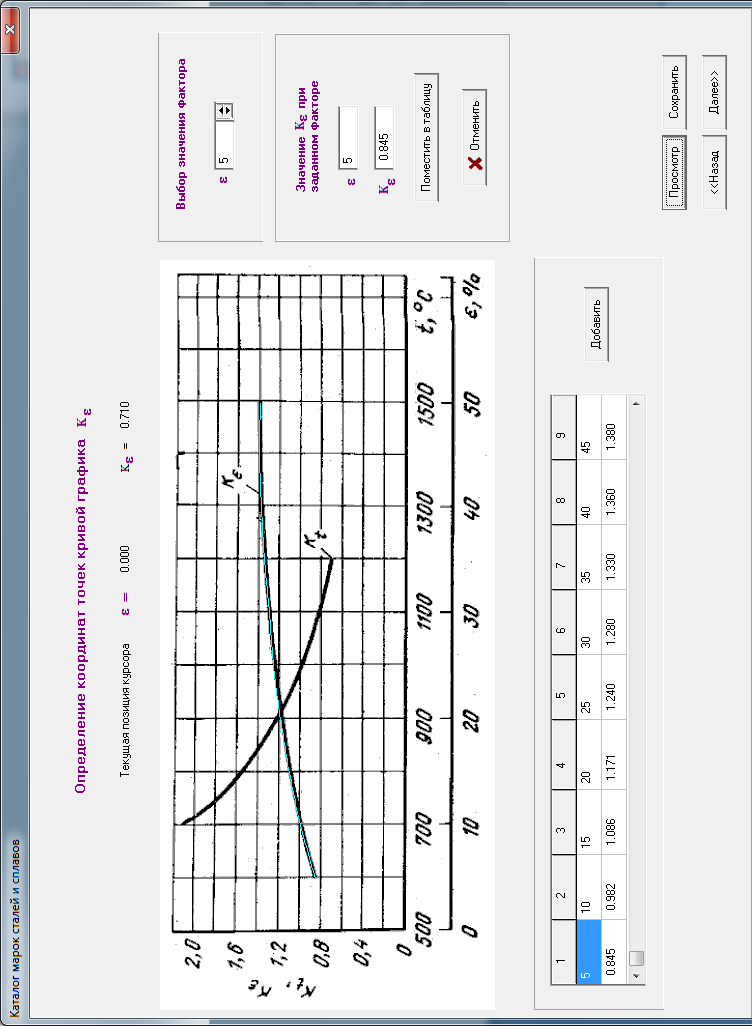
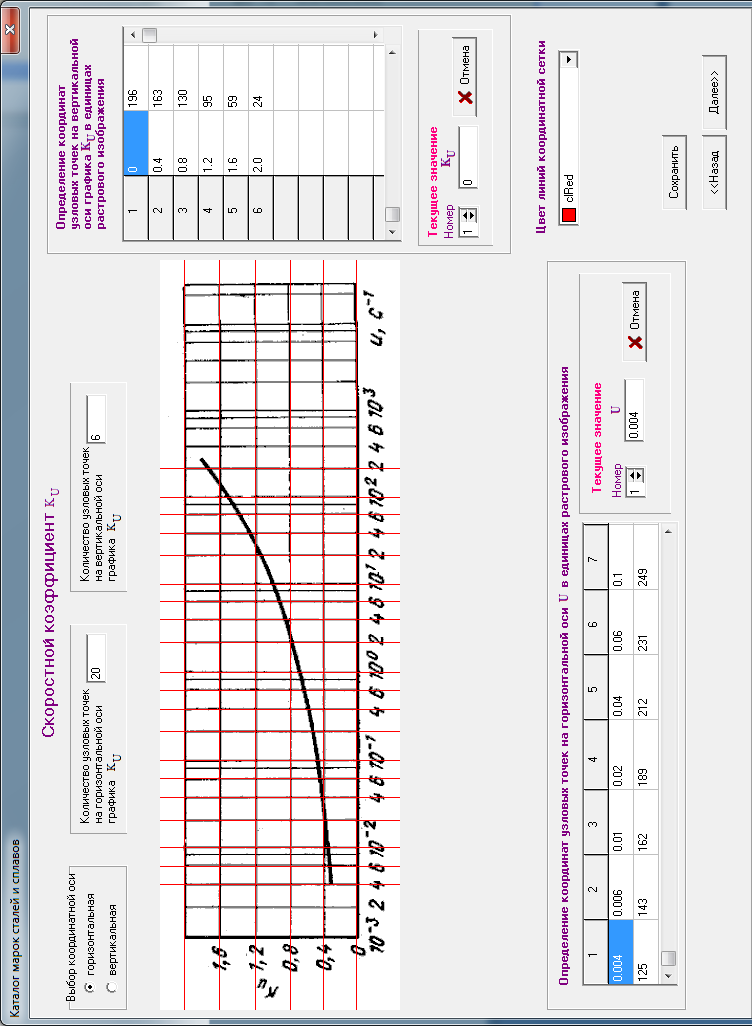
В окне (см. рис. 4.15) поочередно для всех узловых точек координатных осей ставятся в соответствие значения 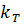 и
и 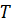 в единицах, указанных на координатных осях, а также в единицах растрового изображения, которые определяются программно. В таблицу автоматически заносится значение абсциссы узловой точки в единицах растрового изображения, а на самом рисунке вычерчивается вертикальная линия. Аналогичные действия выполняются и для оси ординат.
в единицах, указанных на координатных осях, а также в единицах растрового изображения, которые определяются программно. В таблицу автоматически заносится значение абсциссы узловой точки в единицах растрового изображения, а на самом рисунке вычерчивается вертикальная линия. Аналогичные действия выполняются и для оси ординат.
На основе полученной информации для любой точки, лежащей на графике, можно определить абсциссу и ординату в растровых единицах, а затем рассчитать их в единицах, указанных на координатных осях. В правой части окна (рис.4.16) имеется переключатель выбора текущих значений 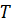 . Программа вычисляет значение
. Программа вычисляет значение 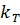 , а после нажатия кнопки "Поместить в таблицу" заносит его в таблицу.
, а после нажатия кнопки "Поместить в таблицу" заносит его в таблицу.
Далее выполняется сплайн-интерполяция полученной информации и построение сплайн - кривой в окне рис.4.16.
Аналогичные действия выполняются для графиков кривых 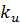 ,
, 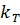 . Окна программы представлены на рис. 4.17-4.20.
. Окна программы представлены на рис. 4.17-4.20.
На основе полученной информации выполняется расчет величин 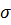 (см. рис.4.21) и передается в таблицу окна (см. рис.4.22). Таблица представленная на рис.4.22, используется для определения значения напряжения течения металла при заданных значения факторов
(см. рис.4.21) и передается в таблицу окна (см. рис.4.22). Таблица представленная на рис.4.22, используется для определения значения напряжения течения металла при заданных значения факторов 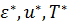 . В правой части окна, в соответствующие поля вводятся значения
. В правой части окна, в соответствующие поля вводятся значения 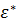 ,
, 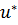 и
и 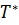 при которых требуется определить значение напряжения течения металла
при которых требуется определить значение напряжения течения металла 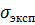 .
.
Для этого в соответствующие поля (см.рис. 4.22) вводим значения: 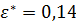 ,
, 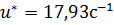 ,
, 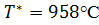 и получаем значение напряжения течения металла, равное
и получаем значение напряжения течения металла, равное 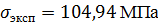 .
.
Расчет 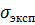 при других значениях
при других значениях 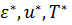 выполняется аналогично в окне программы см. рис.4.22.
выполняется аналогично в окне программы см. рис.4.22.
 | Рисунок 4.14 - Окно исходной информации |
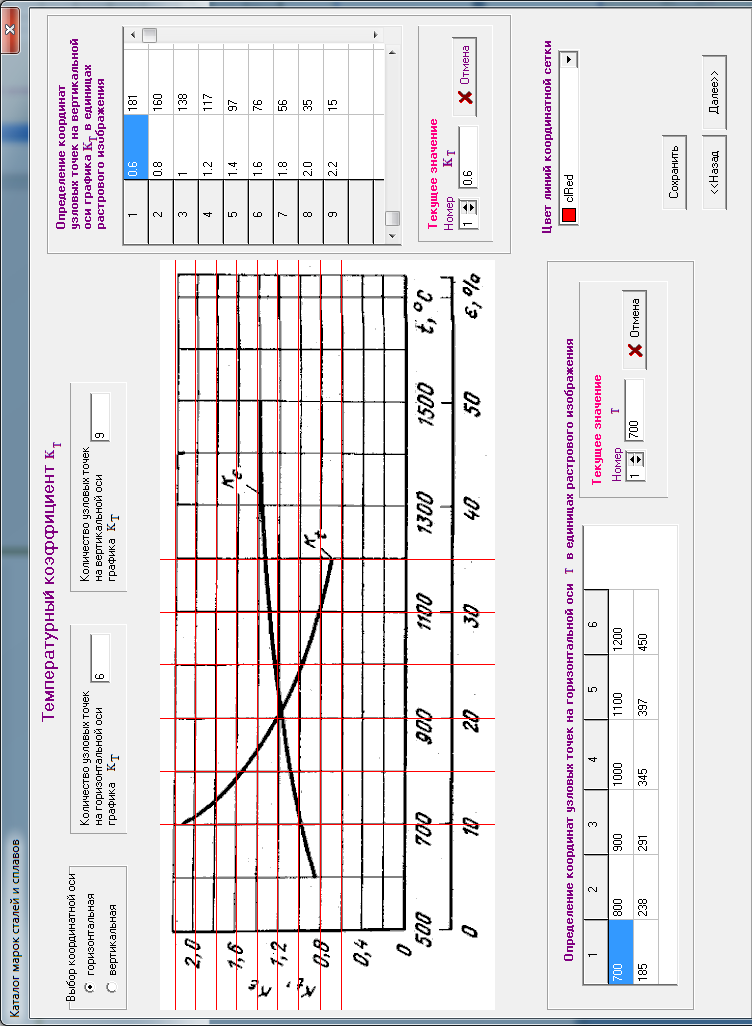 | Рисунок 4.15 - Окно построения координатной сетки  |
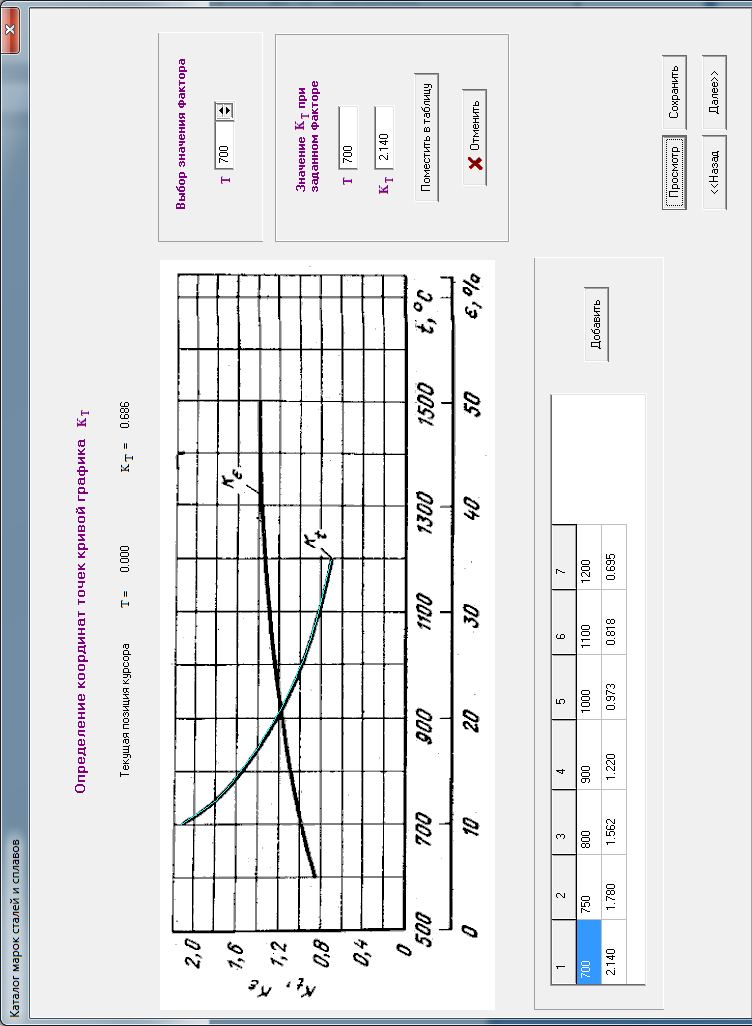 | Рисунок 4.16 - Окно снятия экспериментальной информации 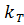 и контрольного построения сплайн – кривой и контрольного построения сплайн – кривой |
 | Рисунок 4.17 - Окно построения координатной сетки  |
 | Рисунок 4.18 - Окно снятия экспериментальной информации  и контрольного построения сплайн – кривой и контрольного построения сплайн – кривой |
 | Рисунок 4.19 - Окно построения координатной сетки  |
 | Рисунок 4.20 - Окно снятия экспериментальной информации 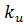 и контрольного построения сплайн – кривой и контрольного построения сплайн – кривой |
 | Рисунок 4.21 - Окно экспериментальных значений напряжения течения металла в зависимости от факторов 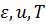 |
 | Рисунок 4.22- Окно расчета напряжения течения на основе экспериментальной информации при требуемых значениях 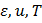 |
Пример разработки эмпирической формулы на базе теории планируемого эксперимента
4.2.1 Планирование расчетного эксперимента в зависимости от трех факторов 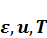
Эксперимент спланирован в зависимости от трех факторов 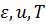 , что позволяет учесть в различных опытах наиболее рациональные варианты их сочетаний. Важным этапом является построение план - матрицы проведения эксперимента и разработка формулы для расчета напряжения течения металла при горячей пластической деформации.
, что позволяет учесть в различных опытах наиболее рациональные варианты их сочетаний. Важным этапом является построение план - матрицы проведения эксперимента и разработка формулы для расчета напряжения течения металла при горячей пластической деформации.
Исходя из представленной в технической литературе экспериментальной информации для стали 15СХНД [1] определим следующие диапазоны изменения факторов 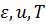 :
:
0,05 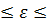 0,50;
0,50;
0,05, с-1 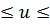 50, с-1; (4.1)
50, с-1; (4.1)
900, ºС 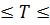 1200, ºС.
1200, ºС.
Указанные диапазоны изменения факторов могут быть уменьшены в зависимости от поставленной задачи.
Эксперимент спланирован по плану второго порядка. Применено центральное композиционное ортогональное планирование для n=3 (n – число факторов). Связь между натуральными и кодовыми переменными определяется по формуле 3.2.
Выполним расчет значения фактора ε на нулевом уровне:

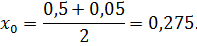
Определим интервал варьирования фактора 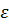 . Запишем формулу (3.3):
. Запишем формулу (3.3):

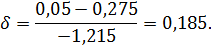
Выполним расчет натуральных значений фактора 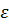 на основе кодовых:
на основе кодовых:

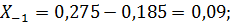

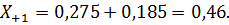
Аналогичным образом выполняется расчет уровней варьирования для факторов 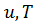 . Результаты кодирования факторов и установленные уровни их варьирования представлены в табл. 4.3.
. Результаты кодирования факторов и установленные уровни их варьирования представлены в табл. 4.3.
Таблица 4.3 – Кодирование факторов и уровни их варьирования
| Интервал варьирования и уровни факторов | 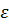 | 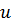 , с-1 , с-1 | 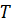 ,ºС ,ºС |
Нулевой уровень, 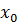 | 0,275 | 25,25 | |
Интервал варьирования, 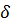 | 0,185 | 20,37 | 123,5 |
Нижний уровень, 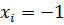 | 0,09 | 4,88 | 926,5 |
Верхний уровень, 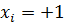 | 0,46 | 45,62 | 1173,5 |
Нижний уровень в звездной точке, 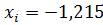 | 0,05 | 0,5 | |
Верхний уровень в звездной точке, 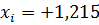 | 0,5 |
На основе значений факторов на разных уровнях их варьирования разработана расчетная план матрица проведения эксперимента (табл.4.4).
Для разработки искомой формулы применительно к любой марке стали необходимо реализовать 15 опытов при различных температурно-скоростных и деформационных условиях.
После этого требуется определить экспериментальные значения напряжения течения металла 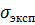 , при заданных значения факторов
, при заданных значения факторов 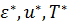 для каждого из 15 опытов.
для каждого из 15 опытов.
Последовательность определения значения напряжения течения металла дана в п. 3.1, а пример расчета - в пункте 4.1. Результаты расчета 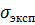 представленны в табл.4.5.
представленны в табл.4.5.
Таблица 4.4 – План-матрица эксперимента
| Блоки плана | Номер опыта | Факторы, их кодовые и натуральные значения | |||||
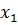 | 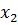 | 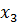 | 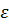 | 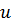 , с-1 , с-1 | 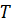 ,ºС ,ºС | ||
| Ядро плана | -1 | -1 | -1 | 0,090 | 4,88 | 926,5 | |
| -1 | -1 | 0,460 | 4,88 | 926,5 | |||
| -1 | -1 | 0,090 | 45,62 | 926,5 | |||
| -1 | 0,460 | 45,62 | 926,5 | ||||
| -1 | -1 | 0,090 | 4,88 | 1173,5 | |||
| -1 | 0,460 | 4,88 | 1173,5 | ||||
| -1 | 0,090 | 45,62 | 1173,5 | ||||
| 0,460 | 45,62 | 1173,5 | |||||
| «Звездные» точки | -1,215 | 0,050 | 25,25 | 1050,0 | |||
| 1,215 | 0,500 | 25,25 | 1050,0 | ||||
| -1,215 | 0,275 | 0,50 | 1050,0 | ||||
| 1,215 | 0,275 | 50,00 | 1050,0 | ||||
| -1,215 | 0,275 | 25,25 | 900,0 | ||||
| 1,215 | 0,275 | 25,25 | 1200,0 | ||||
| Нулевая точка | 0,275 | 25,25 | 1050,0 |
Таблица 4.5 – Результаты расчета 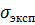 в запланированных опытах
в запланированных опытах
