Найпростіші потоки з можливою неординарністю
Найпростіший потік з можливою неординарністю має властивості стаціонарності і відсутності післядії. Вимоги в такому потоці можуть надходити не по одному, а відразу групами (пакетами). У цьому випадку усі вимоги, що приходять одночасно, поєднуються в пакети, ймовірність надходження двох чи більше пакетів за проміжок часу t є величина, нескінченно мала стосовно t. Кожен пакет, виходячи з визначення, містить хоча б одну вимогу.
Ймовірність надходження k вимог для потоку з можливою неординарністю з урахуванням ймовірності pm перебування m вимог у пакеті
 , при
, при 
Найпростіші потоки з можливою післядією
Потік, що має кінцеве значення параметра і має властивості стаціонарності, й ординарності є найпростішим потоком з можливою післядією. Умовна ймовірність надходження деякої кількості вимог на заданий проміжок часу t такого потоку обчислюється за допомогою припущення про передісторію потоку (про надходження вимог до цього проміжку часу) і може відрізнятися від безумовної ймовірності тієї ж події.
Ймовірність надходження вимог k за даний проміжок часу t для потоку з можливою післядією має такий вигляд
 ,
,
де  – функція Пальма-Хінчина.
– функція Пальма-Хінчина.
Функція  є ймовірністю надходження k вимог за час t за умови, що в початковий момент цього проміжку t надійде хоча б одна (а в силу ординарності потоку рівно одна) вимога (ця початкова вимога не входить у кількість k вимог за час t).
є ймовірністю надходження k вимог за час t за умови, що в початковий момент цього проміжку t надійде хоча б одна (а в силу ординарності потоку рівно одна) вимога (ця початкова вимога не входить у кількість k вимог за час t).
Потоки Пальма
Ординарний потік подій називається потоком Пальма (або рекурентним потоком, чи потоком з обмеженою післядією), якщо інтервали часу  між послідовними подіями є незалежними, однаково розподіленими випадковими величинами.
між послідовними подіями є незалежними, однаково розподіленими випадковими величинами.
У зв'язку з рівністю розподілів  потік Пальма завжди стаціонарний. Найпростіший потік є частковим випадком потоку Пальма; у ньому інтервали між подіями розподілені за показовим законом.
потік Пальма завжди стаціонарний. Найпростіший потік є частковим випадком потоку Пальма; у ньому інтервали між подіями розподілені за показовим законом.
Потоки Ерланга
Потоком Ерланга n-го порядку називається потік подій, що виходить «проріджуванням» найпростішого потоку, коли зберігається кожна n-а точка (подія) у потоці, а всі проміжні відкидаються.
Інтервал часу між двома сусідніми подіями в потоці Ерланга n-го порядку є сумою n незалежних випадкових величин  , що мають показовий розподіл з параметром
, що мають показовий розподіл з параметром 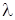 :
:
 .
.
Закон розподілу випадкової величини Т називається законом Ерланга n-го порядку і має щільність
 (при t>0).
(при t>0).
Математичне очікування, дисперсія і середнє квадратичне відхилення випадкової величини Т відповідно рівні:
 ;
;  ;
;  .
.
Для потоків Ерланга n-го порядку ймовірність надходження k вимог за проміжок часу t дорівнює
 , для k>0.
, для k>0.
При k=0
 .
.
