Формирование математической модели. F0 = 0 – нулевое значение ряда Фибоначчи;
Исходные данные
f0 = 0 – нулевое значение ряда Фибоначчи;
f1 = 1 – первое значение ряда Фибоначчи;
fгр = 100 – граничное значение.
Расчётные зависимости
fi = fi-2 + fi-1 – формирование текущего значения ряда;
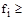fгр – условие прекращения вычислений.
Выбор метода решения
Анализ математической модели задачи показывает, что решение требует многократного расчёта новых значений чисел fi. Расчет выполняется до тех пор, пока текущее fi не превышает граничное значение fгр (fгр = 100). Расчётная зависимость формирования следующего значения fi+1 через предыдущие fi, определяет выбор рекуррентного метода. Особенность задачи предписывает расчёт текущего значения через два предыдущих:
fi = fi-2 + fi-1.
Следовательно, параметр цикла (fi) имеет два начальных значения
fi-2 = 0, fi-1 = 1.
Закон изменения определяют зависимости:
fi-2 = fi-1 и fi-1 = fi.
Граничное значение (fгр = 100) определяет условие повторения процесса счёта fi < fгр, (обратное заданному для прекращения вычислений в постановке задачи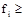 
fгр).
Следовательно, в качестве метода решения требуется циклический вычислительный процесс с неизвестным числом повторений, выполняемый до получения результата с заданной границей (итерационный цикл с точным решением).
Составление алгоритма решения
Представим алгоритм решения задачи двумя одношаговыми схемами (рис. 7.7). Схема (а) предусматривает хранение всех получаемых значений чисел Фибоначчи в виде одномерного массива, в схеме (б) – хранение значений не предусмотрено.
Программирование задачи
Каждый вариант расчета оформим в виде отдельной функции. Для варианта (а) алгоритма идентификация переменных представлена в табл. 7.2, для варианта (б) – в табл. 7.3.
Таблица 7.2
| Обозначение в алгоритме | i | fгр | f0 | fi | fi-2 | fi-1 |
| Обозначение в программе | i | fgr | f[0] | f[ i ] | f[i-2] | f[i-1] |
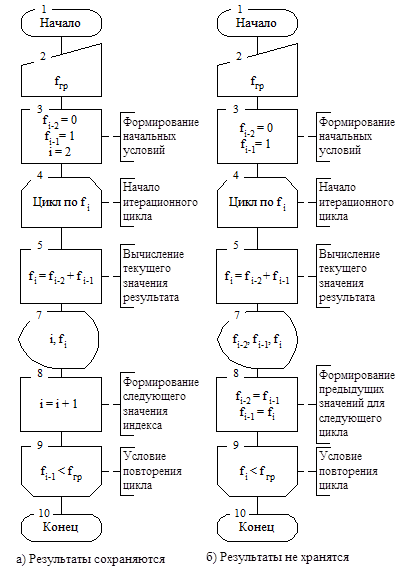
Рис. 7.7 Схемы алгоритмов решения задачи Фибоначчи
Таблица 7.3
| Обозначение в алгоритме | i | fгр | f0 | fi | fi-2 | fi-1 |
| Обозначение в программе | i | fgr | f0 | fi | fi2 | fi1 |
Программы решения задачи по схемам алгоритма с учетом таблицы идентификации переменных представлены ниже.
Классический вариант программирования задачи
Программа решения по варианту (а)
#include <stdlib.h> /* директивы */
#include <stdio.h> /* препроцессора */
#include <conio.h>
#include <windows.h>
main( ) /* заголовок головной функции */
{
int i, fgr, f[100]; /* описатели переменных и массива */
char buf[50]; /* описатель символьного массива */
CharToOem("\n Введите граничное значение ряда : ",buf);
printf(buf);
scanf("%d", &fgr);
i = 2; /* задание начального значения индекса */
f[0] = 0; /* формирование значения первого члена ряда */
f[1] = 1; /* формирование значения второго члена ряда */
printf("\n ----------------"
"\n | i | fi |"
"\n ----------------");
do
{
f[ i ] = f[ i - 2 ] + f[ i - 1 ]; /* расчет i–го члена ряда */
printf("\n | %3d | %3d |", i - 1, f[ i ]);
i = i +1; /* формирование нового значения номера итерации */
}while( f[ i - 1 ] < fgr ); /*условие выхода их цикла */
printf("\n ----------------\n");
getch();
}
Под закрывающей скобкой программы приведено исходное данное для решения задачи.
Программа решения по варианту (б)
#include <stdlib.h> /* директивы */
#include <stdio.h> /* препроцессора */
#include <conio.h>
#include <windows.h>
main( ) /* заголовок головной функции */
{
int fgr, fi, fi1, fi2; /* описатели переменных и массива */
char buf[50]; /* описатель символьного массива */
CharToOem("\n Введите граничное значение ряда : ",buf);
printf(buf);
scanf("%d", &fgr);
fi2 = 0; /* формирование значения первого члена ряда */
fi1 = 1; /* формирование значения второго члена ряда */
printf("\n ------------------------------"
"\n | f(i-2) | f(i-1) | f(i) |"
"\n ------------------------------");
do
{
fi = fi2 + fi1; /* расчет i–го члена ряда */
printf( "\n | %3d | %3d | %3d |", fi2, fi1, fi);
fi2 = fi1; /* формирование новых значений */
fi1 = fi; /* параметров через предыдущие */
}while( fi < fgr ); /*условие выхода их цикла */
printf("\n ------------------------------");
getch();
}
100 – исходное данное для решения задачи.
Результаты решения представлены в приложении 7.3 (варианты а, б).
Программирование задачи с графическим интерфейсом
Программирование задачи при использовании графического интерфейса предварим его разработкой. Для ввода граничного значения ряда планируем поле редактирования (EditFgr). Под вывод расчетных значений используем поле-список (ListBoxFi).
|
|
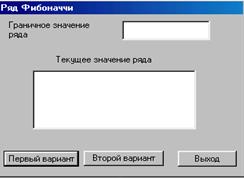
Управление процессом решения (в двух планируемых вариантах) реализуем тремя командными кнопками, расположенными в нижней части окна. Назначение каждой определяется ее названием.
С учетом планируемого интерфейса выполним последовательное программирование задачи по каждой схеме. Варианты расчета оформим в виде отдельных функций.
Программа решения по варианту (а)
#include <stdlib.h> /* директивы */
#include <stdio.h> /* препроцессора */
…
void TIter2DlgClient::BNClickedOK() /* заголовок функции */
{
// INSERT>> Your code here.
int i, fgr, f[100]; /* описатели переменных и массива */
char buf[25]; /* описатель символьного массива */
ListBoxFi->ClearList(); /* очистка поля-списка */
EditFgr->GetText(buf,10); /* ввод граничного */
fgr=atoi(buf); /*значения ряда */
i = 2; /* задание начального значения индекса */
f[0] = 0; /* формирование значения первого члена ряда */
f[1] = 1; /* формирование значения второго члена ряда */
do
{
f[i] = f[i-2] + f[i-1]; /* расчет i–го члена ряда */
sprintf(buf,"%3d %5d",i ,f[i]); /* вывод номера итерации */
ListBoxFi->AddString(buf); /* и текущего значения fi*/
i = i +1; /* формирование нового значения номера итерации */
}while( f[i-1] < fgr ); /*условие выхода их цикла */
}
100 – исходное данное
Программа решения по варианту (б)
#include <stdlib.h> /* директивы */
#include <stdio.h> /* препроцессора */
…
void TIter2DlgClient::BNClickedOK2() /* заголовок функции */
{
// INSERT>> Your code here.
int fgr, fi, fi1, fi2; /* описатели переменных */
char buf[25]; /* описатель символьного массива */
ListBoxFi->ClearList(); /* очистка поля-списка */
EditFgr->GetText(buf,10); /* ввод граничного */
fgr=atoi(buf); /*значения ряда */
fi2 = 0; /* формирование значения первого члена ряда */
fi1 = 1; /* формирование значения второго члена ряда */
do
{
fi = fi2 + fi1; /* расчет текущего члена ряда */
sprintf(buf,"%5d %5d %5d ",fi2, fi1, fi);/* вывод текущих */
ListBoxFi->AddString(buf); /* значения fi2, fi1, fi */
fi2 = fi1; /* формирование новых значений */
fi1 = fi; /* параметров через предыдущие */
}while( fi < fgr ); /*условие выхода их цикла */
}
100 – исходное данное
Результаты решения представлены в приложении 7.4 (варианты а, б).