Представлення графів матрицею суміжності

Для цього подання будується матриця 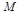розміром 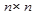, де 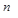- кількість вузлів графа. У елементі 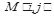знаходиться вага ребра. В інших елементах знаходяться нулі.

Представлення графів списками суміжності.

Для цього подання створюється масив, розмірністю, що дорівнює кількості вузлів графа. Цей масив містить покажчики на списки, що містять суміжні вузли для даної вершини.

Алгоритм Дейкстри для знаходження найкоротшого шляху між вершинами орграфа.

Алгоритм будує множену вершин 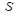, для яких найкоротші шляхи від джерела вже відомі. На кожному кроці до множени 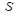додається та з решти вершин, відстань до якої від джерела менше, ніж для інших, що залишилися вершин. Якщо вартості всіх дуг позитивні, то можна бути впевненим, що найкоротший шлях від джерела до конкретної вершини проходить тільки через вершини множини 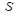. Назвемо такий шлях особливим. На кожному кроці алгоритму використовується також масив 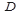, в який записуються довжини найкоротших особливих шляхів для кожної вершини. Коли множена 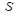буде містити всі вершини орграфа, тобто для всіх вершин будуть знайдені "особливі" шляхи, тоді масив 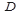буде містити довжини найкоротших шляхів від джерела до кожної вершини.

Приклад.

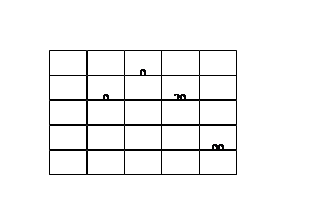
Розглянемо роботу алгоритму на прикладі графа, показаного на малюнку. Нехай потрібно знайти відстані від 1-ї вершини до всіх інших.

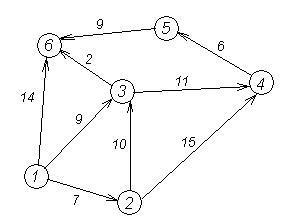
У вершинах позначені їх номери, над ребрами позначена їх «ціна» - довжина шляху. Поряд з кожною вершиною червоним позначена мітка - довжина найкоротшого шляху в цю вершину з вершини 1.

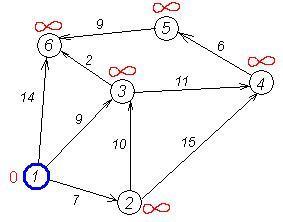
Перший крок. Розглянемо крок алгоритму Дейкстри для нашого прикладу. Мінімальну мітку має вершина 1. Її сусідами є вершини 2, 3 та 6.

Перший по черзі сусід вершини 1 - вершина 2, тому що довжина шляху до неї мінімальна. Довжина шляху в неї через вершину 1 дорівнює найкоротшій відстані до вершини 1 + довжина ребра, що йде з 1 в 2, тобто 0 + 7 = 7. Це менше поточної мітки вершини 2, тому нова мітка 2-й вершини дорівнює 7.

Аналогічну операцію проробляємо з двома іншими сусідами 1-й вершини - 3-й і 6-й.

Всі сусіди вершини 1 перевірені. Поточне мінімальна відстань до вершини 1 вважається остаточним і перегляду не підлягає (те, що це дійсно так, вперше довів Дейкстра). Викреслимо її з графа, щоб відзначити, що ця вершина відвідана.

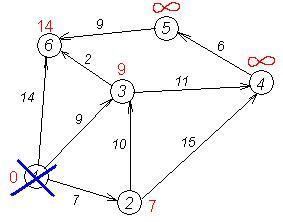
Другий крок. Крок алгоритму повторюється. Знову знаходимо «найближчу» з невідвіданих вершин. Це вершина 2 з міткою 7.

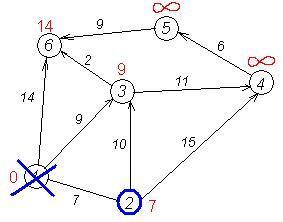
Знову намагаємося зменшити мітки сусідів обраної вершини, намагаючись пройти в них через 2-гу вершину. Сусідами вершини 2 є 1, 3, 4.

Перший (по порядку) сусід вершини 2 - вершина 1. Але вона вже відвідали, тому з 1-й вершиною нічого не робимо.

Наступний сусід вершини 2 - вершини 4 і 3. Якщо йти в 4 через 2-гу, то довжина такого шляху буде = найкоротша відстань до 2-ї + відстань між вершинами 2 і 4 = 7 + 15 = 22. Оскільки 22 <∞, встановлюємо, що мітка вершини 4 дорівнює 22.

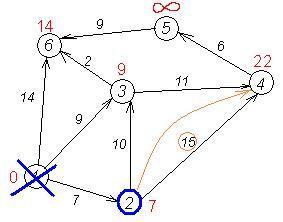
Ще один сусід вершини 2 - вершина 3. Якщо йти в неї через 2-гу, то довжина такого шляху буде = 7 + 10 = 17. Але поточна мітка третьої вершини дорівнює 9 <17, тому мітка не змінюється.

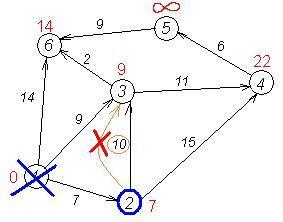
Всі сусіди вершини 2 проглянуті, заморожуємо відстань до неї і позначаємо її як відвідану.

Третій крок. Повторюємо крок алгоритму, вибравши вершину 3.

Подальші кроки. Повторюємо крок алгоритму для решти вершин (Це будуть по порядку 6, 4 та 5).

Завершення виконання алгоритму. Алгоритм закінчує роботу, коли викреслені всі вершини. Результат його роботи: найкоротший шлях від вершини 1 до 2 складає 7, до 3 = 9, до 4 = 20, до 5 = 20, до 6 = 11.

Оскільки алгоритм Дейкстри щоразу вибирає для обробки вершини з найменшою оцінкою найкоротшого шляху, можна сказати, що він відноситься до жадібних алгоритмів.