Краткие теоретические сведения и методические указания к выполнению работы.

Метрики цикломатической сложности по Маккейбу

Вторая наиболее представительная группа оценок сложности программ – метрики сложности потока управления программ. Как правило, с помощью этих оценок оперируют либо плотностью управляющих переходов внутри программ, либо взаимосвязями этих переходов.

Метрики второй группы базируются на анализе управляющего графа программы. Представителем данной группы является метрика Маккейба.

Управляющий граф программы, который используют метрики данной группы, может быть построен на основе алгоритмов модулей. Поэтому метрики второй группы могут применяться для оценки сложности промежуточных продуктов разработки.

Стало традиционным представление программ в виде управляющего ориентированного графа G=(V,E), где V – вершины, соответствующие операторам, Е – дуги, соответствующие переходам. В дуге (u,v)вершина v является исходной, а u – конечной. При этом u непосредственно следует за v, а v непосредственно предшествует u. Если путь от v до u состоит более чем из одной дуги, тогда u следует за v, а v предшествует u.

Впервые графическое представление программ было предложено Маккейбом. Основной метрикой сложности он предлагает считать цикломатическую сложность графа программы или, как её ещё называют, цикломатическое число Маккейба, характеризующее трудоёмкость тестирования программы. Показатель цикломатической сложности позволяет не только произвести оценку трудоемкости реализации отдельных элементов программного проекта и скорректировать общие показатели оценки длительности и стоимости проекта, но и оценить связанные риски и принять необходимые управленческие решения.

Для вычисления цикломатического числа Маккейба z(G) применяется формула

z(G)=e-v+2p, (7)

где е – число дуг ориентированного графа Q; v – число вершин; р – число компонентов связности графа.

Число компонентов связности графа можно рассматривать как количество дуг, которые необходимо добавить для преобразования графа в сильносвязный. Сильносвязным называется граф, любые две вершины взаимно достижимы. Для графов корректных программ, то есть графов, не имеющих недостижимых от точки входа участков и "висячих" точек входа и выхода, сильносвязный граф, как правило, получается путём замыкания дугой вершины, обозначающей конец программы на вершину, обозначающую точку входа в эту программу.

В процессе автоматизированного вычисления показателя цикломатической сложности, как правило, применяется упрощенный подход, в соответствии с которым построение графа не осуществляется, а вычисление показателя производится на основании подсчета числа операторов управляющей логики (if, switch и т.д.) и возможного количества путей исполнения программы.

Показатель цикломатической сложности может быть рассчитан для модуля, метода и других структурных единиц программы.

Существует значительное количество модификаций показателя цикломатической сложности.

· "Модифицированная" цикломатическая сложность – рассматривает не каждое ветвление оператора множественного выбора (switch), а весь оператор как единое целое.

· "Строгая" цикломатическая сложность – включает логические операторы.

· "Упрощенное" вычисление цикломатической сложности – предусматривает вычисление не на основе графа, а на основе подсчета управляющих операторов.

По сути z(G) определяет число линейно независимых контуров в сильно связном графе. Иначе говоря, цикломатическое число Маккейба показывает требуемое количество проходов для покрытия всех контуров сильносвязного графа или количество текстовых прогонов программы, необходимых для исчерпывающего тестирования по критерию "работает каждая ветвь".

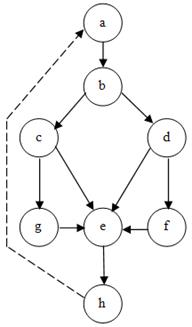
Рис.1. Граф управления программы

Для программ, граф которой изображён на рис.1, цикломатическое число при е=10, v=8, p=1 определяется как z(G)=10-8+2=4. Таким образом, имеется сильно связный граф с четырьмя линейно независимыми контурами:

a-b-c-g-e-h-a;

a-b-c-e-h-a;

a-b-d-f-e-h-a;

a-b-d-e-h-a;

По определению управляющего графа программы, вершины (a-b) и (e-h) следовало бы объединить, но, по сути, это ничего не меняет, т.к. z остаётся без изменений:

z(G)=8-6+2=4.

Цикломатическое число зависит только от количества предикатов, сложность которых при этом не учитывается. Например, имеется два оператора условия:

IF X>0

THEN X=A

и

IF (X>0 & FLAG=’1’B) !

(X=0) & FLAG=’0’B)

THEN X=A;

ELSE;

Оба оператора предполагают единственное ветвление и могут быть представлены одним и тем же графом рис.3. Очевидно, цикломатическое число будет для обоих операторов одинаковым, не отражающим сложности предикатов, что весьма существенно при оценке программ.

Исходя из этого, Г. Майерс предложил расширение этой метрики. Суть подхода Г. Майерса состоит в представлении метрики сложности программ в виде интервала [z(G),z(G)+h]. Для простого предиката h=0 для n-местных предикатов h=n-1. Таким образом, первому оператору соответствует интервал [2,2], а второму [2,6].

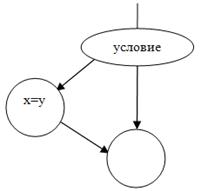
Рис 2.Граф ветвления

Большой интерес представляет оценка сложности программ по методу граничных значений.

Введем несколько дополнительных понятий, связанных с графом программы.

Пусть 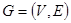– ориентированный граф программы с единственной начальной и единственной конечной вершинами. В этом графе число входящих в вершину дуг называется отрицательной степенью вершины, а число исходящих из вершины дуг – положительной степенью вершины. Тогда набор вершин графа можно разбить на две группы: вершины, у которых положительная степень ≤1; вершины, у которых положительная степень ≥2.

Вершины первой группы назовем принимающими вершинами, а вершины второй - вершинами отбора.

Для получения оценки по методу граничных значений необходимо разбить граф G на максимальное число подграфов G', удовлетворяющих следующим условиям: вход в подграф осуществляется только через вершину отбора; каждый подграф включает вершину (называемую в дальнейшем нижней границей подграфа), в которую можно попасть из любой другой вершины подграфа. Например, вершина отбора соединенная сама с собой дугой-петлей, образует подграф (рис. 3, табл.1).

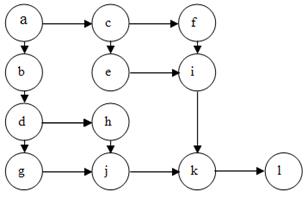
Рис. 3. Граф программы для анализа ее сложности методом граничных значений

Число вершин, образующих такой подграф, равно скорректированной сложности вершины отбора.

Таблица 1. Подграфы программы

Таблица 2. Скорректированная сложность вершин графа программы

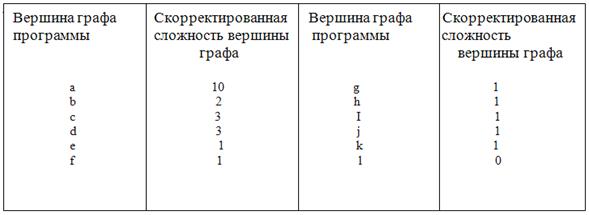
Каждая принимающая вершина имеют скорректированную сложность, равно 1, кроме конечной вершины, скорректированная сложность которой равна 0. Скорректированные сложности всех вершин графа G суммируются, образуя абсолютную граничную сложность программы. После этого определяется относительная граничная сложность программы:

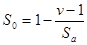, (8)

где 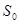– относительная граничная сложность программы; 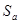– абсолютная граничная сложность программы; 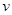– общее число вершин графа программы.

Таким образом, относительная граничная сложность программы равна 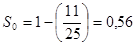. Преимущество метода граничных значений состоит в его чувствительности к конструктивному контексту программ. Это иллюстрирует пример (рис.5).

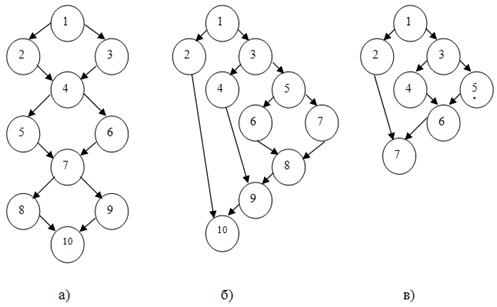
Рис. 5. Графы программ с одинаковым цикломатическим числом.

Приведенные на рис. 5. графы программ имеют следующие характеристики: циклическое число Маккейба Z(G); расширение Майерса для цикломатического числа Z’(G); количество точек пересечения; методику Джилба CL; относительную методику Джилба cl; уровень вложенности операторов условия CLI; метод граничных значений .

Таблица 3. Сравнение метрик сложности потока управления программ

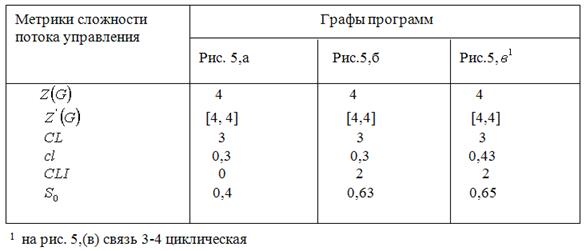
Полученные нами статистические данные наиболее показательны как раз для этой группы метрик и свидетельствуют о том, что оценку сложности программы, нельзя получить на основании какой-либо одной характеристики.

К вариантам цикломатической меры сложности относят также меру Чена

М(G) = (V(G),C,Q),

где С – количество условий, необходимых для покрытия управляющего графа минимальным числом маршрутов, а Q – степень связности структуры графа программы и ее протяженность.

Топологическая мера Чена выражает сложность программы числа пересечений границ между областями, образуемыми блок – схемой программы. Этот подход применим только к структурированным программам, допускающим лишь последовательное соединение управляющих конструкций. Для неструктурированных программ мера Чена существенно зависит от условных и безусловных переходов. В этом случае можно указать верхнюю и нижнюю границы меры. Верхняя – есть m+1, где m – число логических операторов при их гнездовой вложенности. Нижняя – равна 2. Когда управляющий граф программы имеет только одну компоненту связности, мера Чена совпадает с цикломатической мерой Маккейба.

Мера Пивоварского ставит целью учесть в оценке сложности ПО различия не только между последовательными и вложенными управляющими конструкциями, но и между структурированными и неструктурированными программами. Она выражается отношением

N(G) = n *(G) + S Pi,

где n *(G) – модифицированная цикломатическая сложность, вычисленная так же, как и V(G), но с одним отличием: оператор CASE с n- выходами рассматривается как один логический оператор, а не как n – 1 операторов. Рi – глубина вложенности i – той предикатной вершины. Для подсчета глубины вложенности предикатных вершин используется число сфер влияния. Под глубиной вложенности понимается число всех сфер влияния предикатов, которые либо полностью содержатся в сфере рассматриваемой вершины, либо пересекаются с ней. Глубина вложенности увеличивается за счет вложенности не самих предикатов, а сфер влияния. Сравнительный анализ цикломатических и функциональных мер с обсуждаемой для десятка различных управляющих графов программы показывает, что при нечувствительности прочих мер этого класса, мера Пивоварского возрастает при переходе от последовательных программ к вложенным и далее к неструктурированным.

Задание по работе

Оформить отчет по работе согласно заданному варианту, привести словесное описание алгоритма, приложить листинг программы с комментариями и выводы.

Вариант 1

Оценить сложность программы вычислив цикломатическое число Маккейба z(G) (цикломатическая сложность графа программы):

z(G)=e-v+2p,

где е – число дуг ориентированного графа Q; v – число вершин; р – число компонентов связности графа.

Вариант 2

Оценить сложность программы используя расширение метрики Маккейба (подход Майерса – представлении метрики сложности программ в виде интервала [z(G),z(G)+h].).

Вариант 3

Оценка качества программ по метрике Чена

M(G) = (z(G), C, Q),

где z(G) – цикломатическая сложность Маккейба,

С – количество условий, необходимых для покрытия управляющего графа минимальным числом маршрутов,

Q – степень связности структуры программы и ее протяженности.

Вариант 4

Оценка качества программ по метрике Пивоварского:

N(G) = z*(G) + ,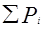

где z*(G) – модифицированная цикломатическая сложность, вычисленная так же, как и z(G), но с одним отличием:

оператор Case с n- выходами рассматривается как один логический оператор, а не как n – 1 операторов.

Pi – глубина вложенности i – ой предикатной вершины.

Вариант 5

Оценка качества программ по метрике Шнадевида (число путей в управляющем графе)

S =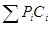

где Pi – глубина вложенности i-ой предикатной вершины.

С – количество условий, необходимых для покрытия управляющего графа минимальным числом маршрутов.

Вариант 6

Оценка сложности программ по методу граничных значений.

Контрольные вопросы

1) Назвать метрики, которые являются представителями группы метрик сложности потока управления программ.

2) Что такое управляющий граф программы?

3) Что такое цикломатическая сложность графа?

4) Что такое сильносвязный граф?

5) Что такое "модифицированная" цикломатическая сложность графа?

6) Суть подхода Г.Майерса к расширению метрики Маккейба.

7) Оценка сложности программ по методу граничных значений.

8) Что такое отрицательная и положительная степени вершины графа.

9) Какие метрики можно отнести к вариантам цикломатической меры сложности программ?

10) С помощью какой метрики можно посчитать число путей в управляющем графе?

Лабораторная работа № 4. Разработка программ оценки сложности ПО на базе отдельных метрик сложности программ - метрик сложности потока данных

Цель работы:изучить метрики сложности потока данных программ.