Приближение равной вероятности символов в тексте

Количество информации как мера уменьшения неопределенности знания

Получение информации можно связать с уменьшением неопределенности знания. Это позволяет количественно измерять информацию, что чрезвычайно важно для информатики. Рассмотрим вопрос об определении количества информации более подробно на конкретных примерах.

Пусть у нас имеется монета, которую мы бросаем на ровную поверхность. С равной вероятностью произойдет оно из двух возможных событий – монета окажется в одном из двух положений: «орел» или «решка».

Можно говорить, что события равновероятны, если при возрастающем числе опытов количества выпадений «орла» и «решки» постепенно сближается. Например, если мы бросим монету 10 раз, то «орел» может выпасть 7 раз, а «решка» – 3 раза, если бросим монету 100 раз, то «орел» может выпасть 60 раз, а «решка» – 40 раз, если бросим монету 1000 раз, то «орел» может выпасть 520 раз, а «решка» – 480 и т.д. В итоге при очень большой серии опытов количества выпадений «орла» и «решки» практически сравняются.

Перед броском существует неопределенность нашего знания (возможны два события), и как упадет монета, предсказать невозможно. После броска наступает полная определенность, так как мы видим (получаем зрительное сообщение), что монета в данный момент находится в определенном положении (например, «орел»). Это сообщение приводит к уменьшению неопределенности нашего знания в два раза, так как из двух возможных равновероятных событий реализовалось одно.

Чем больше количество возможных событий, тем больше начальная неопределенность нашего знания и соответственно тем больше количество информации будет содержать сообщение о результатах опыта.

Единицы измерения количества информации

За единицу количества информации принимается такое количество информации, которое содержит сообщение, уменьшающее неопределенность знания в два раза. Такая единица названа бит.

Минимальной единицей измерения информации является бит, а следующей по величине единицей – байт, причем

1 байт = 2³ бит = 8 бит

Так кратные байту единицы измерения количества информации вводятся следующим образом:

1Кбайт = 2¹⁰ байт = 1024 байт;

1Мбайт = 2¹⁰ Кбайт = 1024 Кбайт;

1Гбайт = 2¹⁰ Мбайт = 1024 Мбайт;

1Терабайт (Тб) = 2¹⁰ Гбайт =1024 Гбайт;

1Петабайт (Пб) = 2¹⁰ Тбайт = 1024 Тбайт.

Практическое задание(Босова Л. Л., 8 кл.)

1. Выразите объем информации в различных единицах, заполняя таблицу:

Бит	Байт	Кбайт
215
		23

2. Расположите величины в порядке убывания: 1024 бита, 1000 байтов, 8 бит, 1 байт, 10 Кбайт.

3. Расположите величины в порядке возрастания: 1010 байтов, 2 байта, 1 Кбайт, 20 битов, 10 битов.

4. Сколько Кбайт информации содержит сообщение следующего объема: 2¹⁶ битов, 2¹⁶ байтов, ¼ Мбайт, 1/512 Гбайт?

5. Информационный объем одного сообщения составляет 0,5 Кбайт, а другого – 500 байтов. На сколько битов информационный объем первого сообщения больше объема второго сообщения?

6. Информационный объем одного сообщения составляет 0,5 Кбайт, а другого – 128 битов. Во сколько раз информационный объем первого сообщения больше объема второго сообщения?

7. Заполните пропуски (степени двойки).

1 байт	23 битов
1 Кбайт	2— битов	210 байтов
1 Мбайт	2— битов	2— байтов	210 Кбайт
1 Гбайт	2— битов	2— байтов	2— Кбайт	210 Мбайт
1 Тбайт	2— битов	2— байтов	2— Кбайт	2— Мбайт	210 Гбайт
1 Пбайт	2— битов	2— байтов	2— Кбайт	2— Мбайт	2— Гбайт	210 Тбайт

8. Найдите х.

а) 8^х битов = 32 Кбайт; б)16^х битов = 128 Кбайт.

Формула Хартли

В 1928 г. американский инженер Р. Хартли предложил научный подход к оценке сообщений. Предложенная им формула имела следующий вид:

I = log₂ N ,

Где N - количество равновероятных событий; I - количество бит в сообщении, такое, что любое из N событий произошло. Тогда N =2^I.

Иногда формулу Хартли записывают так:

I = log₂ N = log₂ (1 / р) = - log₂ р,

т. к. каждое из К событий имеет равновероятный исход р = 1 / N, то К = 1 / р.

Формула Шеннона

Существует множество ситуаций, когда возможные события имеют различные вероятности реализации. Например, если монета несимметричная (одна сторона тяжелее другой), то при ее бросании вероятности выпадения «орла» и «решки» будут различаться.

Формулу для вычисления количества информации для событий с различными вероятностями предложил К. Шеннон в 1948 году. В этом случае количество информации определяется по формуле:

,

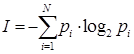где I - количество информации,

N – количество возможных событий,

p_i – вероятности отдельных событий.

Для частного, но широко распространенного и рассматриваемого выше случая, когда события равновероятны (p_i = 1/N), величину информации I можно рассчитать по формуле:

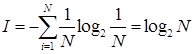
Практическое задание «Бросание пирамидки».Определить количество информации, которую мы получаем в результате бросания несимметричной и симметричной пирамидок.

При бросании несимметричной четырехгранной пирамидки вероятности отдельных событий равны: p₁ =1/2, p₂ = 1/4 , p₃ = 1/8, p₄ = 1/8.

Количество информации, которую мы получим после бросания несимметричной пирамидки, можно рассчитать по формуле :

I = - (1/2· log₂1/2 + 1/4·log₂1/4 + 1/8·log₂1/8 + 1/8·log₂1/8) бит = (1/2·log₂2 + 1/4·log₂4 + 1/8·log₂8 + 1/8·log₂8) бит = (1/2 + 2/4 + 3/8 +3/8) бит = 14,8 бит = 1,75 бит.

При бросании симметричной четырехгранной пирамидки вероятности отдельных событий равны между собой: p₁ = p₂ = p₃ = p₄ = 1/4.

Количество информации, которую мы получим после бросании симметричной пирамидки, можно рассчитать по формуле: I = log₂4 = 2 бита.

Таким образом, при бросании симметричной пирамидки, когда события равновероятны, мы получим большее количество информации (2 бита), чем при бросании несимметричной пирамидки, когда события неравновероятны (1,75 бита).

Выбор правильной стратегии в игре «угадай число». На получение максимального количества информации строится выбор правильной стратегии в игре «Угадай число», в которой первый участник загадывает целое число (например, 3) из заданного интервала (например, от 1 до 16), а второй должен «угадать» задуманное число. Если рассмотреть эту игру с информационной точки зрения, то начальная неопределенность знания для второго участника составляет 16 возможных событий (вариантов загаданных чисел).

При правильной стратегии интервал чисел всегда должен делиться пополам, тогда количество возможных событий (чисел) в каждом из полученных интервалов будет одинаково и их отгадывание равновероятно. В этом случае на каждом шаге ответ первого игрока («Да» или «Нет») будет нести максимальное количество информации (1 бит).

Как видно из таблицы, угадывание числа 3 произошло за четыре шага, на каждом из которых неопределенность знания второго участника уменьшалась в два раза за счет получения сообщения от первого участника, содержащего 1 бит информации. Таким образом, количество информации, необходимой для отгадывания одного из 16 чисел, составило 4 бита.

Информационная модель игры «Угадай число»

Вопрос второго участника	Ответ первого участника	Неопределенность знания (количество возможных событий)	Полученное количество информации
Число больше 8?	Нет		1 бит
Число больше 4?	Нет		1 бит
Число больше 2?	Да		1 бит
Это число 3?	Да		1 бит

Практическое задание «Определение количества информации».

В непрозрачном мешочке хранятся 10 белых, 20 красных, 30 синих и 40 зеленых шариков. Какое количество информации будет содержать зрительное сообщение о цвете вынутого шарика?

Так как количество шариков различных цветов неодинаково, то вероятности зрительных сообщений о цвете вынутого из мешочка шарика также различаются и равны количеству шариков данного цвета, деленному на общее количество шариков: p_б = 0,1 ; p_к = 0,2; p_з =0,3; p_с= 0,4

События неравновероятны, поэтому для определения количества информации, содержащейся в сообщении о цвете шарика, воспользуемся формулой: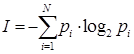

I = - (0, 1·log₂ 0, 1 + 0,2· log₂ 0,2 + 0,3· log₂0,3 + 0,4· log₂0,4) = 1,85 бита

Практическое задание «Определение количества информации в тексте».Система оптического распознавания символов позволяет преобразовать отсканированные изображения страниц документа в текстовой формат со скоростью 4 страницы в минуту и использует алфавит мощностью 65 536 символов. Какое количество информации будет нести текстовый документ, каждая страница которого содержит 40 строк по 50 символов, после 10 минут работы приложения?

По формуле: N = 2ⁱ определим информационную емкость символа алфавита: 65536 = 2ⁱ => 2¹⁶ = 2ⁱ => I = 16 бит.

По формуле: I_c = I·К определим количество информации на странице: 16 бит·40·50 = 32000 бит = 4000 байт.

Определим количество информации, которое будет нести текстовый документ: 4000 байт·4·10 = 160000 байт. 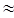156 Кбайт.

Алфавитный подход

Алфавитный подход используется для измерения количества информации в тексте, представленном в виде последовательности символов некоторого алфавита. Такой подход не связан с содержанием текста. Количество информации в этом случае называется информационным объемом текста, который пропорционален размеру текста – количеству символов, составляющих текст. Иногда данный подход к измерению информации называют объемным подходом.

Каждый символ текста несет определенное количество информации. Его называют информационным весом символа. Поэтому информационный объем текста равен сумме информационных весов всех символов, составляющих текст.

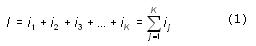
Здесь предполагается, что текст – это последовательная цепочка пронумерованных символов. В формуле (1) i₁обозначает информационный вес первого символа текста, i₂–информационный вес второго символа текста и т.д.; K –размер текста, т.е. полное число символов в тексте.

Все множество различных символов, используемых для записи текстов, называется алфавитом. Размер алфавита – целое число, которое называется мощностью алфавита. Следует иметь в виду, что в алфавит входят не только буквы определенного языка, но все другие символы, которые могут использоваться в тексте: цифры, знаки препинания, различные скобки, пробел и пр.

Определение информационных весов символов может происходить в двух приближениях:

1) в предположении равной вероятности (одинаковой частоты встречаемости) любого символа в тексте;

2) с учетом разной вероятности (разной частоты встречаемости) различных символов в тексте.

Приближение равной вероятности символов в тексте

Если допустить, что все символы алфавита в любом тексте появляются с одинаковой частотой, то информационный вес всех символов будет одинаковым. Пусть N – мощность алфавита. Тогда доля любого символа в тексте составляет 1/N-ю часть текста. По определению вероятности эта величина равна вероятности появления символа в каждой позиции текста:

p = 1/N

Согласно формуле К. Шеннона, количество информации, которое несет символ, вычисляется следующим образом:

i = log2(1/p) = log2N (бит) (2)

Следовательно, информационный вес символа (i) и мощность алфавита (N) связаны между собой по формуле Хартли 2ⁱ = N.

Зная информационный вес одного символа (i) и размер текста, выраженный количеством символов (K), можно вычислить информационный объем текста по формуле:

I = K · i (3)

Эта формула есть частный вариант формулы (1), в случае, когда все символы имеют одинаковый информационный вес.

Из формулы (2) следует, что при N = 2 (двоичный алфавит) информационный вес одного символа равен 1 биту.

С позиции алфавитного подхода к измерению информации 1 бит– это информационный вес символа из двоичного алфавита.

Более крупной единицей измерения информации является байт.

1 байт– это информационный вес символа из алфавита мощностью 256.

Поскольку 256 = 2⁸, то из формулы Хартли следует связь между битом и байтом:

2ⁱ = 256 = 2⁸

Отсюда: i = 8 бит = 1 байт

Для представления текстов, хранимых и обрабатываемых в компьютере, чаще всего используется алфавит мощностью 256 символов. Следовательно, 1 символ такого текста “весит” 1 байт.

Задачи

Пример 1.Сколько различных символов, закодированных байтами, содержится в сообщении:

1101001100011100110100110001110001010111?

Решение:Разбиваем сообщение на восьмёрки битов (то есть, на байты):

11010011 00011100 11010011 00011100 01010111.

Сравнивая байты между собой, видим, что первый и третий, а также второй и четвёртый байты одинаковые. Следова­тельно, различных символов всего три.

Пример 2.Для записи письма был использован алфавит мощностью в 16 символов. Письмо состояло из 25 строк. В каждой строке вместе с пробелами было 64 символа. Сколько байт информации содержало письмо?

Решение:М = 16

i = lоg₂16 = 4 (бит)

К = 25*64= 1600

I = К*i = 1600 * 4 бит = 6400 бит = 800 байт

Ответ: 800 байт.

Пример 3. Письмо состояло из 30 строк. В каждой строке вместе с пробелами по 48 символов. Письмо содержало 900 байт ин­формации. Какова мощность алфавита (количество символов), которым было написано письмо?

Решение:

К = 30*48 =1440

I = 900 байт = 7200 бит

i = I/К = 5 бит

N = 2⁵ = 32 символа

Ответ: 32 символа.

Пример 4. Даны два текста, содержащих одинаковое количество символов. Первый текст состоит из алфавита мощностью 16 символов, а второй текст - из 256 символов. Во сколько раз информации во втором тексте больше, чем в первом?

Решение:

К₁ = К₂

N₁ = 16, N₂ = 256

i₁ = lоg₂16 = 4 (бит)

i₂ = lоg₂256 = 8(бит)

I₁=К₁* i_{1 ,} I₂=К₂* i₂

I₂/I₁= (К₂*i₂) / (К1* i₁) = (К₂*8) / (К₂*4) =8/4 = 2

Ответ: в 2 раза.

Пример 5. Каждый символ в Unicode закодирован двухбайтным словом. Оцените информационный объем следующего предложения в той кодировке:

«Без труда не вытащишь рыбку из пруда.»

1)37 бит 2) 592 бита 3) 37 байт 4) 592 байта

Решение:

Длина фразы составляет примерно 40 символов. Следовательно, ее объем можно приблизительно оценить в 40 ´ 2 =80 байт. Такого варианта ответа нет, попробуем перевести результат в биты: 80 байт ´ 8 = 640 бит. Наиболее близкое значение из предложенных — 592 бита. Заметим, что разница между 640 и 592 составляет всего 48/16 = 3 символа в заданной кодировке и его можно считать несущественным по сравнению с длиной строки.

Ответ: 2.

Замечание: Подсчетом символов в строке можно убедиться, что их ровно 37 (включая точку и пробелы), поэтому оценка 592 бита = 74 байта, что соответствует ровно 37 символам в двухбайтовой кодировке, является точной.

Пример 6. Метеорологическая станция ведет наблюдение за влажностью воздуха. Результатом одного измерения является целое число от 0 до 100%, которое записывается при помощи минимально возможного количества бит. Станция сделала 80 измерений. Определите информационный объем результатов наблюдений.

1) 80 бит 2) 70 байт 3) 80 байт 4) 560 байт

Решение:

Способ 1

Воспользуемся формулой алфавитного подхода к измерению количества информации I = M log₂N, где N — количество символов (мощность) алфавита, в котором записано сообщение, М — количество символов в записи сообщения (длина сообщения), I — количество бит информации, содержащееся в сообщении.

Алфавитом в данном случае является множество целочисленных значений влажности от 0 до 100. Таких значений 101. Поэтому информационный объем результатов одного измерения I=log₂101. Это значение не будет целочисленным. Не вычисляя его, сразу найдем округленное в большую сторону целое значение. Заметим, что ближайшая к 101 целая степень двойки, большая 101, есть число 128 = 2⁷. Поэтому принимаем 7=log₂128 = 7 бит. Учитывая, что станция сделала 80 измерений, общий информационный объем равен 80 ´ 7=560 бит =70 байт.

Ответ: 2.

Способ 2

Воспользуемся следствием из формулы. Заметим, что 2⁶< 101 < 2⁷, поэтому минимально необходимое количество двоичных разрядов (бит) равно 7. Далее аналогично получаем, что общий информационный объем равен 80 ´ 7 = 560 бит = 70 байт.

Ответ: 2.

Пример 7.Для регистрации на сайте некоторой страны пользователю требуется придумать пароль. Длина пароля – ровно 11 символов. В качестве символов используются десятичные цифры и 12 различных букв местного алфавита, причём все буквы используются в двух начертаниях: как строчные, так и заглавные (регистр буквы имеет значение!).

Под хранение каждого такого пароля на компьютере отводится минимально возможное и одинаковое целое количество байтов, при этом используется посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством битов.

Определите объём памяти, который занимает хранение 60 паролей.

1) 540 байт 2) 600 байт 3) 660 байт 4) 720 байт

Решение:

1) согласно условию, в пароле можно использовать 10 цифр (0..9) + 12 заглавных букв местного алфавита + 12 строчных букв, всего 10 + 12 + 12 = 34 символа

2) для кодирования 34 символов нужно выделить 6 бит памяти (5 бит не хватает, они позволяют закодировать только 2⁵ = 32 варианта)

3) для хранения всех 11 символов пароля нужно 11 × 6 = 66 бит

4) поскольку пароль должен занимать целое число байт, берем ближайшее большее (точнее, не меньшее) значение, которое кратно 8: это 72 = 9 × 8; то есть один пароль занимает 9 байт

5) тогда 60 паролей занимают 9 × 60 = 540 байт

Ответ: 1.