Реализация деревьев в динамической области памяти
Содержание
1. Описание предметной области - Цветочный магазин. 3
2. Описание выбранной динамической структуры.. 3
3. Устройство программы.. 10
4. Листинг программы.. 16
5. Протокол выполнения программы.. 26
6.Список используемой литературы.. 26
Описание предметной области - Цветочный магазин
В моей программе необходимо обработать базу данных, содержащую в себе названия цветов, поиски, вывод в файл. База данных построена с помощью списка и дерева. Поиск осуществляется в самом дереве. Все данные выводятся в файл под названием «Цветочный магазин.txt». Данные о магазине хранятся в оперативной области памяти, а их обработка происходит в динамической области памяти, с использованием иерархического типа данных – дерева. Программа обрабатывает данные текстового типа, с помощью операций: добавления данных, поиск и упорядочивание данных, сохранения данных в файл, вывод данных.
Описание выбранной динамической структуры
Хотя динамика и не является отличительной чертой языка Паскаль, все же существует возможность создавать динамические объекты и оперировать с ними. Динамический объект представляет собой область памяти без идентификатора. Для обращения к этой области заводится специальная ссылочная переменная, которая описывается в программе. Элементами множества значений ссылочного типа являются значения адресов оперативной памяти. Чаще всего динамические структуры состоят из объектов, являющихся записями из нескольких полей, одна или несколько из которых являются ссылками на такой же объект. Таким образом, можно составлять цепочки или более сложные структуры ссылающихся друг на друга объектов. Размер таких структур ограничивается только объемом свободной памяти и может легко меняться при удалении и создании объектов, что и определило основную область их применения – моделирование нелинейных последовательных структур данных (например, деревьев). Однако, несмотря на кажущееся отсутствие недостатков, динамические структуры тоже имеют свои минусы. Главный из них – отсутствие наглядности программы – вызывает трудности при создании особо крупных структур.
Представление абстрактных типов данных (АТД) в Паскале
Моделирование абстрактных типов данных на конкретных структурах данных Паскаля не является однозначным. Практически любой АТД может быть эффективным образом представлен как на массиве, так и на файле или на динамической структуре, но чаще всего конкретное представление диктуется особенностью доступа к элементам рассматриваемого абстрактного типа.
Иерархические (древовидные) структуры данных
Реализация деревьев в динамической области памяти
Дерево - это совокупность элементов, называемых узлами (при этом один из них определен как корень), и отношений (предок-потомок), образующих иерархическую структуру узлов. Узлы могут являться величинами любого простого или структурированного типа, за исключением файлового. Узлы, которые не имеют ни одного последующего узла, называются листьями. Каждая конечная древовидная структура содержит элемент, не имеющий вышестоящего. Этот элемент называется «корнем» или «корневым узлом». Он может считаться первым (или стартовым) узлом. Обратное утверждение, в общем случае, неверно: бесконечные древовидные структуры могут иметь, а могут и не иметь корневые узлы. Линии, связывающие элементы называются «ветвями», а сами элементы называются узлами. Узлы без потомков называются «конечными узлами» или «листьями». Названия связей между узлами именуются по принципу семейных взаимосвязей. На Западе в области информатики, в основном используются только названия членов семьи мужского рода, в русском языке для обозначения узла, напрямую связанного с узлом-родителем и находящимся в иерархии ниже, часто называют «дочерним». В лингвистике (англоязычной, к примеру), напротив, используются названия членов семей женского рода. Это свидетельствует о возврате к соглашению об общепринятых правилах наименования, авторами которого являются студентки известного американского лингвиста Ноама Хомского. Несмотря на это, в информатике нейтральные названия «родитель» и «дитя» часто заменяются словами «отец» и «сын», кроме того, термин «дядя» не менее активно используется для обозначения других узлов, находящихся на том же уровне, что и родитель.
- Узел является «родителем» другого узла, если он расположен на один шаг выше в иерархии дерева, то есть, находится ближе к корневому узлу.
- «Дети» («брат» или «сестра») имеют общий родительский узел.
- Узел, связанный со всеми нижележащими узлами называется «предком» или «предшественником».
Чаще всего деревья определяют рекурсивно:
Деревос базовымтипом Т –это:
· либо пустое дерево;
·
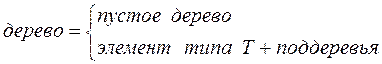 |
либо некоторая вершина типа Т с конечным числом связанных с ней
отдельных деревьев с базовым типом - Т, называемых поддеревьями.


Большой интерес в программировании представляют двоичные деревья.
Двоичное дерево – это упорядоченное дерево, каждая вершина которого имеет не более двух потомков, которые называются левым и правым поддеревом этой вершины корня.
Примеры двоичного дерева:
n генеалогическое дерево, где у каждого человека есть предки в лице отца и матери;
n схема теннисного турнира, где каждая игра – это вершина, обозначенная ее победителем, а предки – две предыдущие игры соперников;
n арифметическое выражение с бинарными операциями, где каждому оператору соответствует вершина, а операнды – поддеревья.
Часто для представления данных, среди которых идет поиск элементов по заданному ключу используют двоичное дерево, которое называется двоичным деревом поиска или сортированным деревом. Формируется это дерево по следующему правилу: ключевое поле левого поддерева всегда должно содержать значение меньше, чем в корне, а ключевое поле правого поддерева – значение больше или равное значению в корне.
Пример:
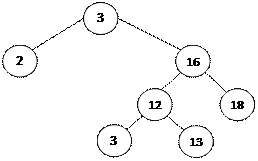 |
Вводится последовательность целых чисел {3, 16, 12, 2, 3, 18, 13}. Построить двоичное дерево поиска.
Существует три порядка обхода дерева:
| Порядок обхода | Обход дерева (см. Пример: ) |
| Слева направо(inorder): левое поддерево, вершина, правое поддерево. | {2, 3, 3, 12, 13, 16, 18} |
| Сверху вниз(preorder): вершина, левое поддерево, правое поддерево. | {3, 2, 16, 12, 3, 13, 18} |
| Снизу вверх (postorder): левое поддерево, правое поддерево, вершина. | {2, 3, 13, 12, 18, 16, 3} |
При этом обратите внимание, что обход слева направо дает неубывающую последовательность чисел, поэтому дерево поиска имеет второе название сортированное.
