Задача № 2: система Тьюринга

КУРСОВАЯ РАБОТА

по дисциплине: «Математическая логика и теория алгоритмов»

Проверил,

Ершов С.С.

2012 г.

Автор работы

студент группы

ПС

2012 г.

Курсовая защищена

с оценкой

2012 г.

Челябинск, 2012 г.

Оглавление

1 Задача № 1: Машина Поста

1.1. Контрольный пример ……………………………………………………………….….3

1.2. Идея решения задачи……………………………………………………………………3

1.3. Схема алгоритма

1.3.1. Крупная схема алгоритма…………………………………………………….....4

1.3.2. Детализированная схема алгоритма………………………………………….....5

1.4. Текст программы………………………………………………………………………..6

1.5. Анализ результатов……………………………………………………………………..6

2 Задача № 2: Машина Тьюринга

2.1. Контрольный пример……………………………………………………………….…..7

2.2. Идея решения задачи………………………………………………….………………...7

2.3. Граф состояний переходов...…………………………………………………………...8

2.4. Таблица состояний переходов………………………………………………………....9

2.5. Анализ результатов…………………………………………………………………..…9

Библиографический список……………………………………………………………..….….10

Задача № 1: Машина Поста

Для машины Поста составить программу, выполняющую умножение цифр «3» и «2».

1.1 Контрольный пример

Рисунок 1 отражает начальную конфигурацию. Рисунок 2 стандартную конечную конфигурацию.

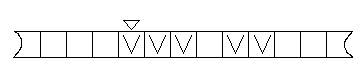
Рис. 1. Стандартная начальная конфигурация

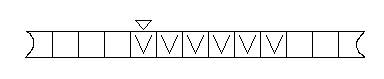
Рис. 2. Стандартная конечная конфигурация

1.2 Идея решения задачи

Идея решения состоит в том, что после нахождения конца группы меток, головка возвращается обратно, ставя метку в пустую ячейку между двумя группами меток. На каждом шаге, ячейка проверяется на наличие метки. При условии наличия метки в ячейке выполняется дальнейшее перемещение каретки вправо. В случае отсутствия метки, выполняется перемещение каретки на одну ячейку вправо. Если в следующей ячейке отсутствует метка, головка начинает движение в обратном направлении. В завершении работы алгоритма, на ленте, ставится метка между двумя, найденными, группами меток.

1.3. Схема алгоритма

1.3.1. Крупная схема алгоритма

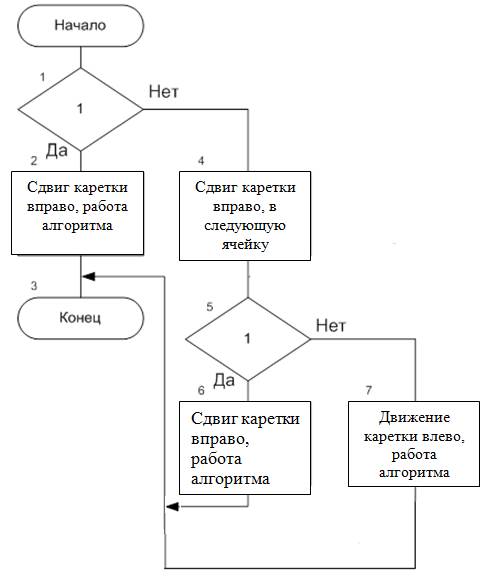
Рис. 3. Крупная схема алгоритма

1.3.2. Детализированная схема алгоритма

Конец

Ставим метку

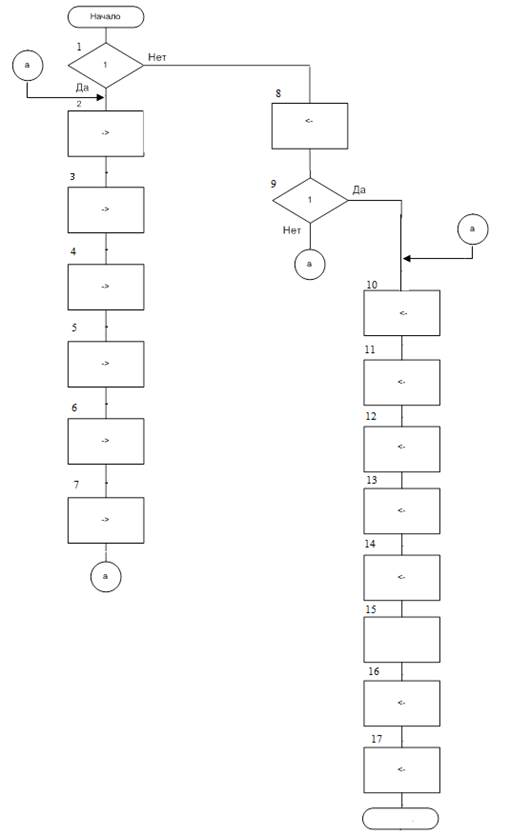
Рис. 4. Детализированная схема алгоритма

1.4 Текст программы

В детализированной схеме алгоритма 17 блоков, а значит, в программе будет 17 команд.

Сложение трёх целых чисел Таблица 1

Адрес	Операция	Адрес перехода (по 0 или безусловный)	Адрес перехода (по 1)
	Условный переход
	Шаг влево
	Шаг вправо
	Условный переход
	Шаг вправо
	Шаг вправо
	Шаг вправо
	Шаг вправо
	Шаг вправо
	Шаг влево
	Шаг влево
	Шаг влево
	Шаг влево
	Поставить метку
	Шаг влево
	Шаг влево
	Стоп

1.5 Анализ результатов

Разработанная программа весьма универсальна, так как она учитывает начальное положение головки не только над меткой, но и над пустой ячейкой. Размер программы получился сравнительно небольшой (16 команд).

Программа была написана, проверена и отлажена в системе POST 2002. Результаты тестов показывают правильность ее работы.

Задача № 2: система Тьюринга

Для машины Тьюринга составить программу, выполняющую вычитание чисел в троичной системе счисления.

1.

2.

2.1. Контрольный пример

В качестве примера возьмём цифры девять и пять, записанные в троичной системе счисления: 100 и 12.

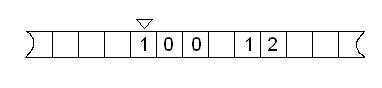
Рис. 5. Стандартная начальная конфигурация

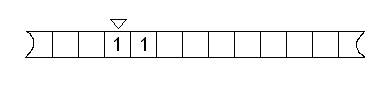
Рис. 6. Стандартная конечная конфигурация

2.2. Идея решения задачи

Идея решения состоит в том, что на ленте расположены числа, записанные в троичной системе счисления. Головка двигается до последней метки, со значением «2», обозначающей то, что чисел больше не будет (последняя метка), а затем возвращается, удаляя и перезаписывая метки, реализуя, вычитание в троичной системе счисления.

2.3. Граф состояний и переходов

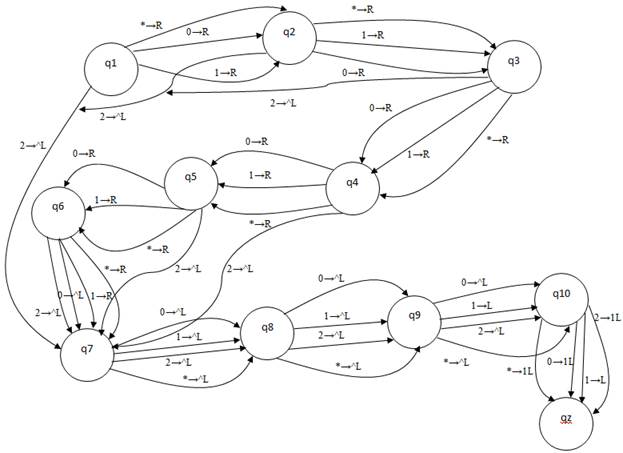
Рис. 6. Граф состояний и переходов программы

2.4. Таблица состояний и переходов

Вычитание чисел в троичной системе счисления Таблица 2

Состояние			*
q1	q2 R	q2 R	q2 R	q7 ^L
q2	q3 R	q3 R	q3 R	q7 ^L
q3	q4 R	q4 R	q4 R	q7 ^L
q4	q5 R	q5 R	q5 R	q7 ^L
q5	q6 R	q6 R	q6 R	q7 ^L
q6	q7 R	q7 R	q7 R	q7 ^L
q7	q8 ^L	q8 ^L	q8 ^L	q8 ^L
q8	q9 ^L	q9 ^L	q9 ^L	q9 ^L
q9	q10 ^L	q10 ^L	q10 ^L	q10 ^L
q10	q11 1L	q11 L	q11 ^L	q11 ^L
q11	qz 1L	qz L	qz 1L	qz 1L

1.5. Анализ результатов

Разработанная программа работает, вычитая числа в троичной системе счисления. Эта программа работает на практике. Она всегда дает точный и правильный результат. Размер программы получился достаточно небольшой ( операции).

Программа была написана, проверена и отлажена в системе MT. Результаты тестов показывают правильность её работы.
Библиографический список

1. Ершов С.С., Надточий И.Л., Самохвалов В.А. Прикладная математика: Учебное пособие по практическим занятиям.- Челябинск: ЧГТУ, 1992.

2. Успенский В.А. Машина Поста.- М.: Наука, 1979.

3. Ершов С.С. Элементы теории алгоритмов: Учебное пособие. Челябинск: Издательский центр ЮУрГУ, 2009.