Составление алгоритма решения. Представим алгоритм решения задачи одношаговой схемой без элементов организации дружественности (рис

Представим алгоритм решения задачи одношаговой схемой без элементов организации дружественности (рис. 7.6).

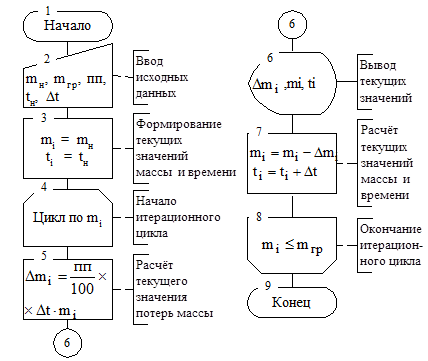
Рис. 7.6. Схема алгоритма задачи о сосульке

Программирование задачи

Программирование задачи требует следующей идентификации переменных (табл. 7.1).

Таблица 7.1

Обозначение в алгоритме	mн	mi	mгр	пп	tн	Dt	ti	Dmi
Обозначение в программе	mn	mi	mgr	pp	tn	dt	ti	dmi

Программы решения задачи по полученной схеме алгоритма с учетом таблицы идентификации переменных представлены ниже.

Классический вариант программирования задачи

#include <stdlib.h> /* директивы */

#include <stdio.h> /* препроцессора */

#include <conio.h>

#include <windows.h>:

void main()

{

float mn, mi, mgr,

pp, tn, dt, dmi,ti; /*описание переменных*/

char buf[50]; /*описание символьного массива*/

CharToOem("\n Введите начальную массу сосульки, кг : ", buf);

printf(buf);

scanf("%f", &mn);

CharToOem("\n Введите граничную массу сосульки, кг:", buf);

printf(buf);

scanf("%f", &mgr);

CharToOem("\n Введите потери массы, %/ч : ",buf);

printf(buf);

scanf("%f", &pp);

CharToOem("\n Введите начальное время таяния, ч : ",buf);

printf(buf);

scanf("%f", &tn);

CharToOem("\n Введите шаг времени, ч : ",buf);

printf(buf);

scanf("%f", &dt);

printf("\n ------------------------------"

"\n | ti | dmi | mi |"

"\n ------------------------------");

mi=mn; /*формирование текущего значения массы*/

ti=tn; /*формирование текущего значения времени*/

do

{

dmi = pp * mi * dt / 100; /*расчет текущих потерь */

printf( "\n | %4.2f | %6.4f | %6.4f |", ti, dmi, mi);

mi = mi - dmi; /*расчет текущей массы */

ti = ti + dt; /*расчет текущего времени */

}

while( mi >= mgr ); /*условие повторения цикла*/

printf("\n ------------------------------");

getch();

}

5 1 10 0 1.5 – исходные данные для решения задачи.

Результаты решения представлены в приложении 7.1.

Программирование задачи с графическим интерфейсом

Программирование задачи при использовании графического интерфейса предварим его разработкой.

ListBoxMp

ListBoxTi

ListBoxMi

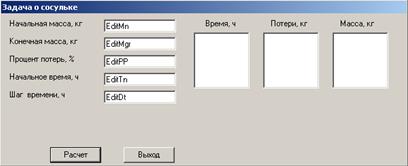
Для ввода начального и граничного значения массы сосульки планируем однострочные поля редактирования (EditMn и EditMgr). Процент потерь, начальное время и шаг времени предусматриваем вводить в однострочные поля редактирования (EditPP, EditTn и EditDt). Под вывод расчетных значений текущих значений времени, потерь массы и массы сосульки планируем поля-списки (ListBoxTi, ListBoxMp и ListBoxMi).

Управление процессом решения реализуем двумя командными кнопками, расположенными в нижней части окна. Назначение каждой определяется ее названием.

С учетом планируемого интерфейса выполним программирование задачи.

#include <stdlib.h> /* директивы */

#include <stdio.h> /* препроцессора */

…

ListBoxMp

ListBoxTi

ListBoxMi

void TSosulDlgClient::BNClickedOk()

{

// INSERT>> Your code here.

float mn, mi, mgr,

pp, tn, dt,dmi,ti; /*описание переменных*/

char buf[10]; /*описание символьного массива*/

ListBoxTi->ClearList(); /*Очистка */

ListBoxMp->ClearList(); /* полей */

ListBoxMi->ClearList(); /*вывода */

EditMn->GetText(buf,10); /* ввод начальной */

mn=atof(buf); /* массы сосульки*/

EditMgr->GetText(buf,10); /* ввод граничной */

mgr=atof(buf); /* массы сосульки*/

EditPP->GetText(buf,10); /* массы процента*/

pp=atof(buf); /* потерь*/

EditTn->GetText(buf,10); /* ввод начального */

tn=atof(buf); /* времени */

EditDt->GetText(buf,10); /* ввод шага */

dt=atof(buf); /* времени */

mi=mn; /*формирование текущего значения массы*/

ti=tn; /*формирование текущего значения времени*/

do

{

dmi = pp * mi *dt / 100; /*расчет текущих потерь */

sprintf(buf,"%5.3f",ti); /* вывод текущего */

ListBoxTi->AddString(buf); /* времени */

sprintf(buf,"%10.7f",dmi); /* вывод текущих */

ListBoxMp->AddString(buf); /* потерь */

sprintf(buf,"%10.7f",mi); /* вывод текущей */

ListBoxMi->AddString(buf); /* массы */

mi = mi - dmi; /*расчет текущей массы */

ti = ti + dt; /*расчет текущего времени */

}

while( mi >= mgr ); /*условие повторения цикла*/

}

5 1 10 0 1.5 – исходные данные для решения задачи.

Результаты решения представлены в приложении 7.2.

Внимание! Здесь и далее выделенные курсивом строки создателем программы не пишутся. Они формируются автоматически ИСРП в процессе машинной обработки программы.

Математические задачи

Математические вычисления, обеспечивающие достижение (превышение) заданной границы счета иллюстрируются задачей (7.2) расчета ряда Фибоначчи.

Ряд Фибоначчи – последовательность целых положительных чисел, начиная с 0 и 1, организованных таким образом, что каждое следующее число равно сумме двух предыдущих.

Постановка задачи

Рассчитать числа Фибоначчи (в порядке увеличения) до достижения трёхзначного значения.