Линейный двусвязный список

Свободен от недостатка, присущего односвязному списку. Для этого в каждое звено добавлен еще один указатель, значение которого - адрес предыдущего звена списка. Структура списка будет выглядеть следующим образом:

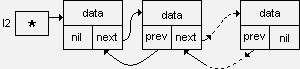
Преимущества двусвязного списка:

проще перестраивать поврежденный список;

проще выполняются некоторые операции (например удаление).

Кольцевые списки

Если значение указателя последнего звена линейного односвязного списка заменить с nil на адрес заглавного звена, то линейный список превратится в односвязный кольцевой список.

Для двусвязного списка, кроме того, нужно заменить с nil на адрес последнего звена значение второго указателя в заглакном звене. Получится двусвязный кольцевой (циклический) список.

В односвязном кольцевом списке можно переходить от последнего звена к заглавному, а в двусвязном - еще и от заглавного к последнему.

Программа работы с двусвязным списком на языке "Паскаль"

rel2=^elem2;

elem2=record

next:rel1;

prev:rel2;

data:<Тип хранимых данных>

end;

list2=rel2;

var

l2:list2;

procedure insert2(pred:rel2; info:<Тип>);

var

q:rel2;

begin

new(q); {Создание нового звена}

q^.data:=info;

q^.next:=pred^.next;

q^.prev:=pred^.next^.prev;

pred^.next.prev:=q;

pred^.next:=q

end;

procedure delete2(del:rel2);

begin

del^.next^.prev:=del^.prev;

del^.prev^.next:=del^.next;

dispose(del);

end;

function search2(list:rel2; info:<Тип>; var point:rel2):boolean;

var

p,q:rel2;

b:boolean;

begin

b:=false;

point:=nil;

p:=list;

q:=p^.next;

while (p<>q) and (not b) do

begin

if q^.data=info then

begin

b:=true;

point:=q

end;

q:=q^.next

end;

search2:=b

end;

...

...

...

var

l2:list2;

r:rel2;

begin {Создание заглавного звена}

new(r);

r^.next:=r;

r^.pred:=r;

l2:=r;

...

...

...

end.

Двусвязный кольцевой список выглядит так:

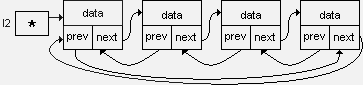
Кольцевой список, как и линейный, как единый программный объект идентифицируется указателем, например l2, значение которого - адрес заглавного звена.

Возможен другой вариант организации кольцевого списка:

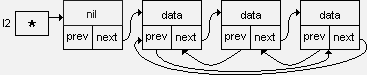
Первый вариант - проще выполняется вставка нового элемента как в начало списка (после заглавного звена), так и в конец - так как вставка звена в конец кольцевого списка эквивалентна вставке перед заглавным звеном.

Но каждый раз при циклической обработке списка нужно проверять, не является ли текущее звено заглавным.

Второй вариант - проверка текущего звена не требуется, но труднее выполнять добавление звена в конец списка.

Для двусвязного кольцевого списка: Операции вставки, удаления, поиска (для первого варианта). При вставке в начало списка (после заглавного звена) нужно указать в качестве pred адрес заглавного звена, то есть указатель на список (l2).

Возможность перемещаться по двусвязному списку в каждом направлении позволяет напрямую задавать удаляемое звено его адресом (указателем), следовательно, упрощаются процедуры удаления.

Для двусвязного списка возможны различные варианты поиска: от 1-го к N-му, от N-го к 1-му, от 1-го к N-му и обратно, и пр. Для кольцевого списка нужно учесть, что формально последнего звена нет.

Единообразие обработки всех звеньев списка, начиная с 1-го до N-го, достигается наличием заглавного звена списка. Его создание для односвязного списка можно осуществить следующим образом:

var a,l1:list1;

begin

...

new(l1);

l1^.next:=nil;

a:=l1;

...

Для двусвязного списка создание заглавного звена производится аналогично, за исключением двух указателей вместо одного.

Поиск

Одно из наиболее часто встречающихся в программировании действий – поиск. Существует несколько основных вариантов поиска, и для них создано много различных алгоритмов. При дальнейшем рассмотрении делается принципиальное допущение: группа данных, в которой необходимо найти заданный элемент, фиксирована. Будет считаться, что множество из N элементов задано в виде такого массива

a: array[0..N–1] of Item

Обычно тип Item описывает запись с некоторым полем, играющим роль ключа. Задача заключается в поиске элемента, ключ которого равен заданному «аргументу поиска» x. Полученный в результате индекс i, удовлетворяющий условию а[i].key = x, обеспечивает доступ к другим полям обнаруженного элемента. Так как здесь рассматривается, прежде всего, сам процесс поиска, то мы будем считать, что тип Item включает только ключ.

Поиск требуемой информации применяется ко всем основным структурам данных с произвольным доступом: массивам, спискам (одно- и двусвязным), таблицам, деревьям.

Последовательный поиск

Нахождение информации в неотсортированной структуре данных, например в массиве, требует применения последовательного поиска.

Последовательный поиск - наиболее просто реализуемый метод поиска.

Последовательный поиск заключается в последовательном просмотре массива от начального элемента до нахождения совпадения или до конца массива.

Пример - циклы for и while.

Последовательный поиск в среднем случае выполнит проверку 1/2*N элементов, в лучшем - 1 элемента, а в худьшем - N элементов.

Недостаток - медленное выполнение при большом объеме просматриваемого массива.

Но если данные не отсортированы, то должен использоваться только последовательный поиск.

Программалинейного поиска на языке "Паскаль"

var

nums:array[0..N] of real;

function search_s1(item:^real; n:integer; key:real):integer;

var

i:integer;

begin

for i:=0 to N do

if key=item[i] then

begin

search_s1:=i;

break

end

else

search_s1:=-1

end;

function search_s2(item:^real; n:integer; key:real):integer;

var

i:integer;

begin

i:=0;

search_s2:=-1;

while (key<>item[i]) or (i<n) do

begin

if key=item[i] then

search_s2:=i;

i:=i+1

end

end;

Двоичный поиск

Бинарный поиск основан на итерационном сравнении ключа поиска со средним элементом массива.

При каждой итерации интервал анализа делится пополам (на 2): 1/2, 1/4, 1/8 и т.д., откуда этот метод поиска и получил свое название. В зависимости от результата сравнения, выбирается нижний или верхний интервал. Процесс продолжается до тех пор, пока не будет найдено совпадение или длина интервала анализа не станет равной единице, и если при этом нет совпадения, то фиксируется неудача поиска.

Этот метод поиска значительно эффективнее чем последовательный поиск, но требует, чтобы данные были предварительно упорядочены (отсортированы).

В худшем случае выполняется не более log2(N)+E (где E<0.0861) сравнений, в связи с чем еще называется "логарифмическим поиском". Двоичный поиск также называется "дихотомическим".

Программа двоичного поиска на языке "Паскаль"

function search_b(item:^real; n:integer; key:real):integer;

var

low,high,mid:integer;

begin

search_b:=-1;

low:=0;

high:=n-1;

while low<=high do

begin

mid:=(low+high)/2;

if key<item[mid] then

hig:=mid-1

else

if key>item[mid] then

low:=mid+1

else

search_b:=mid

end

end;

Существуют модификации алгоритма:

с двумя переменными вместо low, high, mid (нижней, верхней границы и середины интервыла анализа) - текущее положение и величина его изменения. Такой метод требует аккуратности;

алгоритм со вспомогательными таблицами.

Поиск с использованием чисел Фибоначи. Числа Фибоначи используются вместо степеней двойки при делении интервала. В данном случае вместо деления используются только сложение и вычитание. Для этого требуется таблица чисел Фибоначи, или процедура их вычисления, исходя из длины интервала. Данный метод проще реализуется при N+1=Fk.

Интерполяционный поиск произошел от естественного поиска данных в упорядоченном массиве человеком. Если известно, что k находится между kl и kh, то следующее сравнение делается на расстоянии (l-k)(k-kl)/(kh-ki) от li. Предполагается что данные в массиве возрастают в арифметической прогрессии.

Этот алгоритм эффективнее бинарного поиска только в случае арифметической прогрессии, так как на каждом шаге уменьшает интервал анализа не до n/2 а до sqr(ni) и требует всреднем около log2(log2(N)) шагов, если упорядоченные данные имеют равномерное распределение.

Недостаток: затраты времени на дополнительные операции при внутреннем поиске. Разность между log2(log2(N)) и log2(N) становится весьма существенной при больших N, а типичные наборы данных (файлы) недостаточно случайны.

Этот алгоритм может быть достаточно успешным при поиске во внешних запоминающих устройствах.

Сортировка списков

Чтобы воспользоваться эффективными алгоритмами поиска, данные должны быть упорядочены в том или ином порядке, иначе говоря, отсортированы.

Существуют свидетельства, что первой программой для ЭВМ с хранимой программой (с архитектурой Джона Фон Неймана) была именно программа сортировки.

В зависимости от того, сортируются данные в ОЗУ или во внешнем ЗУ, сортировка бывает внетренней и внешней.

Алгоритмы сортировки делятся на группы:

· Основные

· Сортировка перестановками (обменнная);

· Сортировка выбором (отбором);

· Сортировка вставками;

· Неосновные

· Сортировка подсчетом;

· Сортировка слиянием;

· Распределяющая сортировка;

· Специальная сортировка.

Сортируемые структуры данных могут подвергаться изменениям в процессе сортировки, следовательно их элементы могут перемещаться - сортировка списка (массив); или не перемещаться, а создается таблица адресов; в таблице адресов можно ввести ключи - сортировка ключей.

Критерии выбора алгоритма:

Средняя скорость сортировки (среднее время, удельная скорость);

Скорость в лучшем и худшем случаях;

Естественность поведения;

Переставляются ли элементы с совпадающими значениями (ключами)?

Размер массива или списка, который предстоит сортировать;

Степень исходной упорядоченности сортируемых данных.

Скорость определяется количеством среавнений и перестановок. У разных алгоритмов время работы находится в экспоненциальной и логорифмической зависимости от числа элементов N.

Минимальное и максимальное время важны, если возможно частое повторение одной и той же ситуации. Часто при хорошей средней скорости алгоритмы имеют неприемлимое максимальное время выполнения.

Естественность поведения: если массив уже упорядочен, должно выполняться минимальное число операций (0). Максимальное же число операций выполняется, если массив отсортирован в обратном порядке.

Пузырьковая сортировка

Самый простой алгоритм этой группы получил название пузырьковой сортировки. Не самый удачный алгоритм. Заключается в сравнении соседних элементов и, при необходимости их перестановке. При неубывающем упорядочении элементы "выплывают" как пузырьки каждый до своего уровня.

Программа пузырьковой сортировки на языке "Паскаль"

var

str:array[0..M] of char;

procedure bubble(item:^char; n:integer);

var

a,b:integer;

t:char;

begin

for a:=1 to n-1 do

for b:=n-1 downto a do

if item[b-1]>item[b] then

begin

{Перестановка}

t:=item[b-1];

item[b-1]:=item[b];

item[b]:=t

end

end;

procedure bubble1(item:^char; n:integer);

var

a,ssign,pass:integer;

t:char;

begin

ssign:=1;

pass:=0;

while ssign<>0 do

begin

ssign:=0;

pass:=pass+1;

for a:=0 to n-pass-1 do

if item[a]>item[a+1] then

begin

t:=item[a-1];

item[a-1]:=item[a];

item[a]:=t;

ssign:=1

end

end

end;

Существуют так же текстовые модификации этой процедуры.

Описание алгоритма:

Используется два цикла. Внешний проходит N-1 раз, это гарантирует, что даже в худшем случае каждый элемент будет находиться на своем месте.

Исходнай массив d, c, a, b.

В процессе работы программы массив будет изменяться следующим образом:

d, c, a, b

a, d, c, b

a, b, d, c

a, b, c, d

Рассматриваемый вариант алгоритма всегда выполняет 1/2*(N*N-N) сравнений. Так как внешний цикл выполняется N-1 раз, а внутренний N/2.

Число перестановок зависит от степени предворительной упорядоченности массива:

В лучшем случае перестановки не выполняются (массив уже отсортирован в нужном направлении);

Всреднем выполняется 3*N*(N-1)/4 перестановок;

В худшем случае (массив отсортирован в обратном направлении) выполняется 3*N*(N-1)/2 перестановок.

Из-за наличия в формулах компонента N*N, пузырьковая сортировка относится к N-квадратичным алгоритмам. При работе с большим N, алгоритм неэффективен.

Второй вариант более длинен, но позволяет делать меньше проходов. Тип упорядоченности - по-возрастанию или по-убыванию - зависит от знака операции сравнения текущего и последующего элементов. Перестановки в массиве, аналогичном рассмотренному выше алгоритм произведет следующие:

d, c, a, b

a, d, c, b

a, b, d, c

a, b, c, d.

Сортировка вставками

На первом шаге упорядочиваются один относительно другого два первых элемента массива. Затем в упорядочивании участвуют три первых элемента (третий элемент вставляется в соответствующую позицию относительно первых двух элементов), потом - четыре и т. д., пока весь массив не будет упорядочен.

Ниже приведен пример алгоритма сортировки простыми вставками (просеиванием, или погружением)

Программа сортировки вставками на языке "Паскаль"

procedure insert(item:^char; n:integer);

var

a,b:integer; t:char;

begin

for a:=1 to n-1 do

begin

t:=item[a];

b:=a-1;

while (b>=0) and (t begin

item[b+1]:=item[b];

b:=b-1

end;

item[b+1]:=t

end

end;

Исходный массив d c a b

В отличии от предыдущих алгоритмов, число сравнений зависит от исходной упорядоченности массива. Если массив отсортирован, то N-1 сравнений, если нет, то 1/2*(N*N+N).

В исходном массиве данный алгоритм произведет следующие перестановки:

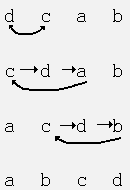
Этот алгоритм в среднем лишь немного лучше предыдущих, но обладает двумя преимуществами:

Его поведение естественно: если массив уже отсортирован в нужном порядке, алгоритм проводит минимальное количество вычислений, и максимальное, если массив отсортирован в порядке, обратном требуемому. Происходит быстрая обработка почти упорядоченных массивов.

Порядок следования одинаковых ключей не изменяется. Если список отсортирован по двум ключам, то после сортировки вставками он остается отсортированным по обоим ключам.

Недостаток:

При каждой вставке производится сдвиг массива, следовательно даже при относительно малом числе сравнений число перестановок может быть довольно значительным.

Существуют варианты: бинарные вставки, двухпутевые вставки.