Выбор или разработка математической модели и метода решения

Модель представляет собой описание объекта (предмета, процесса или явления) на каком-либо формализованном языке, составленное с целью изучения его свойств. Если речь идет о математической модели, значит она представлена на формализованном языке математики, с помощью математических понятий. Соответствие свойств модели исходному объекту характеризуется адекватностью. Процесс построения и исследования модели называется моделированием. В случае разработки программного обеспечения объектом моделирования может выступать любой элемент или элементы из предметной области, которые задействованы в процессе компьютерной обработки. Как правило, при проектировании программного обеспечения могут использоваться следующие типы моделей:

1. Приближение (параметры считаются очень большими или очень малыми). Если можно построить уравнения, описывающие исследуемую задачу, то это не значит, что их можно решить даже с помощью компьютера. Общепринятый прием в этом случае – использование приближений. Например, модель идеального газа для описания достаточно разреженных газов, где потенциальной энергией молекул можно пренебречь (т.е. считать бесконечно малой) по сравнению с их кинетической энергией.

2. Упрощение (опускаются некоторые детали). В модели отбрасываются детали, которые могут заметно и не всегда контролируемо повлиять на результат. Одни и те же уравнения могут служить моделью типа приближение или упрощение – это зависит от объекта, для изучения которого используется модель. Например, некоторые сложные нелинейные уравнения заменяются линейными, т.е. все нелинейные детали «для ясности» опускаются.

3. Эвристика (количественного подтверждения нет, но модель способствует более глубокому проникновению в суть дела). Эвристическая модель сохраняет лишь качественное подобие реальности и даёт описания объекта только «по порядку величины». Типичный пример – приближение средней длины свободного пробега в кинетической теории. Она даёт простые формулы для коэффициентов вязкости, диффузии, теплопроводности, согласующиеся с реальностью по порядку величины.

Чтобы построить математическую модель решаемой задачи, необходимо: внимательно изучить постановку задачи; выбрать или разработать математические методы, позволяющие правильно описать задачу; чётко представить на языке математики описание задачи и цели решения. Грамотное построение математической модели решения задачи – это самостоятельная научная проблема.

Любую математическую задачу можно решить двумя способами: аналитически (точно); численно (приближённо). При решении аналитическим методом исходные зависимости преобразуются так, чтобы получить математические зависимости (формулы) для точного определения результата решения. По полученным формулам можно с помощью ЭВМ получать почти точное решение. Пример такой задачи: решение квадратного уравнения. Однако большинство реальных задач нельзя решить аналитическим методом. В этом случае применяют численные методы, которые позволяют получить приближённое решение с помощью простых вычислительных действий. Пример: нахождение корня уравнения методом половинного деления (метод дихотомии). Численные методы позволяют получить приближённые решения большинства реальных задач. Разработкой численных методов занимается специальный раздел математики – вычислительная математика.

Разработка алгоритма

Алгоритм – это точный набор инструкций (команд), описывающих последовательность (порядок) действий некоторого исполнителя для достижения результата, решения некоторой задачи за конечное время. Строго говоря, понятие алгоритма необязательно относится к компьютерным программам, так, например, чётко описанный рецепт приготовления блюда также является алгоритмом, в таком случае исполнителем является человек. Однако далее в качестве исполнителя будем рассматривать ЭВМ или компьютер. В определении алгоритма под командой понимается элементарное действие, которое может выполнить исполнитель (ЭВМ), под системой команд – совокупность команд, которую может выполнить конкретный исполнитель (ЭВМ). Алгоритм должен обладать следующими важными свойствами:

1. Завершаемость (конечность) – при корректно заданных исходных данных алгоритм должен приводить к получению нужного результата за конечное число шагов.

2. Детерминированность (определённость) – в каждый момент времени следующий шаг работы однозначно определен, т.е. в алгоритме существует полная ясность каждого шага, другими словами, алгоритм должен выдавать один и тот же результат (ответ) для одних и тех же исходных данных;

3. Понятность – алгоритм для исполнителя должен включать только те команды, которые ему (исполнителю) доступны, которые входят в его систему команд.

4. Эффективность – алгоритм должен быть эффективен по времени выполнения и по емкости требуемой памяти.

5. Массовость – алгоритм должен быть применим к любым допустимым наборам исходных данных.

6. Вход – алгоритм всегда имеет некоторое (иногда равное нулю) количество входных данных, то есть величин, передаваемых ему до начала работы.

7. Выход – алгоритм всегда обязан иметь одну или несколько выходных величин.

Различают следующие простейшие виды алгоритмов:

1. Линейный – команды алгоритма выполняются шаг за шагом точно в той последовательности, в которой они представлены в алгоритме.

2. Разветвляющийся – ход исполнения команд может меняться относительно их нахождения в алгоритме. В зависимости от результата проверки условия выполняется та или иная последовательность операций, называемая ветвью.

3. Циклический – некоторые команды алгоритма многократно повторяются. В зависимости от характера повторений различают циклические алгоритмы с заданным и незаданным числом повторений (в этом случае такие алгоритмы называют итерационными, а одно повторение цикла называется итерацией).

Наиболее часто используются следующие способы описания алгоритма: словесный (вербальный), графический (в виде схем), на алгоритмическом языке или на языке программирования.

При словесном способе алгоритм задается в произвольном изложении на естественном языке. Алгоритм при таком описании строго не формализуем, многословен, допускает неоднозначности и это является большим недостатком. Однако данный способ изложения алгоритма не требует специальных знаний и может применяться конечными пользователями. Именно на этом языке, как правило, сообщается неформальная постановка задачи на этапе формализации, и он же может быть использован для представления результата первого этапа. Как правило, именно этот способ используют при объяснении какого-либо примера преподаватели, сопровождая его рисунками, схемами, графиками и т.д. Несмотря на указанные недостатки данного способа, он наиболее привычен и без него не обходится практически ни одна постановка задачи, поэтому примеров его использования можно найти множество в процессе обучения и в повседневной жизни.

Пример 1. Приведем словесное описание алгоритма, который вычисляет значение функции 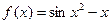на интервале 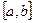с шагом h > 0. Такая задача называется задачей табулирования функции на указанном интервале с определенным шагом.

1. Начало.

2. Задать значения а, b, h.

3. Начиная со значения x, равного a, делать следующее.

4. Вычислить .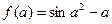

5. Вывести значения а и .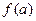

6. Увеличить значение x на шаг и вычислить .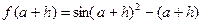

7. Вывести значения а+h и .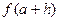

8. Увеличить значение x на шаг и вычислить .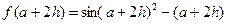

9. Вывести значения а+2h и .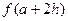

10. И так далее продолжать вычислять f, увеличивая x, до тех пор, пока х все еще меньше или равен b, т.е. последнее вычисление такое .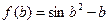

11. Вывести значения b и .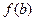

12. Конец.

При графическом описании алгоритма каждому типу действий соотносится геометрическая фигура, представленная в виде блочного символа. Действия (блоки) соединяются линиями потока. Совокупность таких связанных блоков называется блок-схемой алгоритма. Составление блок-схем регламентируется ГОСТ 19.701-90 (соответствует ISO 5807-85).

Пример 2. Построим блок-схему алгоритма для решения задачи табулирования функции (рис.1).

При записи на алгоритмическом языке каждому типу действий соотносится некоторая конструкция или команда, которую также называют оператором. Запись основных алгоритмических конструкций (операторов) в сокращенном виде на языке приближенном к естественному называют записью алгоритма на алгоритмическом языке. Если же при записи алгоритма используется строго определенный синтаксис какого-то языка программирования, то говорят о записи алгоритма на языке программирования.

Пример 3. Приведем запись алгоритма на алгоритмическом языке для решения задачи табулирования функции. Алгоритм должен соответствовать разработанной в примере 2 блок-схеме.

1. Начать работу.

2. Ввести значения a, b, h.

3. x := a (присвоить х значение а).

4. 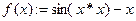(вычислить f(x)).

5. Вывести х и f(x).

6. х := x + h (увеличить х на значение h).

7. Если x > b, то перейти к п.8, иначе перейти к п.4.

8. Конец работы.