Комбинационная модель последовательностной схемы

На структурном уровне задача построения тестовой последователь­ности для заданной одиночной неисправности последовательностной схемы сводится к задаче построения тестового набора для кратной неис­правности комбинационного эквивалента последовательностной схемы.

Рассмотрим сначала комбинационный эквивалент структурного син­хронного конечного автомата (рис. 4.11, где КЧ – комбинационная часть, ЭП_i – элемент памяти, X – внешние входы, Y – внутренние состояния, Z – внешние выходы, С – синхровход).

Оборвем линии обратной связи Y и обозначим вновь образовавшиеся входы обратной связи как псевдовходы PI, а выходы элементов памяти – как псевдовыходы PO. На рис. 4.12 приведена схема, соответствующая этому случаю и названная комбинационной копией синхронного автомата. Заме­тим, что элементы памяти – это синхронные D-, T-, R-S- или J-K-триггеры.

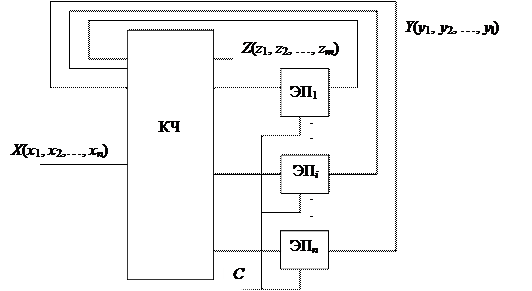
Рис. 4.11. Модель Хаффмана синхронного ЦУ

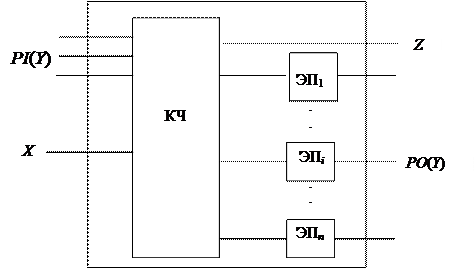Рис. 4.12. Комбинационная копия

На рис. 4.13 приведены комбинационные копии (эквиваленты) этих элементарных автоматов. Значение сигнала на входе PI представляет со­стояние q синхронного триггера в текущий момент времени, а на выходе PO – состояние Q в следующий момент времени.

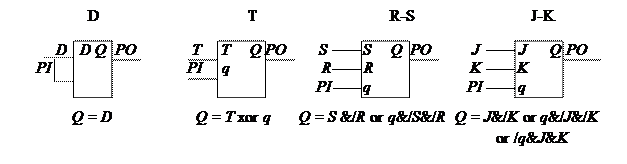
Рис. 4.13. Комбинационные эквиваленты синхронных триггеров

Комбинационная копия в условной форме представляет такт работы синхронного автомата. На рис. 4.14, а показан трехразрядный сдвиговый регистр, на рис. 4.14, б – его комбинационная копия, на рис. 4.15, а – счет­чик, а на рис. 4.15, б – его комбинационная копия.

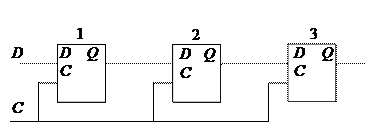
а

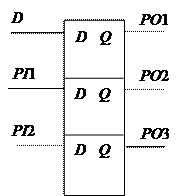
б

Рис. 4.14. Схема сдвигового регистра (а) и его комбинационная копия (б)

На рис. 4.16 приведен комбинационный эквивалент счетчика из пре­дыдущего примера, представляющий два такта его работы (копии 1 и 2) . Такую модель называют итеративной. Псевдовходы первой копии пред­ставляют начальное значение счетчика, равное 000. После первого такта (копия 1) при Е = 1 счетчик переходит в состояние 001, а после второго (копия 2) при Е = 1 – в состояние 010. Для синхронного устройства каж­дому такту соответствует только одна копия.

Рассмотрим комбинационный эквивалент структурного асинхрон­ного конечного автомата, представленного моделью Хаффмана на рис. 4.17.

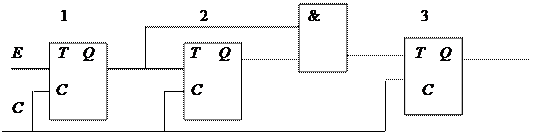
а

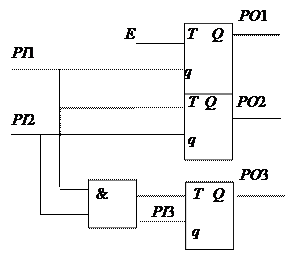
б

Рис. 4.15. Счетчик (а) и его комбинационная копия (б)

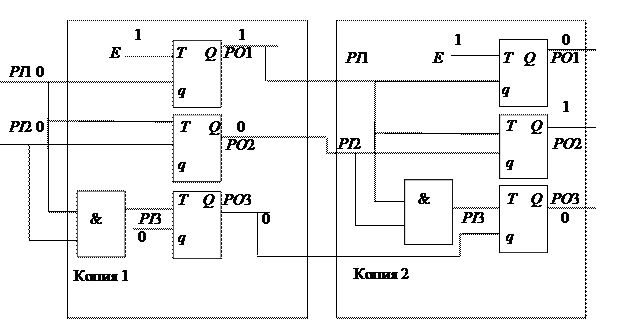
Рис. 4.16. Итеративная модель счетчика

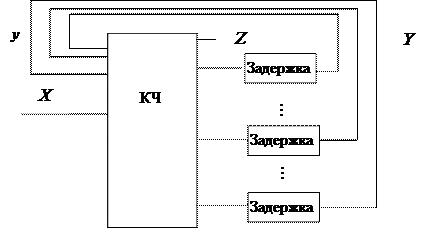
Рис. 4.17. Модель Хаффмана асинхронного ЦУ

Предполагается, что комбинационная часть (КЧ) свободна от задер­жек, а задержки сосредоточены в линиях обратной связи. В соответствии с таким представлением можно говорить об устойчивых и неустойчивых внутренних состояниях, переходы между которыми возможны только при изменении входных сигналов X. Заметим, что в синхронных автоматах пе­реход в следующее состояние инициируют тактовые импульсы. Под ус­тойчивым понимается такое состояние, при котором значения входов эле­ментов задержки равны их выходам. В асинхронном автомате переход из одного устойчивого состояния в другое (асинхронный такт работы) в об­щем случае происходит через несколько неустойчивых состояний. В ком­бинационном эквиваленте асинхронного автомата это выражается не­сколькими копиями для одного перехода, как на рис. 4.18.

Рис. 4.18. Пример комбинационного эквивалента асинхронного автомата

Копии 1 и 4 являются устойчивыми (y(1) = Y(1), y(4) = Y(4)), а 2 и 3 – неустойчивыми (y(2) ¹ Y(2), y(3) ¹ Y(3)) и отражают переход из одного ус­тойчивого состояния S_i в другое – S_j, например, как на рис. 4.19 (устойчи­вое состояние обозначено двойной окружностью).

Рис. 4.19. Фрагмент графа переходов асинхронного автомата

Построение тестовой последовательности по комбинационной модели последовательностной схемы

Очевидно, что для комбинационного эквивалента последовательно­стной схемы может быть применен метод существенного пути для по­строения тестовой последовательности с определенными ограничениями и условиями:

1. Одиночная неисправность представляется n-кратной, где n – число копий.

2. Точками наблюдения являются внешние выходы последней копии.

3. Начальное состояние устройства предполагается неизвестным, по­этому обязательным ограничением является сохранение на псевдовходах первой копии неопределенных значений.

Длина проверяющей последовательности для синхронных устройств равна числу копий, а для асинхронных она не больше числа копий и не может быть известна заранее. Построение проверяющей последовательно­сти начинается с попытки построить последовательность длины 1. Если этого не удается сделать, то принимают длину 2 и так далее, пока не дос­тигнут заранее заданного порога. Это означает, что процедура построения теста для последовательностных устройств не является алгоритмом (нет гарантии построения тестовой последовательности). При числе копий больше двух следует рассматривать варианты образования существенного пути как от неисправного узла одной копии, так и от неисправных узлов других копий. В случае асинхронных устройств смена входного набора должна происходить только в устойчивых состояниях, для которых PI = = PO.

Рассмотрим пример построения тестовой последовательности для схемы (рис. 4.20) асинхронного автомата и неисправности С0 на линии 1. Обрыв выделенных линий обратной связи приводит к комбинационной копии (рис. 4.21).

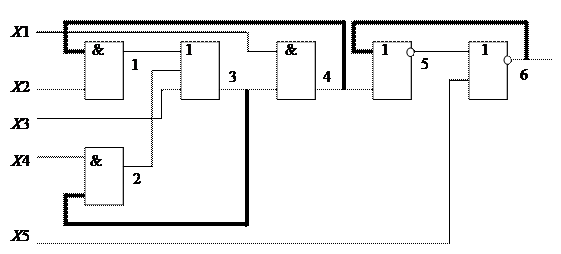
Рис. 4.20. Пример асинхронной последовательностной схемы

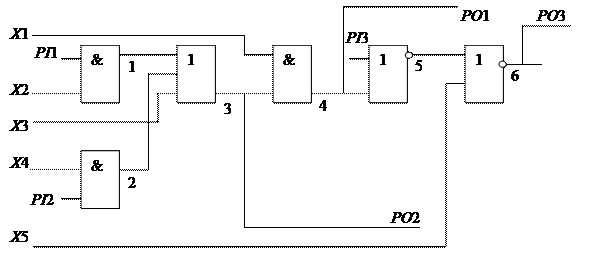
Рис. 4.21. Комбинационная копия схемы из примера на рис. 4.20

Построение последовательности длины 1. Зададим условие про­явления неисправности. Единственный вариант требует установки 1 на псевдовходе PI1, что противоречит ограничению 3:

X1

PI3

PI1

X2

X3

X4

PI2

X5

3(PO2)

4(PO1)

6(PO3)

x

x

1/x

x

x

x

x

1/0

x

x

x

x

x

копия 1

Построение последовательности длины 2. Зададим условие про­явления неисправности. Единственный вариант требует установки 1 на псевдовходе PI1 и 1 на внешнем входе Х2 в копии 2. Значение PI1 = 1 мо­жет быть однозначно доопределено в первой копии: Х1 = 1, 3 = *1/x. Зна­чение 3 = *1/x в первой копии однозначно доопределить нельзя, поэтому оно отмечается * для последующего доопределения. Импликация во вто­рой копии значения 1/0 на линии 1 приводит к 3 = 1/x:

X1

PI3

PI1

X2

X3

X4

PI2

X5

3(PO2)

4(PO1)

6(PO3)

x

x

x

x

x

x

x

x

x

*1/x

x

x

x

копия 1

x

x

1/x

x

x

x

x

1/0

x/x

1/x

x/0

x

x

копия 2

Выбираем путь от места неисправности до выхода схемы: 1-3-4-5-6. Выбираем условия активизации первого элемента пути: Х3 = 0, 2 = х/0. Однозначное доопределение 2 = х/*0 невозможно (отмечаем *). Имплика­ция приводит к 3 = 1/0 и 4 = х/0:

X1

PI3

PI1

X2

X3

X4

PI2

X5

3(PO2)

4(PO1)

6(PO3)

x

x

x

x

x

x

x

x

*1/x

x

x

x

x

копия 1

x

x

1/x

x

x

x

1/0

x/*0

1/0

x/0

x

x

копия 2

Копия 2 неустойчива, так как PI1 ¹ PO1 и PI2 ¹ PO2; следовательно, вводим копию 3 с Х2 = 1, Х3 = 0, PI1 = x/0, PI2 = 1/0. Имплицируем эти значения в копии 3:

X1

PI3

PI1

X2

X3

X4

PI2

X5

3(PO2)

4(PO1)

6(PO3)

x

x

x

x

x

x

x

x

x

*1/x

x

x

x

копия 1

x

x

1/x

x

x

x

1/0

x/*0

1/0

x/0

x

x

копия 2

x

x

x/0

x

1/0

x

1/0

x/0

1/0

x/0

x

x

копия 3

Выбираем условие активизации следующего элемента пути в ко­пии 3: Х1 = 0 и имплицируем это значение:

X1

PI3

PI1

X2

X3

X4

PI2

X5

3(PO2)

4(PO1)

6(PO3)

x

x

x

x

x

x

x

x

x

*1/x

x

x

x

копия 1

x

x

1/x

x

x

x

1/0

x/*0

1/0

x/0

x

x

копия 2

x

x/0

x

1/0

x

1/0

x/0

1/0

1/0

0/x

x

копия 3

Копия 3 неустойчива, так как PI1 ¹ PO1, следовательно, вводим ко­пию 4 с Х1 = 1, Х2 = 1, Х3 = 0, PI1 = 1/0. Имплицируем эти значения в ко­пии 4:

X1

PI3

PI1

X2

X3

X4

PI2

X5

3(PO2)

4(PO1)

6(PO3)

x

x

x

x

x

x

x

x

x

*1/x

x

x

x

копия 1

x

x

1/x

x

x

x

1/0

x/*0

1/0

x/0

x

x

копия 2

x

x/0

x

1/0

x

1/0

x/0

1/0

1/0

0/x

x

копия 3

x

1/0

x

x

1/0

x/0

1/0

1/0

0/x

x

копия 4

Выбираем условие активизации предпоследнего элемента пути в ко­пии 4: PI3 = x/*0 и имплицируем это значение:

X1

PI3

PI1

X2

X3

X4

PI2

X5

3(PO2)

4(PO1)

6(PO3)

x

x

x

x

x

x

x

x

x

*1/x

x

x

x

копия 1

x

x

1/x

x

x

x

1/0

x/*0

1/0

x/0

x

x

копия 2

x

x/0

x

x

x

1/0

x/0

1/0

1/0

0/x

x

копия 3

x/*0

x/0

x

x

x

1/0

x/0

1/0

1/0

0/1

x/0

копия 4

Выбираем условие активизации последнего элемента пути в копии 4: X5 = 0 и имплицируем это значение:

X1

PI3

PI1

X2

X3

X4

PI2

X5

3(PO2)

4(PO1)

6(PO3)

x

x

x

x

x

x

x

x

x

*1/x

x

x

x

копия 1

x

x

1/x

x

x

x

1/0

x/*0

1/0

x/0

x

x

копия 2

x

x/0

x

x

x

1/0

x/0

1/0

1/0

0/x

x

копия 3

x/*0

x/0

x

x

1/0

x/0

1/0

1/0

0/1

1/0

копия 4

Копия 4 неустойчива, так как PI3 ¹ PO3, следовательно, вводим ко­пию 5 с Х1 = 1, Х2 = 1, Х3 = 0, X5 = 0, PI3 = 1/0. Имплицируем эти значения в копии 5. Путь активизирован:

X1

PI3

PI1

X2

X3

X4

PI2

X5

3(PO2)

4(PO1)

6(PO3)

x

x

x

x

x

x

x

x

x

*1/x

x

x

x

копия 1

x

x

*1/x

x

x

x

1/0

x/*0

1/0

x/0

x

x

копия 2

x

x/0

x

x

x

1/0

x/0

1/0

1/0

0/x

x

копия 3

x/*0

x/0

x

x

1/0

x/0

1/0

1/0

0/1

1/0

копия 4

1/0

x/0

x

x

1/0

x/0

1/0

1/0

0/1

1/0

копия 5

Выполним доопределение для сигналов, отмеченных *. Значение PI3 в копии 4 равно значению PO в копии 3, выбираем вариант доопределения этого сигнала – X5 = 1 в копии 3, имплицируем полученное значение:

X1

PI3

PI1

X2

X3

X4

PI2

X5

3(PO2)

4(PO1)

6(PO3)

x

x

x

x

x

x

x

x

x

*1/x

x

x

x

копия 1

x

x

1/x

x

x

x

1/0

x/*0

1/0

x/0

x

x

копия 2

x

x/0

x

x

1/0

x/0

1/0

1/0

0/x

копия 3

x/0

x

x

1/0

x/0

1/0

1/0

0/1

1/0

копия 4

1/0

x/0

x

x

1/0

x/0

1/0

1/0

0/1

1/0

копия 5

Доопределим значение сигнала 2 в копии 2. Выбираем вариант Х4 = 0 и имплицируем это значение:

X1

PI3

PI1

X2

X3

X4

PI2

X5

3(PO2)

4(PO1)

6(PO3)

x

x

x

x

x

x

x

x

x

*1/x

x

x

x

копия 1

x

x

1/x

x

x

1/0

1/0

x/0

x

x

копия 2

x

x/0

x

x

1/0

x/0

1/0

1/0

0/x

копия 3

x/0

x

x

1/0

x/0

1/0

1/0

0/1

1/0

копия 4

1/0

x/0

x

x

1/0

x/0

1/0

1/0

0/1

1/0

копия 5

Доопределим значение сигнала 3 в копии 1. Выбираем вариант Х3 = 1 и завершаем построение теста, так как больше нет отмеченных сигналов:

X1

PI3

PI1

X2

X3

X4

PI2

X5

3(PO2)

4(PO1)

6(PO3)

x

x

x

x

x

x

x

x

x

x

x

копия 1

x

x

1/x

x

x

1/0

1/0

x/0

x

x

копия 2

x

x/0

x

x

1/0

x/0

1/0

1/0

0/x

копия 3

x/0

x

x

1/0

x/0

1/0

1/0

0/1

1/0

копия 4

1/0

x/0

x

x

1/0

x/0

1/0

1/0

0/1

1/0

копия 5

Выделим входные значения:

Х1	Х2	Х3	Х4	Х5
	x		x	x	копия 1
x				x	копия 2
			x		копия 3
			x		копия 4
			x		копия 5

Удалим одинаковые соседние копии:

Х1	Х2	Х3	Х4	Х5
	x		x	x	копия 1
x				x	копия 2
			x		копия 3
			x		копия 4

Доопределим неопределенные значения из условия минимального от­личия соседних наборов:

Х1	Х2	Х3	Х4	Х5
					копия 1
					копия 2
					копия 3
					копия 4

Удалим одну из одинаковых соседних копий (копия 3) и заново пе­ренумеруем их:

Х1	Х2	Х3	Х4	Х5
					копия 1
					копия 2
					копия 3

Окончательный результат:

Х1	Х2	Х3	Х4	Х5
					1/0						Т1
					1/0		1/0	1/0	0/1		Т2
					1/0		1/0	1/0	0/1	1/0	Т3

Построение тестов выполняется по модели с нулевыми задержками элементов. Однотактные задержки сосредоточены в линиях обратной связи, и каждая копия соответствует такой задержке. Для определения од­нозначности поведения устройства в исправном и неисправном случае не­обходимо выполнять синхронное троичное моделирование.

Сценарий построения тестовой последовательности включает в себя:

1. Построение тестовой последовательности для очередной неис­правности из списка необнаруженных.

2. Моделирование неисправностей из списка необнаруженных на по­лученной входной последовательности.

3. Сокращение списка неисправностей на величину обнаруженных неисправностей и т.д.