Теоретические сведения. Пусть имеется урна с десятью шарами, из которых 6 белых и 4 черных

Пусть имеется урна с десятью шарами, из которых 6 белых и 4 черных. Тогда возможны следующие события:

А – вынуть белый шар из урны

В – вынуть черный шар из урны

Событие А состоит из событий А₁,А₂, А₃, А₄, А₅, А₆. Событие В состоит из событий В₁, В₂, В₃, В₄. Тогда процент белых шаров в урне определиться как отношение 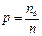, а процент черных шаров .

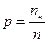Определение:Вероятностью события А наз. число, равное отношению числа исходов m благоприятствующих наступлению события А к общему числу всех элементарных исходов n.

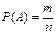- формула классического способа подсчета вероятности

Вероятность случайного события есть число, заключенное между нулем и единицей

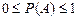
Определение:Перестановки– это комбинации, составленные из всех п элементов данного множества и отличающиеся только порядком их расположения. Число всех возможных перестановок

Р_п = п!

Определение:Размещения – комбинации из т элементов множества, содержащего п различных элементов, отличающиеся либо составом элементов, либо их порядком. Число всех возможных размещений

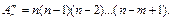
Определение:Сочетания – неупорядоченные наборы из т элементов множества, содержащего п различных элементов (то есть наборы, отличающиеся только составом элементов). Число сочетаний

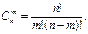
Пример 1. В отборочных соревнованиях принимают участие 10 человек, из которых в финал выходят трое. Сколько может быть различных троек финалистов?

Решение. В отличие от предыдущего примера, здесь не важен порядок финалистов, следовательно, ищем число сочетаний из 10 по 3:

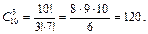
Ответ: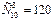

Пример 2. В урне 10 шаров: 6белых и 4черных. Из нее вынимают два шара. Какова вероятность того что: а) 2белых; б) 2черных; в) 1белый,1черный

Решение:

а) пусть А – вынуты 2белых шара. Найдем общее число всех элементарных исходов n.

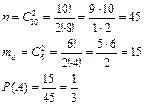
б) пусть В – вынуты 2 черных шара

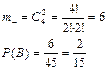
в)пусть С – вынут 1белый и 1черный шар

n=45

m_c=6*4=24

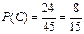
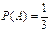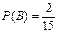Ответ: а) б) в)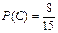

Задание для самостоятельной работы:

Подобрать три задачи на использование формул комбинаторики, формулы классического способа подсчета вероятностей. Оформить согласно требований.

Рекомендуемая литература: 2;3;4.