Построение пути минимальной длины

Пусть задано множество ячеек дискретного поля, на котором построено некоторое число проводников. Требуется построить новый проводник между точками A и B так, чтобы он не пересекал ранее построенные проводники и имел минимально возможную длину (рис.7.8).

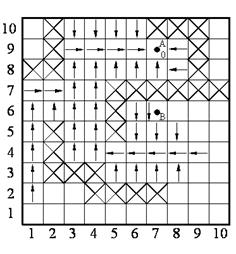
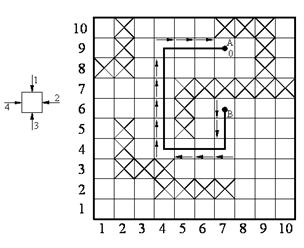
Рис.7.8. Рис.7.9.

Распространение волны начинаем из источника – точки A, вес которой положим равным нулю. Строим расширяющийся фронт волны влияний, распространяющийся на все соседние свободные с этой точкой ячейки. Каждая ячейка фронта генерирует следующий фронт волны, который занимает все соседние свободные с первым фронтом ячейки и т. д. Вес ячейки k-го фронта считается равным весу соседней ячейки (k – 1)-го фронта плюс единица, т. е. 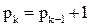. Процесс распространения волны продолжаем до тех пор, пока не достигнем ячейки с точкой B (целью). Процесс поиска пути из A в B в соответствии с рассмотренным алгоритмом для данного варианта трассировки показан на рис.7.8. В каждой ячейке указаны приписанные ей на этапе распространения волны путевые координаты и веса. Ячейка B достигается при построении 16-го фронта волны.

Проведение пути начинаем с ячейки B (цели). Просматриваем окрестность точки цели (приемника) и находим ячейку, которая в наиболее приоритетном направлении имеет вес на единицу меньше. Перемещаемся в эту ячейку и отмечаем след перехода. Процесс продолжаем до тех пор, пока след не приведет в точку A. На рис.7.9 показан вновь проведенный путь. Из него видно, что построенный проводник действительно является кратчайшим между точками A и B, причем его относительная длина равна весу, присвоенного ячейке B.

В данном случае путевая координата несет избыточную информацию. Действительно, при проведении пути использовались только данные о весе просматриваемой ячейки, а приоритет его проведения учитывался последова-тельностью просмотра этих ячеек.

Достоинства волнового алгоритма: возможность нахождения пути мини-мальной длины в любом лабиринте, если существует хотя бы один путь в нем.

Недостатками волнового алгоритма Ли являются малое быстродействие и большой объем оперативной памяти ЭВМ, необходимый для хранения инфор-мации о текущем состоянии всех ячеек коммутационного поля.

Алгоритм Акерса

Наиболее экономичный способ кодирования состояний ячеек коммутаци-онного поля предложен Акерсом [1 – 4]. При распространении волны ячейки поля получают отметки в соответствии с базовой последовательностью 1, 1, 2, 2, 1, 1, 2, 2, … . Данная последовательность характерна тем, что в ней любой член имеет разных соседей слева и справа. Вначале все незанятые ячейки, соседние с ячейкой-источником, помечаются 1, затем все ячейки фронта 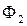помечаются так же 1. Далее отметка 2 присваивается ячейкам фронта и т. д. (рис.7.10).

Для построения пути в общем случае необходимо найти требуемую под-по-следовательность отметок базовой последовательности. Это легко может быть сделано по отметке ячейки-цели и отметке соседней с ней ячейки. В нашем случае цель достигнута первой 1, поэтому надо искать ячейку с отметкой 2. Их две: внизу и слева. Воспользуемся приоритетом. Вначале просматриваем ячейку снизу от цели. Поскольку ее вес равен 2, путь строим в нее. В ней вновь анализируем соседние ячейки в порядке приоритета. Ищем ячейку с весом 2. Это опять нижняя ячейка. Далее надо аналогично искать ячейку с весом 1.

Вариант соединения контактов A и B при этом заданном приоритете дан на рис.7.10.

В методе Акерса ячейка поля может находиться в следующих состояниях: пустая, занятая, иметь отметку 1 или 2. Таким образом, на каждую ячейку поля достаточно всего два двоичных разряда памяти.

Лучевой алгоритм

Основная идея алгоритма, предложенного Л. Б. Абрайтисом [1 – 4], заклю-чается в исследовании поля для определения пути между ячейками A и B по некоторым заранее заданным направлениям, подобным лучам. Это позволяет сократить число просматриваемых алгоритмом ячеек, а, следовательно, и время на анализ и кодировку их состояний, однако снижает вероятность нахождения пути сложной конфигурации и усложняет учет конструктивных требований к технологии печатной платы.

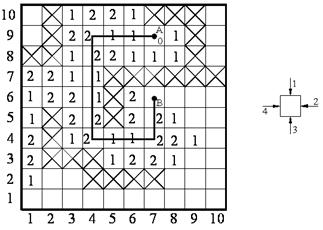
Рис.7.10.

Работа алгоритма заключается в следующем. Задается число лучей, распро-страняемых из ячейки A и B, а также порядок присвоения путевых координат. Обычно число лучей для каждой из ячеек (источников) принимают одинаковым (часто равным двум). Луч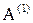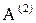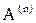и , , …, и 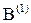, , 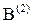…, 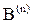считаются одноименными, если они распространяются из одноименных источников A или B. Луч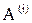и и 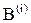являются разноименными по отношению друг к другу. Распространение лучей происходит одновременно из обоих источников до встречи двух разноименных лучей в некоторой точке C.

Путь проводится из ячейки C, в которой встретились лучи по путевым координатам, и проходит через ячейки, по которым распространялись лучи.

При распространении луча может возникнуть ситуация, когда две соседние ячейки будут заняты. В этом случае луч считается заблокированным и его рас-пространение прекращается.

Рассмотрим работу лучевого алгоритма на примере (рис.7.11).

Для источников A и B взято по два луча с взаимно противоположными направлениями. Поскольку разности координат 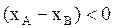и 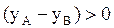, то для луча 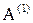допустимое направление движения вначале вниз, а в случае преграды – вправо; для луча 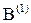– вверх, влево; для 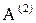– вправо, вниз; для 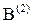– влево, вверх. Если ячейка B будет расположена не справа от A, а слева, то путевые координаты вправо и влево надо поменять местами.

На первом шаге алгоритма просматриваются ячейки с координатами (3,8), (9,3), (4,9) и (8,2). Поскольку эти ячейки оказались свободными, в них ставятся путевые координаты, которые указывают назад, т.е. на те ячейки, из которых на

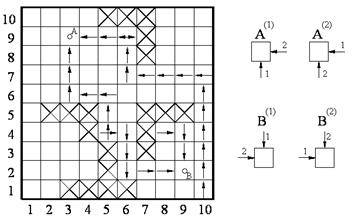
Рис.7.11.

этом шаге поступил луч. На третьем шаге луч 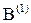сверху оказывается забло-кированным, поэтому он меняет направление «вверх» на направление «влево» – просматривается ячейка с координатами (8,4). На четвертом шаге луч 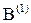оказывается заблокированным, а луч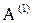и и 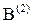встретились в ячейке C с координатами (5,4). Луч 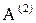, пройдя через все поле, оказывается заблоки-рованным в ячейке с координатами (10,1).

Путь строится из ячейки C по путевым координатам в направлении ячеек A и B. Если бы ячейка (7,2) была занята, то луч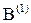и и 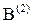оказались бы заблокированными, и решение найдено не было, хотя путь из A в B провести можно.

Достоинства алгоритма: получение соединений минимальной длины и высокое быстродействие.

Недостаток: не всегда находит решение, хотя оно может существовать, при трассировке двухслойных плат с ортогональной коммутацией с помощью лучевого алгоритма удается построить до 70% трасс, а остальные проводят, используя волновой алгоритм или вручную.

Поэтому лучевой алгоритм целесообразно применять для трассировки плат с небольшой степенью заполнения ячеек или в начальной стадии трассировки совместно с волновым алгоритмом. В этом случае удается значительно экономить время.

ДОМАШНЕЕ ЗАДАНИЕ

2.1. Ознакомиться с методами решения задачи трассировки печатных соединений.

2.2. Изучить волновой алгоритм Ли, Акерса и лучевой Абрайтиса.

2.3. Подготовить данные к эксперименту.

2.4. Выполнить трассировку печатных соединений «вручную» волновым и лучевым алгоритмами.

ЗАДАНИЕ К ЛАБОРАТОРНОЙ РАБОТЕ

3.1. Порядок работы с программой «PSTRAS»

Алгоритмы трассировки печатных соединений схем реализованы в пакете учебной САПР PSAPRна ПЭВМ программой “PSTRAS”. Программа позволяет трассировать печатные соединения алгоритмами:

- волновым Ли в Евклидовой (по восьми) и ортогональной (по четырем направлениям) метриках;

- алгоритмом Акерса в ортогональной метрике;

- лучевым алгоритмом Абрайтиса в Евклидовой и ортогональной метриках.

Для запуска программы «PSTRAS» установить курсор на окно «Трассировка печатных соединений» (оно будет в зелёной рамке) и нажать Enter. Появится рабочее поле графического редактора «PSTRAS» (рис.7.12).

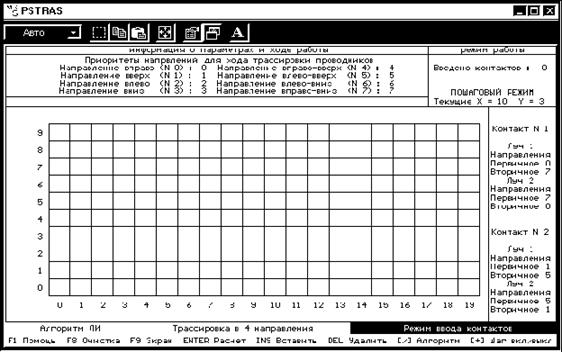Рис.7.12.

В верхней части экрана размещены слева направо зоны установки приоритетных направлений распространения лучей и рабочего режима.

В центральной части разбитое на квадратные ячейки рабочее поле.

Справа зона установки направлений распространения лучей.

В нижней части экрана приведены зоны выбора алгоритма, вида трассировки и режимов ввода контактов и препятствий (проводников).

При вызове программы на экране появится рабочее поле, разбитое на квадратные ячейки. В ячейке с координатами (0, 0) находится курсор в виде желтого квадрата. Перемещая с помощью курсора этот квадрат по полю, отдельные контакты цепи вводятся в нужных местах нажатием клавиши [Insert]. Все параметры программы устанавливаются указанием на них курсором манипулятора и щелчком левой кнопки.

Кроме этого управление возможно с клавиатуры. Клавишей [-] переключа-ется программа в режим ввода препятствий, которые задаются также нажатием клавиши [Insert]. На экране такие ячейки поля выделяются красным цветом.

Для удаления контакта или препятствия необходимо установить на них курсор и нажать клавишу [Delete].

Перед трассировкой соединений с помощью клавиши [/] необходимо вы-брать один из алгоритмов (волновой Ли, Акерса или лучевой). Клавишей [*] задать количество направлений распространения числовой волны (4 или 8).

Информация о выбранном алгоритме, направлениях, режиме ввода (кон-тактов либо препятствий) выводится в нижней части экрана.

Режим работы программы (автоматический или пошаговый) задается клавишей [+] и высвечивается в правом верхнем углу экрана. Приоритеты для каждого из восьми направлений трассировки задаются одновременным нажатием клавиши [Alt] и одной из клавиш цифр от 0 до 7. При этом наиболее предпочтительным является нулевое направление, а затем в порядке возрастания чисел. Информация о заданных приоритетах также выводится в правой части экрана.

Трассировка по алгоритму Акерса выполняется в пошаговом режиме. В случае зацикливания программ необходимо одновременно нажать клавиши [Alt] и [Pause]. Каждый последующий шаг в этом режиме выполняется клавишей [Enter].

Удаление выполняется клавишей [Esc].

В процессе работы с программами атрибуты могут изменяться манипулято-ром типа «мышь». Для этого вначале указывается один из изменяемых пара-метров (режим работы программы, изменяемый приоритет направления или одна из команд командной строки в нижней части экрана), а затем нажимается левая клавиша манипулятора.

При работе лучевого алгоритма направления распространения лучей устанавливаются клавишами [0] – [7]. При этом информация о направлении распространения лучей отображена в правой части экрана. Изменять данную информацию можно и манипулятором типа «мышь».

Коды направлений распространения луча, в данном случае следующие: 0 – означает, что луч будет двигаться вправо; 1 – вверх; 2 – влево; 3 – вниз; 4 – вправо-вверх; 5 – влево-вверх; 6 – влево-вниз; 7 – вправо-вниз.

Пример

Для работы программы необходимо выбрать алгоритм: в режиме ввода контактов установить два контакта, нажатием клавиши Insert. Затем переклю-читься на режим ввода препятствий и ввести проводники (рис.7.13).

Для получения соединения в пошаговом режиме распространить нажатием на клавишу Enter цифровую волну до момента достижения ячейки цели (рис.7.14). После этого над рабочим полем появляется трансляция: «Волна достигла цели, нажмите любую клавишу для построения трассы».

Рис.7.13.

После этого нажатием клавиши Enter построить трассу (рис.7.15).

Теоретическая часть

3.1.1. Получить у преподавателя технические условия на проектирование печатного монтажа.

3.1.2. Для заданных вариантов электрических цепей и монтажного про-странства составить необходимые математические модели.

3.1.3. По алгоритмам Ли, Акерса и лучевому «вручную» построить соединения между заданными контактами.

Рис.7.14.

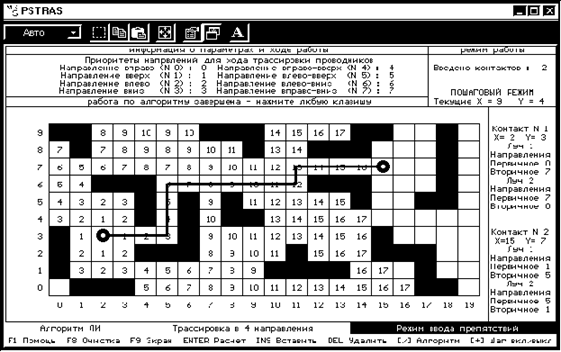Рис.7.15.

Экспериментальная часть

3.2.1. Выбрать волновой алгоритм Ли, задать контакты одной цепи и ранее построенные проводники:

-задать четыре направления трассировки и построить по этому алгоритму соединения (трассы).

- задать восемь направлений трассировки (под любыми углами) и вновь построить по алгоритму трассы.

3.2.2. Выбрать алгоритм Акерса и для тех же контактов цепи и проводников просчитать по программе варианты построения соединений.

3.2.3. Выбрать лучевой алгоритм Абрайтиса и для ранее введенных контактов цепи и проводников просчитать по программе варианты построения соединений.

3.2.4. Результаты расчетов записать (вывести на печать) и оформить в виде эскизов соединения выводов электрических цепей.

3.2.5. Результаты трассировки оценить по всем критериям;

сравнить результаты ручного и машинного расчётов.

3.2.6. Оценить эффективность исследуемых алгоритмов трассировки с точки зрения требований к математическому обеспечению САПР.

СОДЕРЖАНИЕ ОТЧЕТА

4.1. Цель работы.

4.2. Сведения из теории. Задача трассировки печатных соединений и её математическая формулировка.

4.3. Графическое изображение на плоскости в декартовой системе координат контактов, множества цепей, подлежащих соединению.

4.4. Математические модели соединяемых контактов, необходимые для работы алгоритмов.

4.5. Результаты трассировки соединений «вручную» и на ЭВМ.

4.6. Эскизы результатов проектирования проводного монтажа.

4.7. Выводы.

КОНТРОЛЬНЫЕ ВОПРОСЫ

5.1. Сформулируйте цели задачи трассировки печатных соединений.

5.2. Как математически формулируется задача трассировки печатных соединений?

5.3. Назовите основные алгоритмы трассировки печатных соединений и в чем их основное различие?

5.4. Каким образом можно оценить качество печатного монтажа?

5.5. Перечислите последовательность действий волнового алгоритма Ли и продемонстрируйте его работу на примере.

5.6. Перечислите последовательность действий лучевого алгоритма и продемонстрируйте его работу на примере.

5.7. Перечислите последовательность действий алгоритма Акерса и проде-монстрируйте его работу на примере.

5.8. Назовите достоинства и недостатки волнового, лучевого и алгоритма Акерса.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Селютин В. А. Машинное конструирование электронных устройств. – М.: Сов. радио, 1977. – 384 с.

2. Деньдобренко Б. Н., Малика А. С. Автоматизация конструирования РЭА. – М.: Высшая школа. 1980. – 384 с.

3. Морозов К. К., Одиноков В. Г., Курейчик В. М. Автоматизированное проектирование конструкций РЭА: Учеб. пособие для вузов. – М.: Радио и связь, 1983. – 280 с.

4. Курейчик В. М. Математическое обеспечение конструкторского и техно-логического проектирования с применением САПР: Учеб. для вузов. – М.: Радио и связь, 1990. – 352 с.

5. Теория и методы автоматизации проектирования вычислительных систем / Под ред. М. Брейера. – М.: Мир, 1977. – 283 с.

6. Савельев А. Я., Овчинников В. А. Конструирование ЭВМ и систем. – М.: Высшая школа, 1989. – 248 с.

7. Кристофидес Н. Теория графов: Автоматический подход: Пер. с англ. – М.: Мир, 1978. – 432 с.

8. Кофман А. Введение в прикладную комбинаторику: Пер. с фр. – М.: Наука, 1975. – 480 с.

9. Алипов Н. В. Задачник по автоматизации конструкторского проектирова-ния РЭА и ЭВА. – М.: Высшая школа, 1986. – 160 с.

10. Мудров В. И. Задача о коммивояжере. Новое в жизни, науке, технике. Серия Математика, Кибернетика. – М. Знание, 1969. – 62 с.

Содержание

ЛАБОРАТОРНАЯ РАБОТА №5

Исследование эффективности алгоритмов трассировки проводных соединений . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3

1. Алгоритмы трассировки проводов . . . . . . . . . . . . . . . . . . . . . . 3

2. Домашнее задание . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .15

3. Задания к лабораторной работе . . . . . . . . . . . . . . . . . . . . . . . 15

4. Содержание отчета . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18

5. Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19

ЛАБОРАТОРНАЯ РАБОТА №6

Исследование эффективности алгоритмов трассировки проводов

в жгуты . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .20

1. Задача о максимальном потоке . . . . . . . . . . . . . . . . . . . . . . . 20

2. Домашнее задание . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28

3. Задания к лабораторной работе . . . . . . . . . . . . . . . . . . . . . . . 29

4. Содержание отчета . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30

5. Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31

ЛАБОРАТОРНАЯ РАБОТА №7

Исследование эффективности алгоритмов трассировки печатных и пленочных соединений . . . . . . . . . . . . . . . . . . . . . . . . . . . 32

1. Сведения из теории . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .32

2. Домашнее задание . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .39

3. Задания к лабораторной работе . . . . . . . . . . . . . . . . . . . . . . . 40

4. Содержание отчета . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44

5. Контрольные вопросы . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44

Библиографический список . . . . . . . . . . . . . . . . . . . . . . . . . . 45

Учебное издание

МАКТАС Михаил Яковлевич

Исследование алгоритмов трассировки

проводных и печатных соединений РЭС

Сборник лабораторных работ

Редактор Н.А.Евдокимова

Подписано к печати 20.02.2003 Формат 60 х 84 / 16

Бумага писчая. Печать трафаретная. Усл. печ. л. 2,40.

Уч. изд. л. 2,00. Тираж 150 экз. Заказ

Ульяновский государственный технический университет

432027. г. Ульяновск, ул. Сев. Венец, д.32.

Типография УлГТУ, 432027. г. Ульяновск, ул. Сев. Венец, д.32.