Встраивание путем модификации отношения между значениями коэффициентов в пределах одного блока 4 страница

(5.47)

Модулированное сообщение Е(х,у), полученное при этом, попиксельно суммируется с изображением-контейнером С(х,у) в качестве которого используется полутоновое изображение размером . Результатом является стеганоизображение при

Чтобы сделать невозможным искажение уже встроенного бита сообщения, базисные функции должны быть ортогональными:

(5.48)

где — количество значащих пикселей в базисной функции; — средняя мощность, приходящаяся на пиксель ; -дельта-символ Кронекера.

В идеальном случае, все базисные функции должны быть некоррелированными с изображением-контейнером С, то есть должны быть ортогональными к нему: . Однако на практике тяжело найти контейнер, который был бы полностью ортогональным ко всем базисным функциям . В таком случае должна быть введена величина погрешности , которая учитывается увеличением мощности .

Для эффективного скрытия информации необходимо значительное количество базисных функций, ортогональных к типичным изображениям. Кодирование же изображении выдвигает противоположное требование: идеальным считается небольшое количество базисных функций, которые приблизительно перекрывает всю область изображения. Эти требования вступают в конфликт, когда изображение, содержащее скрытую информацию, подвергается компрессии: идеальная схема компрессии не способна полностью отобразить базисы, которые использовались для скрытия.

Базисные функции могут быть организованы и сравнимы в соответствии с такими свойствами как полная мощность, степень пространственного расширения (или локализации), а также степень пространственного частотного расширения (или локализации) [88].

В случае РСПП модулирующая функция состоит из постоянного коэффициента усиления G (целое число), умноженного на псевдослучайный блок (массив) базисных функций , значений ±1. Каждый массив имеет индивидуальное расположение в массиве. Кроме того, массивы являются непересекающимися (то есть заведомо ортогональными друг к другу) и перекрывают -массив без промежутков.

Также будем считать, что все базисные функции имеют одинаковое количество значащих элементов . В этом случае полную мощность можно записать следующим образом:

(5.49)

На этапе извлечения данных нет необходимости владеть информацией о первичном контейнере С. Операция декодирования заключается в восстановлении скрытого сообщения путем проецирования полученного стеганоизображения S* на все базисные функции :

.

Значения могут быть легко восстановлены с помощью знаковой функции:

(5.50)

Если , то скрытая информация была утрачена. При малых значениях средней мощности G² возрастает вероятность извлечения ошибочного значения бита информации, однако контейнер при этом искажается в меньшей степени.

Основное преимущество стеганографических методов, основанных на расширении спектра — сравнительно высокая стойкость к различного рода атакам на изображение, поскольку скрываемая информация распределена в широкой полосе частот и ее трудно удалить без полного разрушения контейнера. Искажения стеганоизображения увеличивают значение 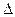, однако до тех пор, пока выполняется условие , скрытое сообщение не пострадает.

Приведем пример реализации метода стеганографического скрытия с помощью расширения спектра в программе MathCAD.

Шаг 1

Импортируем изображение-контейнер:

С := READBMP("C. bmp");

X := rows(C); X=128;

Y:=cols(C); Y:=128.

Шаг 2

Формируем массив ортогональных базисных функций, который должен иметь размерность сигнала-контейнера и представлять собой сумму всех базисных неперекрывающихся функций .

Очевидно, что для получения ортогональных базисных функций достаточно провести деление массива на непересекающиеся сегменты, каждый из которых поместить в массив нулевых элементов размерностью по соответствующим координатам.

Генерирование массива осуществляется программным модулем (М.89). При этом +1 и -1 чередуются в шахматном порядке. Конечно, при создании более надежной стеганосистемы необходимо выбрать более сложный алгоритм формирования массива ортогональных базисных функций.

Шаг 2

Пусть общее количество базисных функций . Размерность значащего подмассива отдельной базисной функции (размерность выделяемого сегмента) определим, исходя из размерности массива и общего количества базисных функций

Формирование массива базисных функций осуществим путем выделения соответствующего базисной функции значащего подмассива из общего массива и последующего его встраивания на соответствующие позиции нулевого массива размерностью с помощью функции . Указанные операции осуществляет программный модуль (М.90)

Для упрощения, нулевой массив формируется умножением на 0 массива . Результат присваивается псевдослучайному элементу массива . Для генерирования ПСП используется программный модуль (M.57) при следующих исходных значениях:

• примитивный полином 8-й степени , например, следующего вида; , что означает

;

• значение начального состояния регистра s — произвольное целое число из диапазона возможных значений

Графическое отображение массива и некоторых массивов базисных функций приведены на рис. 5.53.

Рис. 5.53. Графическая интерпретация массивов ортогональных базисных функций

Шаг 4

Рассмотрим степень ортогональности сигнала контейнера С к полученным базисным функциям , для чего воспользуемся программным модулем (М.91).

Результат вычисления модуля (М.91) изображен на рис. 5.54. При выбранном контейнере и алгоритме формирования массива максимальное абсолютное значение погрешности ортогональности 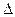составляет 312.

Рис. 5.54. График оценки степени ортогональности массива контейнера С к базисным функциям

Шаг 5

Пусть скрываемое сообщение — М :="© Пузыренко А.Ю., 2005г.". Двоичный объем сообщения составляет бит что не превышает общего количества базисных функций .

Используя программный модуль (М.92), проведем модуляцию сообщения М базисными функциями (см. формулу (5.47)), предварительно присвоив тем элементам двоичного вектора сообщения, которые имели нулевое значение, значение -1.

Рис. 5.55. Пример модулированного сообщения

Результат модуляции приведен на рис. 5.55. Присутствие на рис. 5.55 полностью черных сегментов говорит о том, что некоторые базисные функции не принимали участия в модуляции по причине отсутствия в сообщении бит с соответствующими им индексами. В данном случае количество неиспользованных базисных функций:

Шаг 6

С учетом максимального значения погрешности 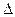, проведем вычисление достаточного коэффициента усиления мощности встроенного в контейнер модулированного сообщения: Для этого используем специальный вычислительный модуль решения неравенств (М.93).

Данный модуль открывается директивой Given, после которой следует логическое неравенство, в выполнении которого мы заинтересованы. Функция Find(K_G) возвращает минимальное значение переменной К_G, предварительно заданной как K_G := 1. позволяющее получить точное решение неравенства. Полученный результат с помощью функции округляется до наименьшего целого, превышающего точное решение.

Шаг 7

Принимая во внимание значение коэффициента К_G, проводим предварительное нормирование массива контейнера, используя программный модуль (М.94),

Без проведения такой операции весьма вероятны случаи, когда в результате встраивания данных в контейнер значения яркостей отдельных пикселей последнего выйдут за пределы диапазона [0,255]. При этом яркость 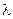будет вычисляться с помощью функции записи в файл изображения как значение А это вызовет ощутимый зрением человека скачок значения яркости через весь диапазон ее изменения и, очевидно, является недопустимым[11].

До нормирования имеем: min(C)=0, mах(С)=255. После выполнения модуля (М.94): min(C_norm) = 5, max(C_norm) = 250.

Очевидно, что даже в случае прибавления к граничным значениям яркости пикселя контейнера элемента сообщения, модулированного определенной базисной функцией (который может принимать значение ), яркость пикселя заполненного контейнера не выйдет за допустимые пределы (рис. 5.56):

; при этом ,.

Шаг 8

Для извлечения сообщения должны быть, известны:

• стеганоконтейнер S*;

• размерность контейнера X* и Y*;

• общее количество базисных функций ;

• конфигурация (в простейшем случае — n*) и алгоритм получения базисныхфункций

Рис. 5.56 Пустой (С), нормированный (С_norm) и заполненный при К_G=5(S) контейнеры

Программный модуль извлечения скрытого путем расширения спектра прямой последовательностью сообщения — (М.95).

Результат вычисления показателей искажения контейнера сведен в табл. 5.5 (стр. 189).

Более эффективным, по мнению авторов [88], является алгоритм реализации метода РСПП, который заключается в использовании «двойного канала» встраивания: каждая базисная функция по заранее оговоренному алгоритму делится на две равные значащие части, которые модулируются последовательностями (-1)(+1) для встраивания "0", и (+1)(-1) для встраивания "1". При извлечении сообщения из контейнера, каждый бит является результатом двойной демодуляции — для случаев (-1)(+1) и (+1)(-1) проводится вычисление значений функции корреляции. Очевидно, что истинное (при идеальном канале связи) значение бита сообщения ("0" или "1") будет определяться большим значением корреляции.

Реализация приведенного алгоритма требует внесения изменений в блоки "(*)" программных модулей встраивания (М.92) и извлечения (M.95). Возможный вариант замены представлен фрагментами программных модулей (М.96), (М.97).

Как на этапе встраивания, так и во время извлечения, для деления значащих элементов базисных функций на два подмножества используется значение переменной-счетчика V, которая в первом случае (см. модуль (М.96)) представлена как вектор.

Таблица 5.5 Показатели визуального искажения в случае скрытия данных методом расширения спектра

Название показателя искажения	Оригинал	РСПП-1	РСПП-2
Максимальная разность. МD
Средняя абсолютная разность. AD		4.614	4.624
Нормированная средняя абсолютная разность, NAD		0.031	0.032
Среднеквадратическая ошибка MSE		31.721	31.817
Нормированная cреднеквадратическая ошибка HMSE		1.101·10-3	1.104·10-3
Lp- норма, р=2		5.632	5.641
Лапласова cреднеквадратическая ошибка LMSE		0.113	0.102
Отношение "сигнал/шум" SNR	∞	908.381	905.628
Максимальное отношение "сигнал/шум", PSNR	∞	2.050·103	2.044·103
Качество изображения ІF		0.998899	0.998896
Нормированная взаимная корреляция NC		0.986079	0.986052
Качество корреляции СQ	196.672	193.934	193.929
Структурное содержание SC		1.027477	1.027529
Общее сигма-отношение "сигнал/шум" GSSNR	∞	566.540	563.058
Сигма-отношение "сигнал/шум" SSNR	∞	103.8	103.5
Нормированное отношение "сигма/ошибка" NSER
Подобие гистограмм HS

Значения показателей искажения контейнера в случае использования данного алгоритма занесены в табл. 5.5.