Лабораторная работа № 10 Гетероскедастичность и взвешенный метод наименьших квадратов

Цель: научиться оценивать наличие эффекта гетероскедастичности и использовать взвешенный метод наименьших квадратов.

Основные формулы и понятия:

Тест ранговой корреляции Спирмена

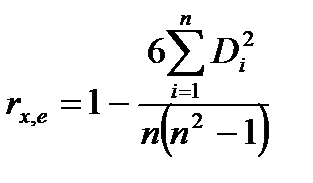— коэффициент ранговой корреляции Спирмена,

где x — одна из объясняющих переменных, 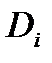— разность между рангом i-го наблюдения x и рангом модуля остатка в i-м наблюдении.

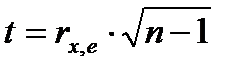— статистика.

Если в модели регрессии имеется более одной объясняющей переменной, то проверка гипотезы может выполняться с использованием каждой из них.

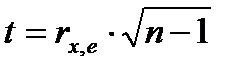— статистика

Условие принятия гипотезы .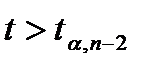

Если данное условие выполняется, то нулевая гипотеза о наличии гетероскедастичности будет принята при уровне значимости a.

Тест Голдфельда — Кванта

В этом случае все наблюдения необходимо упорядочить по мере возрастания значений x. Затем построить регрессионную модель для первых m и последних m наблюдений. Соответственно обозначим через ESS₁ и ESS₂ необъясненную сумму квадратов отклонений в каждой регрессии. Тогда статистика имеет вид

.

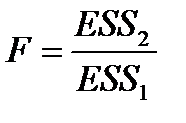Если выполняется условие 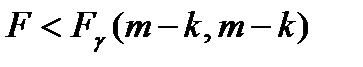, то гипотеза об отсутствии гетероскедастичности отвергается.

Взвешенный метод наименьших квадратов основан на минимизации суммы:

.

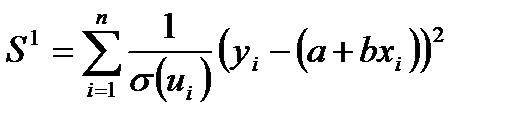Электронная таблица Excel

К сожалению, в электронной таблице нет дополнительных инструментов, которые позволяли бы проверять гипотезы и реализовывать взвешенный метод наименьших квадратов. Однако данные тесты можно реализовать вручную. Так, например, для теста ранговой корреляции Спирмена необходимо выполнить следующие действия:

1.Отсортировать данные в таблице по возрастанию значений x, для чего необходимо выбрать пункт меню Данные, Сортировка, а затем выбрать столбец, в котором находятся значения x;

2.Придать каждому наблюдению ранг, для чего необходимо добавить новый столбец, в котором задать числа от 1 до n;

3.Вызвать из пакета анализа надстройку Регрессия, указав в диалоговом окне опцию Остатки. После выполнения данной надстройки появится дополнительная таблица, в которой содержатся номера наблюдений, прогнозы и остатки. Тот столбец таблицы, в котором находятся остатки, необходимо перенести к исходным данным. После выполнения этих действий наша таблица будет содержать четыре столбца: ранг наблюдения, упорядоченные значения регрессора x, значения y и значения остатков;

4.Отсортировать данные по возрастанию модулей остатков и добавить новый столбец рангов остатков, аналогичным образом задав значения от 1 до n;

5.В дополнительном столбце вычислить значения разности между двумя полученными рангами (это и будет значение D_i);

6.На основании формул подсчитать коэффициент ранговой корреляции и статистику;

7. Проверить гипотезу можно посредством функции, которая вычисляет значение двусторонней критической точки распределения Стьюдента (лабораторная работа № 3).

Если выполнить данные действия для таблицы 1, то получим таблицу 20.

Таблица 20 Расчетная таблица

Ранг по x	Ценаx1(т.)	Спрос y (тыс. шт.)	Остатки	Ранг по остаткам	Разность рангов Di	Di* Di
	15,49т.	116,9143034	–3,7319
	16,33т.	111,4565323	–2,67328
	15,62т.	118,068067	–1,5813
	16,69т.	110,1056432	–1,31194
	15,92т.	116,169908	–1,12322
	15,28т.	121,1749683	–1,11646		–3
	16,76т.	110,023139	–0,84306
	15,54т.	119,8642978	–0,39014		–3
	15,91т.	117,0876924	–0,34387		–1
	15,21т.	123,8094363	1,019821		–8
	15,95т.	118,3436007	1,257187		–1
	15,09т.	125,177912	1,426776		–11
	16,31т.	116,2008486	1,847847		–2
	16,60т.	115,102583	3,003645		–1
	15,70т.	123,5886637	4,559903		–8
					Сумма

Следовательно, значение ранговой корреляции Спирмена будет равно

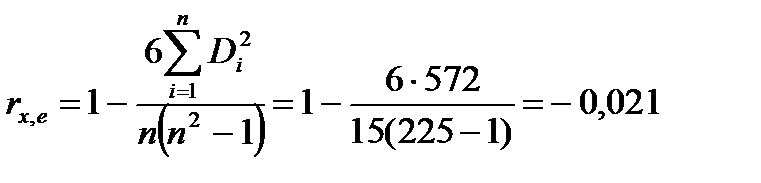
А значение статистики будет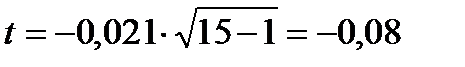

Выбрав уровень значимости 5 %, получаем критическую точку 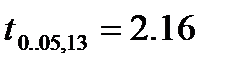. Данное значение получено формулой СТЬЮДРАСПОБР(0,05;13).

Поскольку условие 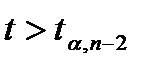не выполняется, то гипотеза о наличии гетероскедастичности будет отклонена.

Для проверки подобной гипотезы на основании теста Гольдфельда — Кванта необходимо подобным образом отсортировать наблюдения по возрастанию значения x, а затем отдельно оценить каждую регрессионную модель для первой трети и для последней трети наблюдений, вычислив при этом объясненную сумму квадратов отклонений, получив тем самым значения. А затем просчитать статистику.

Используя вышеописанные вычисления можно, хотя это достаточно трудно, проверить модель на гетероскедастичность, однако нет принципиальных методов для реализации взвешенного метода наименьших квадратов. Поэтому рассмотрим программные пакеты, предназначенные специально для статистических вычислений. В настоящее время имеется большое количество таких программ, разнообразных как по внешнему интерфейсу, так и количеству предлагаемых возможностей. Мы остановимся на пакете SPSS for Windows поскольку интерфейс данной программы во много похож на Excel.