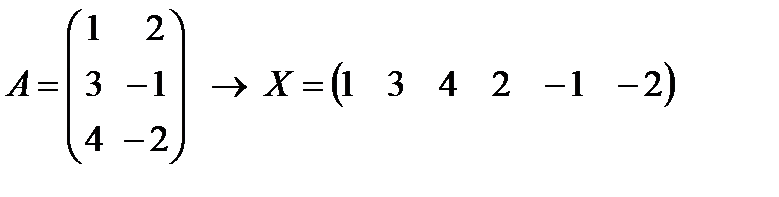Лабораторная работа № 6 Обработка матриц

Цель работы: Научиться разрабатывать алгоритмы обработки многомерных массивов и создавать проектную документацию к своим программам.

Задание: Разработать алгоритм и составить программу, обрабатывающую двумерный массив в соответствии с указанным в варианте заданием. Разработать документацию к программе , в которой необходимо указать назначение программы, требования к вводимым данным , формат выводимой информации и дать описание алгоритма решения задачи . Документация должна отражать все решения , принятые в процессе разработки и реализации программы.

Варианты заданий

1. Определить номер строки и номер столбца элемента прямоугольной матрицы 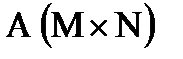, ближе всего расположенного к 0.

2. Найти сумму элементов прямоугольной матрицы 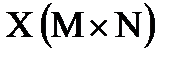, находящихся на периметре этой матрицы.

3. Сформировать вектор 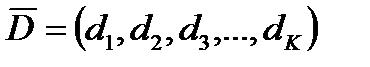, каждый элемент которого равен среднему арифметическому значений элементов строк матрицы С размерностью .

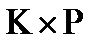4. В заданной матрице 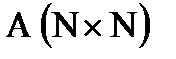элементы каждой строки (кроме диагональных элементов) заменить средним арифметическим диагональных элементов этой строки

5. Вычислить элементы вектора 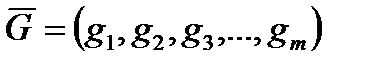как произведение элементов соответствующих строк заданной матрицы А размерностью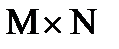

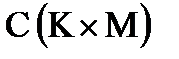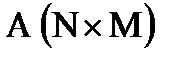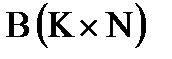6. Рассчитать элементы матрицы , являющейся произведением матриц и . Элементы матрицы С рассчитываются по формуле

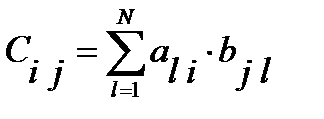
7. Рассчитать элементы матрицы 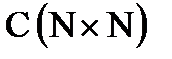по формуле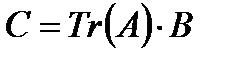

где 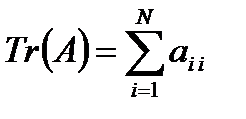– след матрицы ;

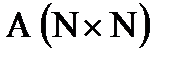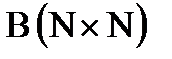– исходная матрица

8. Подсчитать количество нулевых элементов матрицы 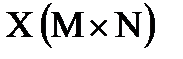, лежащих на диагоналях, и напечатать их индексы.

9. В заданной матрице 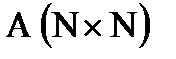поменять местами элементы главной и побочной диагоналей относительно горизонтальной средней линии.

10. Определить, в какой из четвертей матрицы 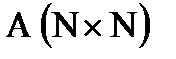сумма элементов наибольшая, а в какой – наименьшая (за исключением диагональных элементов).

11. Сформировать вектор 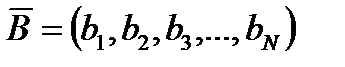, каждый элемент которого определяется как минимальный элемент соответствующего столбца исходной матрицы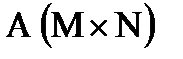

12. Преобразовать исходную матрицу 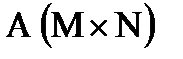так, чтобы последний элемент каждой строки был заменен суммой предыдущих элементов той же строки.

13. Получить вектор 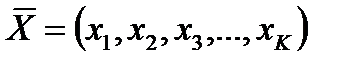, каждый элемент которого равен сумме элементов соответствующей строки заданной матрицы .

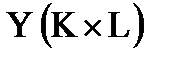14. Рассчитать элементы массива Z как произведения элементов соот­ветствующих столбцов исходной матрицы .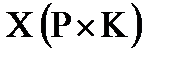

15. Преобразовать заданную матрицу 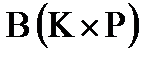таким образом, чтобы первый элемент каждого столбца был заменен произведением последую­щих элементов того же столбца.

16. Преобразовать матрицу 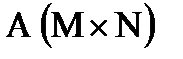так, чтобы все элементы, располо­женные ниже главной диагонали, были уменьшены вдвое, а элементы рас­положенные выше главной диагонали, - увеличены вдвое.

17. Определить количество отрицательных элементов в левой и правой четвертях заданной матрицы .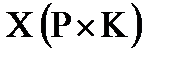

18. Найти отношение минимального элемента матрицы 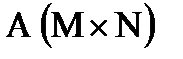и мак­симального элемента матрицы .

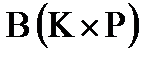19. В матрице 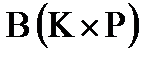найти сумму положительных элементов, расположенных в верхней и нижней четвертях.

20. Сформировать вектор 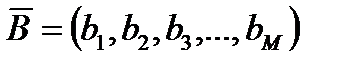, каждый элемент которого определяется как максимальный элемент соответствующей строки заданной матрицы .

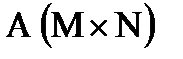21. В прямоугольной матрице 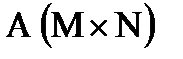поменять местами минимальный элемент, расположенный на главной диагонали, и максимальный элемент, расположенный на побочной диагонали.

22. В заданной матрице 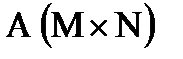найти нулевой элемент с наибольшим значением индекса i и все элементы столбца, в котором находится этот элемент, обнулить. Если в матрице нет нулевых элементов, отпечатать со­ответствующее сообщение.

23. Найти отношение количества положительных элементов к количеству отрицательных элементов заданной матрицы 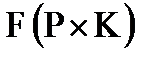. В случае, если матрица F не содержит отрица­тельных элементов, отпечатать соответствующее сообщение.

24. В каждой строке матрицы 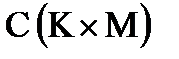поменять местами элементы главной и побочной диагоналей.

25. Для квадратной матрицы 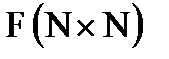найти отношение суммы элемен­тов, расположенных выше главной диагонали, к сумме элементов распо­ложенных ниже главной диагонали, предусмотрев соответствующее сооб­щение, если последняя сумма окажется равной нулю.

26. Определить оценки дисперсии для каждой строки заданной матрицы 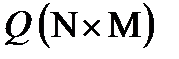. Оценка дисперсии каждой строки определяется по формул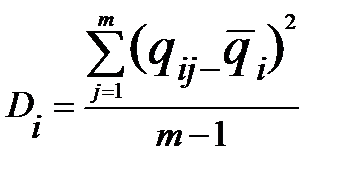е , где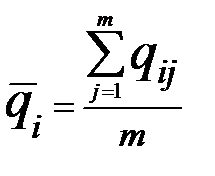

27. Получить массив 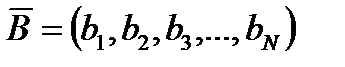, каждый элемент которого равен среднему арифметическому значений элементов соответствующего столбца матрицы .

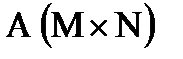28. В заданной матрице 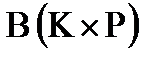найти элемент 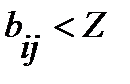, с наибольшим значением индекса j и все элементы столбца, в котором находится искомый элемент (кроме него), сделать равными единице. Значение Z вводится с клавиатуры

29. Транспонировать заданную матрицу 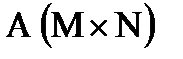. Операция транспонирования заключается в том, что строки и столбцы в исходной матрице меняются местами. Например

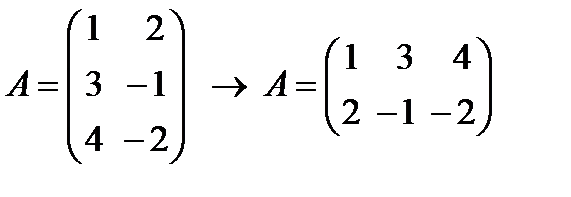
30. Преобразовать заданную прямоугольную матрицу 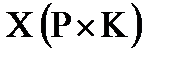в матрицу- строку 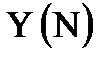, расположив последовательно все столбцы матрицы X. Например