РЕШЕНИЕ ЗАДАЧИ С ИСПОЛЬЗОВАНИЕМ FlexPDE (часть 2)
Пример расчета установившихся колебаний для двутаврового профиля в окрестности первых двух частот дается в файле St2LH_AFC.pde.
АНАЛИЗ РЕЗУЛЬТАТОВ, полученных в ANSYS (часть 2)
Построенная конечно-элементная модель с граничными условиями для гармонического анализа показана на рис. 6.
Рис. 6 Конечно-элементная модель с граничными условиями
для гармонического анализа
Амплитудно-частотную характеристику можно построить в постпроцессоре /POST26.Рассмотрим верхний левый угол двутавра - узел с координатами (-l, b). Выведем для этого узла график зависимости перемещения uy от частоты (рис. 7).
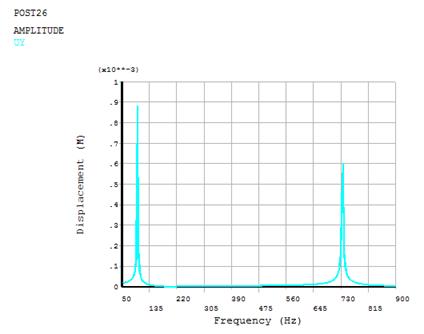
Рис. 7 Амплитудно-частотная характеристика двутаврового профиля
Точные значения резонансных частот можно определить, просмотрев файл, содержащий значения точек графика (TimeHist PostPro->Variable Viewer, выбрать переменную UY, кнопка List Data). Ниже приведен листинг части этого файла.
***** ANSYS POST26 VARIABLE LISTING *****
FREQ 20 UY
UY
AMPLITUDE PHASE
53.400 0.192111E-04 -0.366623E-01
56.800 0.201293E-04 -0.415987E-01
60.200 0.212289E-04 -0.474073E-01
63.600 0.225622E-04 -0.543564E-01
67.000 0.242043E-04 -0.628316E-01
70.400 0.262671E-04 -0.734075E-01
73.800 0.289249E-04 -0.869796E-01
77.200 0.324650E-04 -0.105024
80.600 0.373967E-04 -0.130159
84.000 0.447163E-04 -0.167510
87.400 0.566731E-04 -0.228648
90.800 0.796403E-04 -0.346371
94.200 0.141561E-03 -0.664503
E-03 -4.48547
101.00 0.188938E-03 -178.962
104.40 0.816375E-04 -179.513
107.80 0.505037E-04 -179.673
111.20 0.356966E-04 -179.748
114.60 0.270504E-04 -179.791
………………………………………………………………………………………………………………………………………………………
FREQ 20 UY
AMPLITUDE PHASE
699.40 0.256776E-04 -0.553062
702.80 0.281820E-04 -0.613947
706.20 0.312687E-04 -0.689105
709.60 0.351675E-04 -0.784179
713.00 0.402479E-04 -0.908233
716.40 0.471431E-04 -1.07681
719.80 0.570376E-04 -1.31898
723.20 0.724321E-04 -1.69614
726.60 0.996742E-04 -2.36424
730.00 0.160950E-03 -3.86911
733.40 0.423414E-03 -10.3615
E-03 -164.979
740.20 0.178516E-03 -175.532
743.60 0.103845E-03 -177.367
747.00 0.729001E-04 -178.126
750.40 0.559803E-04 -178.540
753.80 0.453134E-04 -178.801
757.20 0.379738E-04 -178.981
760.60 0.326147E-04 -179.111
Видно, что наибольшие значения амплитуды перемещения наблюдаются на резонансных частотах fr1 = 97.6 (Гц) и fr2 = 736.8 (Гц). Данные значения частот резонансов близки к значениям собственных частот f1 = 98.2 (Гц) и f2 = 735.4 (Гц).
Далее выведем картины деформированных форм колебаний на резонансных частотах. Для этого нужно предварительно считать результаты для сета с соответствующим значением частоты (General PostProc->Read Results->By Pick). Для каждого рассчитываемого значения частоты имеем два сета, соответствующие вещественной и мнимой части соответствующего вектора перемещений.
Нас рис. 8 представлены деформированные формы для вещественной и мнимой частей вектора перемещений на частоте fr1 = 97.6 (Гц). Видно, что эти деформированные формы совпадают между собой с точностью до знака. При этом деформированная форма для мнимой части вектора перемещений совпадает с формой колебаний, соответствующей первой собственной частоте f1 = 98.17 (Гц).
Нас рис. 9 представлены деформированные формы для вещественной и мнимой частей вектора перемещений на частоте fr2 = 736.8 (Гц). Видно, что эти деформированные формы совпадают между собой, а также с точностью до знака совпадают с формой колебаний, соответствующей второй собственной частоте f2 = 735 (Гц).
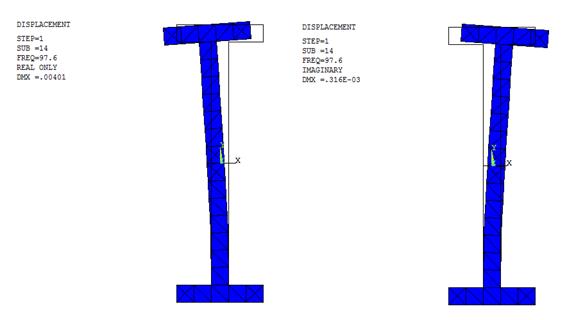
Рис. 8 Формы колебаний на первой резонансной частоте (ANSYS)
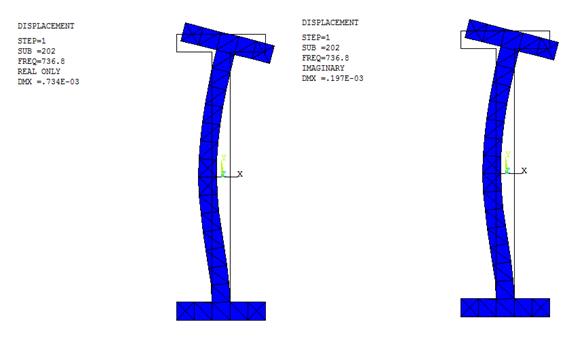
Рис. 9 Формы колебаний на второй резонансной частоте (ANSYS)
