Программирование циклических алгоритмов

Циклическим алгоритмом (или просто циклом) называется алгоритм, содержащий вычисления, повторяющиеся при различных значениях некоторой переменной, названной параметром цикла, а сами повторяющиеся вычисления составляют тело цикла.

Типы циклов.По способам организации цикла можно выделить:

а) цикл типа арифметической прогрессии;

б) итерационный цикл.

Особенностью цикла типа арифметической прогрессии является изменение параметра цикла по закону арифметической прогрессии, и поэтому можно, не выполняя цикла, определить количество повторений цикла.

Пример 3.3.1. Сформировать вектор z из n элементов, определяемых соотношением:

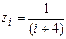, i = 1, …, n; n = 10.

В этом примере i – параметр цикла, а тело цикла (вычисление элементов 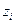) будет повторено n = 10 раз, т.е. алгоритм является циклом типа арифметической прогрессии. ¨

В итерационном цикле невозможно «априори», т.е. не выполняя вычислений, определить число повторений тела цикла из-за разнообразных условий завершения цикла.

Пример 3.3.2. Вычислить приближенное значение 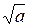, используя итерационную процедуру:

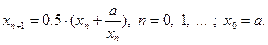(3.3.1)

В качестве приближенного значения 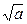принимается 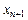, удовлетворяющее условию:

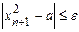, (3.3.2)

где 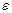– заданная точность вычисления корня квадратного. Даже задав конкретные значения 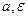(например, а = 9, 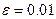), невозможно априори определить количество повторений цикла. ♦

Программирование цикла типа арифметической прогрессии.Параметр такого цикла задается дискретной переменной (называемой также ранжированной переменной), и тогда конструкции, входящие в тело цикла, располагаются начиная от этого описания и до конца документа MathCAD или до конструкции, переопределяющей дискретную переменную – параметр цикла.

Фрагмент документа, в котором реализован алгоритм решения задачи примера 3.3.1 приведен на рис. 3.3.1.

Рис. 3.3.1. Формирование вектора z примера 3.3.1

На рис. 3.3.2 приведен фрагмент документа, формирующий матрицу (двумерный массив) по следующему правилу:

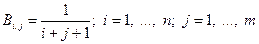. (3.3.3)

Очевидно, что этот цикл имеет уже два параметра: i – параметр, определяющий номер строки; j – параметр, определяющий номер столбца матрицы. Напомним, что такой цикл называется двойным циклом.

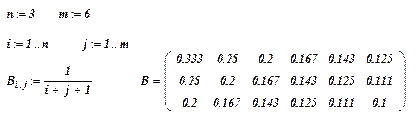
Рис. 3.3.2. Формирование матрицы В по алгоритму (3.3.3)

Заметим, что в приведенных на рис. 3.3.1 и 3.3.2 фрагментах системная переменная ORIGIN=1.

Программирование итерационных циклов.Для этого используется функция until, записываемая в виде:

until (<выр. 1>,<выр. 2>).

Эта функция принимает значение равное выр. 2 , если выр. 1 больше или равно 0. Как только выр. 1 принимает отрицательное значение, функция until принимает значение0, и дальнейшее выполнение функции прекращается. Это свойство позволяет применять функцию until для программирования итерационных циклов.

На рис. 3.3.3 приведен фрагмент документа, реализующий алгоритм примера 3.3.2. ♦

Замечание 3.3.1. В русифицированной версии MathCAD2001i обращение к этой функции вызывает ошибку и рекомендуется для программирования итерационных циклов использовать подпрограмму-функцию с оператором while.

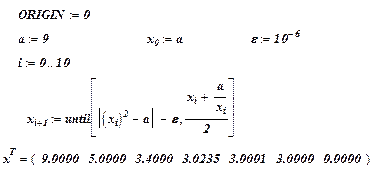
Рис. 3.3.3. Приближенное вычисление корня квадратного

с помощью функции until

Последний, 7-й элемент массива x (значение индекса равно 6) равен нулю из-за того, что выражение 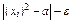стало меньше нуля, а значение функции until – 0. Поэтому в качестве приближенного значения корня необходимо принять предыдущий элемент, номер и значение которого определяются в следующем фрагменте:

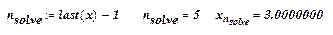
Следует отметить, что такой способ программирования не эффективен при большом числе итераций из-за необходимости хранить в памяти все предыдущие значения x_n. На самом деле необходимо хранить в памяти только два приближения: x_n («старое») и x _n+1 («новое»).

В заключение этого параграфа заметим, что рассмотренные способы безмодульного программирования можно рекомендовать для реализации достаточно простых алгоритмов. Более сложные алгоритмы целесообразно реализовать в виде подпрограммы-функции, которая содержит конструкции, подобные конструкциям таких алгоритмических языков, как FORTRAN или Pascal: оператор присваивания, условные операторы, операторы цикла и т.д. В следующих темах будут рассмотрены конструкции пакета MathCAD, позволяющие реализовывать различные алгоритмы в подпрограмме-функции.