Общие комментарии по поводу кросс-табуляции
Можно построить таблицу сопряженности больше, чем для трех переменных, но интерпретация полученных результатов достаточно сложная. Кроме того, поскольку число ячеек многократно увеличится, проблематично оставить необходимое количество респондентов или случаев в каждой ячейке. Как правило, чтобы вычислить статистику в каждой ячейке, должно быть, по крайней мере, пять наблюдений. Таким образом, кросс-табуляция — неэффективный способ проверки связей для ситуаций с несколькими переменными, она рассматривает просто связь между переменными, а не причинность. Чтобы изучить причини следственную связь, необходимо провести соответствующее причинно-следственное исследование (см. главу 7).
СТАТИСТИКИ ТАБЛИЦ СОПРЯЖЕННОСТИ ПРИЗНАКОВ
Мы рассмотрим статистики, обычно используемые для оценки статистической значимости и тесноты связи переменных, содержащихся в таблице сопряженности. Статистическая значимость наблюдаемой связи обычно измеряется критерием хи-квадрат. Теснота связи важна с практической точки зрения. Обычно она имеет значение, если связь статистически значимая. Тесноту связи можно измерить коэффициентом корреляции фи, коэффициентом сопряженности признаков, V-коэффициентом Крамера и коэффициентом "лямбда". Эти статистики ниже описаны детальнее.
Критерий хи-квадрат
Критерий хи-квадрат(chi-square statistic, Х2) используют для проверки статистической значимости наблюдаемой связи в таблице сопряженности признаков.
Критерий хи-квадрат (chi-square statistic, Х2)
Критерий, используемый для проверки статистической значимости наблюдаемых связей в таблицах сопряженности признаков. Он помогает определить наличие или отсутствие систематической связи между двумя переменными.
Он помогает определить наличие или отсутствие систематической связи между двумя переменными. В данном случае нулевая гипотеза Н0 утверждает, что между двумя переменными не существует никакой связи. Проверка нулевой гипотезы выполняется вычислением частот распределения признаков анализируемых переменных в ячейках таблицы, которые можно было бы ожидать, если бы не существовало зависимоста между переменными, и при данных итоговых числах в каждом ряду и колонке. Затем для вычисления значения Х2 эти ожидаемые частоты, обозначаемые 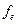 , сравнивают с фактически наблюдаемыми частотами распределения признаков
, сравнивают с фактически наблюдаемыми частотами распределения признаков 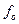 , соответствующими ячейкам таблицы. Чем больше разница между ожидаемыми и фактическими частотами, тем выше значение статистики. Предположим, что таблица сопряженности имеет г рядов и с колонок, а случайная выборка состоит из п наблюдений. Tогда ожидаемую частоту для каждой ячейки вычислим по следующей формуле:
, соответствующими ячейкам таблицы. Чем больше разница между ожидаемыми и фактическими частотами, тем выше значение статистики. Предположим, что таблица сопряженности имеет г рядов и с колонок, а случайная выборка состоит из п наблюдений. Tогда ожидаемую частоту для каждой ячейки вычислим по следующей формуле:
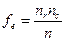
где пr - итоговое число в ряду, пс — итоговое число в колонке, п — полный размер выборки.
Для данных табл. 15.3 ожидаемая частота распределения признаков для ячеек, расположенных слева направо и сверху вниз, выглядит так:
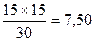
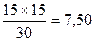
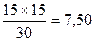
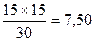
Тогда значение Х2 вычисляют следующим образом:
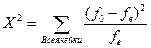
Для данных табл. 15.3 значение Х2 вычислили по формуле:
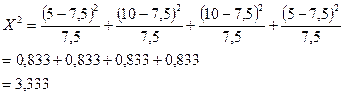
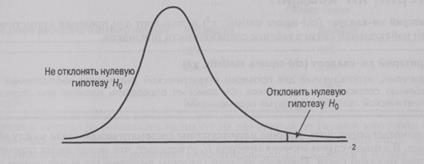
Чтобы определить, существует ли между переменными систематическая связь, определяют вероятность получения значения Х2, равного или большего, чем рассчитанное из таблицы сопряженности. Важной характеристикой критерия Х2 является число степеней свободы (df). В общем случае оно равно числу наблюдений за вычетом числа ограничений, необходимых для вычисления статистического показателя. Для критерия хи-квадрат таблицы сопряженности число степеней свободы равно произведению количества рядов ( r ) минус единица на количество колонок(с ) минус единица, т.е. df = (r-l)x(c-l) [11]. Нулевая гипотеза (H0) об отсутствии зависимости между двумя переменными должна быть отклонена только тогда, когда полученное значение X2 больше, чем критическое значение X2 распределения с соответствующим числом степеней свободы, как это показано на рис. 15.8.
Критическое значение X
Рис. 15.8. Проверка зависимости между переменными с
помощью критерия X2
Распределение X2 (chi-square distribution) представляет собой асимметричное распределение, форма которого зависит исключительно от числа степеней свободы [12]. С ростом числа степеней свободы распределение хи-квадрат становится более симметричным. Данные табл. 3 в Статистическом приложении дают представление о величине X2 для различных степеней свободы. В этой таблице значение вверху каждой колонки указывает область в верхней части (правая сторона на рис. 15.8) распределения хи-квадрат. Например, для одной степени свободы и α = 0,05 значение X2 равно 3,841. Это означает, что для одной степени свободы вероятность превышения значения X2, равного 3,841, составляет 0,05. Другими словами, при уровне значимости, равном 0,05, и числе степеней свободы, равном единице, критическое значение статистики X2 равно 3,841.
Распределение X2 (Chi-square distribution)
Асимметричное распределение, форма которого зависит исключительно от числа степеней свободы. С ростом числа степеней свободы хи-квадрат распределение более симметрично.
Для таблицы сопряженности (табл. 15.3) число степеней свободы равно (2 — 1) х (2 - 1) = 1. Вычисленное значение X2 — 3,333. Так как оно меньше критического значения, равного 3,841, нулевую гипотезу об отсутствии связей между переменными нельзя отклонить. Это означает, что связь между переменными не является статистически значимой при уровне значимости, равном 0,05.
Статистику хи-квадрат также можно использовать в проверках степени согласия, чтобы определить, согласуется ли определенная модель с наблюдаемыми данными. Эти проверки выполняют вычислением значимости (уровня статистической значимости) выборочных отклонений от предполагаемых теоретических (ожидаемых) распределений, а также можно выполнить как на основе таблиц сопряженности, так и на основе таблиц распределения частот (одномерная табуляция). Расчет х2 и определение ее уровня статистической значимости выполняется изложенным выше способом.
Значение X2 следует вычислять только для числовых данных. Если данные представлен в виде процентов, то сначала их необходимо перевести в абсолютные единицы или числа. Кроме того, допущение, лежащее в основе проверки с помощью критерия X2, заключается в том, что наблюдения проведены независимо. В качестве общего правила стоит запомнить, что проверку по критерию хи-квадрат нельзя выполнять, если ожидаемые или теоретические частоты в любой из ячеек меньше пяти. Если число наблюдений в любой ячейке меньше десяти, или если таблица имеет два рядка и две колонки (таблица 2 х 2), то необходимо использовать поправочный коэффициент [13]. С поправочным коэффициентом значение X2 равно 2,133, что не является значимым при уровне значимости, равном 0,05. Для таблицы размером 2x2, статистику хи-квадрат называют фи-коэффициентом.
Фи-коэффициент
Фи-коэффициент (phi coefficient, ф) используют для измерения тесноты связи в особом случае — при анализе таблицы с двумя рядками и двумя колонками (таблица 2 х 2).
Фи-коэффициент (phi coefficient, φ)
Мера тесноты связи переменных для конкретного вида таблицы: с двумя рядками и двумя колонками (таблица 2 х 2).
Фи-коэффициент пропорционален корню квадратному из Х2. Для выборки размером п эту статистику находят по формуле:
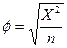
Фи-квадрат принимает значение, равное 0, если связь отсутствует, на что также указывает и значение хи-квадрат, равное 0. При сильной связи между переменными фи-коэффициент имеет значение 1 и все наблюдения находятся на главной или второстепенной диагонали. (В некоторых компьютерных программах фи-коэффициент принимает значение -1, а не +1, когда наблюдается отрицательная связь.) В нашем случае фи-коэффициент равен:
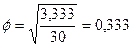
Таким образом, связь не очень сильна. В более общем случае при наличии таблицы любого размера тесноту связи можно оценить коэффициентом сопряженности признаков.
