Минимизация конечного автомата

Учитывая, что мы можем определять эквивалентные автоматы, хотелось бы научиться находить наименьший среди них. Задача нахождения наименьшего конечного автомата, распознающего данный язык, также разрешима, причем тоже конструктивным образом. Для описания процесса нахождения наименьшего конечного автомата, введем следующее определение.

Определение. Строка w различает состояния s и t, если существует такая входная цепочка w, что d(s,w) является заключительным состоянием, а состояние d(t,w) не является заключительным состоянием, или, наоборот, d(s,w) не является заключительным состоянием, а состояние d(t,w) является заключительным состоянием.

Очевидно, что если некоторая строка w различает состояния t₁ и t₂ такие, что t₁=d(q_i,a) и t₂=d(q₂,а), то строка aw различает состояния q₁ и q₂.

Теперь перейдём к описанию процесса минимизации конечного автомата.

1. Мы начнём с поиска и удаления всех недостижимых состояний.

2. Затем мы должны найти такое разбиение множества состояний автомата, чтобы каждое подмножество содержало неразличимые состояния, т.е. если s и t принадлежат некоторому подмножеству, то для всех a из S d(s,a) и d(t,a) также принадлежат этому подмножеству. Для этого мы разобьём множество состояний на два подмножества: F и S-F.

3. В дальнейшем, мы попытаемся разбить каждое из подмножеств, соблюдая указанное выше условие. Если возникает ситуация, при которой мы не можем разбить никакое множество состояний, то мы заканчиваем процесс разбиения.

4. В результате мы получим некоторый набор множеств состояний S₁…S_k. Каждое из S_i содержит только неразличимые состояния.

5. Наконец, внесём в множество состояний минимизированного автомата по одному представителю каждого из множеств S_i. На этом процесс завершается.

Далее мы приведём пример минимизации автомата.

Пример минимизации конечного автомата

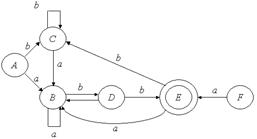
Рассмотрим процесс минимизации автомата, представленного на слайде. Согласно алгоритму, вначале мы произведем удаление недостижимых состояний – в нашем примере состояние F очевидно недостижимо и потому не попадет в минимизированный автомат.

Затем мы произведем разбиение множества состояний автомата на классы эквивалентности. Укажем такую последовательность разбиений:

1,E, ABCD

2, E, ABC, D, т.к. есть переход в Е

3, E, AC, B, D, т.к. есть переход в D

Таким образом, состояния A и C неразличимы. Поэтому получаем следующий автомат:

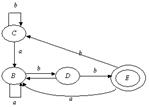
Алгоритм минимизации детерминированного конечного автомата
(эквивалентный начальному)

1, Находим и удаляем из начального автомата все недостижимые и непродуктивные состояния.

2, Все состояния конечного автомата разделяются на классы эквивалентности (0).

1. Все состояния, которые являются конечными в автомате (qi in F)

2. Все состояния, не вошедшие в F

3, Строим новое одно эквивалентное разбиение, выделив те состояния, которые по одинаковым символам переходят в 0 эквивалентные.

4, Повторяется шаг 3, последовательно создавая n+1 эквивалентное состояние по n эквивалентным, увеличивая так число классов эквивалентности.

5, Алгоритм заканчивается, когда n+1 эквивалентные состояния совпадают с n эквивалентными.

Каждый полученный класс эквивалентности будет новым состоянием в новом минимизированном автомате.

В множество F' автомата внесём те состояния, которые содержат хотя бы одно состояние из начального.

Пример.

Задан избыточный детерминированный KA=(S,Q,Q₀,d,F)

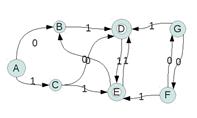
S={0,1}

Q={A,B,C,D,E,F,G}

F={D,E}

d: (d)

d(A,0)={B}

d(A,1={C}

d(B,1)={D}

d(D,1)={E}

d(E,1)={D}

d(D,0)={C}

d(E,0)={B}

d(C,1)={E}

d(G,1)={E}

d(G,0)={F}

d(F,0)={G}

d(F,1)={D}

Минимизация.

Первый шаг. Удаляем недоститжимые и непродуктивные состояния. В состояния F и G нельзя попасть, в них нет стрелок – они недостижимые.

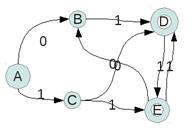
Строим 0 эквивалентные:

0-> (D,E), остальные → A, B, C

1-> (DE)(BC)(A) — из них можно попасть через один и тот же символ в (D,E)

2->(DE)(BC)(A)

Алгоритм завершён.

Строим новый автомат с состояниями (DE)(BC)(A)

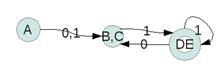
Пример. Задан избыточный детерминированный .

S={0,1,2}

Q={q₀,q₁,q₂,q₃,q₄,q₅,q₆,q₇,q₈}

F={q₆,q₇}

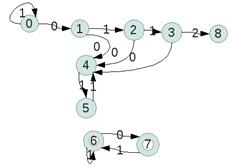
d: (d)

d(q₀,1)={q₀}

d(q₀,0={q₁}

d(q₁,1)=q₂

d(q₁,0)=q₄

d(q₂,1)=q₃

d(q₃,1)=q₁

d(q₂,0)=q₄

d(q₃,0)=q₄

d(q₃,2)=q₈

d(q₄,1)=q₅

d(q₄,0)=q₆

d(q₅,1)=q₄

d(q₅,0)=q₆

d(q₆,1)=q₆

q(q₆,0)=q₇

d(q₇,0)=q₇

d(q₇,1)=q₆

d(q₈,1)=q₈

Сразу удаляем q₈ – непродуктивный

0 → (q₆,q₇)(q₀,q₁,q₂,q₃,q₄,q₅)

1→ (q₆,q₇)(q₄,q₅)(q₀,q₁,q₂,q₃) из q₄,q₅ можно по 0 попасть в нулевой класс

2→ (q₆,q₇)(q₄,q₅)(q₁,q₂,q₃)(q₀)

3→ (q₆,q₇)(q₄,q₅)(q₁,q₂,q₃)(q₀)

Пример.

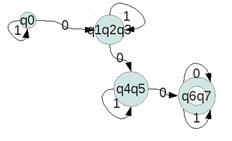
Результирующий автомат строится на основе первого, соединяя эквивалентные состояния в одно, внутренние переходы отображаются в виде петель.

Пример.

Q={0,1,3,4}

F={1,2}

d(0,a)=1

d(1,a)=3

d(1,b)=2

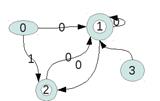
0→ (q₁,q₂),(q₀)

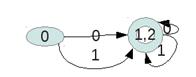
Удаляем q₅ и q₄, как непродуктивные состояния

После чего по алгоритму объединяем состояния

I (q₀q₂)(q₁q₃)

II (q₀q₂)(q₁q₃)

Строим минимальный автомат.