Моделирование недетерминированного конечного автомата

В этом примере показано, как абстрактную математическую конструкцию можно перевести на язык Prolog. Кроме того, данный пример показывает, что полученная в результате программа эмулятора конечного автомата может оказаться гораздо более гибкой, чем предполагалось первоначально.

Недетерминированным, конечным автоматом называется абстрактная машина, которая считывает в качестве входных данных строки символов и принимает реше­ние о том, следует ли принять или отвергнуть ту или иную входную строку. Конеч­ный автомат имеет целый ряд состояний и всегда находится в одном из состояний. Он способен изменять свое состояние, переходя из текущего в другое возможное со­стояние. Внутреннюю структуру конечного автомата можно представить с помощью графа переходов, подобного приведенному на рис. 4.3. В данном случае узлы графа Si, Зг. s?. и Si обозначают состояния автомата. Начиная с начального состояния (в этом примере — si), автомат переходит из одного состояния в другое, считывая входную строку. Направления переходов зависят от текущего входного символа; эти символы показаны в виде меток на дугах в графе переходов.

Переход происходит после чтения каждого входного символа. Следует отметить, что переходы могут быть недетерминированными. Например, если автомат, показан­ный на рис. 4.3, находится в состоянии Si и текущим входным символом является а,

Глава 4. Использование структур: примеры программ

он может перейти либо в л, либо в э₂. Некоторые дуги отмечены меткой null, кото­рая означает пустой символ. Такие дуги соответствуют так называемым скрытым переходам автомата. Подобные переходы называются скрытыми, поскольку они происходят без чтения входных данных, а наблюдатель, рассматривающий автомат как "черный ящик", не способен обнаружить, что произошел какой-либо переход.

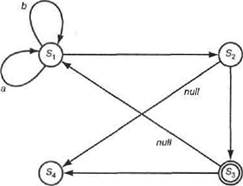
Рис. 4.3. Пример недетерминированного ко­нечного автомата

Состояние в, обозначено двойным кружком, который указывает на то, что это -конечное состояние. Считается, что автомат принимает входную строку, если в графе имеется путь перехода, такой, что

1. он начинается с начального состояния;

2. он оканчивается конечным состоянием;

3. метки дуг вдоль пути полностью соответствуют входной строке.

Задача принятия решения о том, какой из возможных переходов должен быть выполнен в тот или иной момент времени, полностью возложена на конечный авто­мат. В частности, автомат может выбрать вариант действий, предусматривающий или не предусматривающий выполнение скрытого перехода, если этот переход воз­можен в текущем состоянии. Но абстрактные недетерминированные машины такого рода имеют одно так называемое магическое свойство (т.е. свойство, не обусловлен­ное их структурой): если имеется выбор, они всегда выбирают "правильный" пере­ход, ведущий к принятию входной строки, если таковой существует. Например, ав­томат, показанный на рис. 4.3, принимает строки аЬ и aabaab, но отвергает строки abb и abba. Можно легко понять, что этот автомат принимает любую строку, кото­рая оканчивается на аЬ, и отвергает все прочие строки.

Б языке Prolog конечный автомат может быть задан с помощью трех описанных ниже отношений,

1. Унарное отношение final, которое определяет конечное состояние автомата.

2. Отношение trans с тремя параметрами, которое определяет переходы между состояниями таким образом:

trans(Sl, X, S2)

Это означает, что переход из состояния si в состояние sj возможен, если счи­тан текущий входной символ X.

3. Бинарное отношение
silent ( SI, SZ)

которое означает, что возможен скрытый переход из состояния s- в состояние э₂.

104 Часть I. Язык Prolog

Для конечного автомата, показанного на рис. 4.3, эти три отношения заданы сле­дующим образом:

final ( S3] . trans [ SI, a, SI) , trans t Si, a, S2] . trans ( Si, b, Si). trans{ S2, b, S3) . transt S3, b, S4). silentt S2, S4>.silent) S3, Si).

В дальнейшем входные строки будут представлены в виде списков Prolog. На­пример, строка aab будет представлена как [а, а,Ь]. Программа эмулятора конечно­го автомата, в которую введено описание этого автомата, должна обрабатывать за­данную входную строку и принимать решение о том, следует ли принять или отверг­нуть эту строку. По определению недетерминированный автомат принимает заданную строку (начиная с начального состояния), если после чтения всей входной строки автомат может (по всей вероятности) находиться в своем конечном состоянии.Программа эмулятора разрабатывается как бинарное отношение accepts, которое определяет, может ли быть принята некоторая строка из текущего состояния. Таким образом, предикат accepts ( State, String)

принимает истинное значение, если автомат, начиная с состояния State,рассматри­ваемого как начальное состояние, воспринимает строку String. Отношение accepts может быть определено тремя предложениями, которые соответствуют трем описан­ным ниже случаям.

1. В состоянии State принята пустая строка, [], притом что State является ко­нечным состоянием.

2. В состоянии State принята непустая строка, если чтение первого символа строки может перевести автомат в некоторое состояние, Statel, и остальная часть строки принята в состоянии Statel, как показано на рис. 4.4, а.

3. В состоянии State принята строка, если автомат может выполнить скрытый переход из состояния State в состояние Statel, а затем принять (всю) вход­ную строку в состоянии Statel, как показано на рис. 4.4, б.