Другие методы скрытия данных в неподвижных изображениях

Статистические методы

В основу статистических методов скрытия конфиденциальных данных положена модификация определенных статистических свойств изображения (или же его фрагментов) с последующей проверкой статистических гипотез во время извлечения для проверки, наличия указанных данных в контейнере. Сущность статистических методов сводится к такой модификации некоторых статистических характеристик контейнера, при которой принимающая сторона будет иметь возможность распознавать пустой контейнер от заполненного.

Как и в вышерассмотренных методах многоразрядную статистическую стеганосистему можно получить путем разбиения контейнера на достаточное количество непересекающихся блоков (в общем случае это количество равняется количеству бит 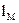в скрываемом сообщении): 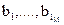. При этом, отдельный бит сообщения 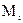.встраивается в і-й блок контейнера. Детектирование скрытого,' в блоке бита выполняется путем использования так называемой проверочной (тестовой) функции. Последняя позволяет распознавать наличие модификации блока:

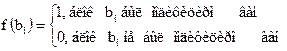
Получение функции f является наиболее проблематичной задачей при реализации статистического метода. Ее построение осуществляется на основе теории проверки статистических гипотез.

Для работы с данными, которые имеют двоичный формат, в большинстве случаев проводится манипулирование двумя гипотезами: основной — "блок b_i не был модифицирован", и альтернативной—"блок b_i был модифицирован"; При извлечении скрытых данных, функцию f последовательно применяют ко всем блокам контейнера. Если статистика контейнера превышает некоторое пороговое значение, то считается, что в блок было встроено "1", в противоположном случае — "0".

Статистические методы сложно применять на практике [3,89], Причинами этого являются, во-первых, необходимость располагать исчерпывающей статистикой 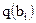для контейнера-оригинала, на основе которой принимаются решения о возможной модификации исследуемого контейнера (или его блока); во-вторых, распределение 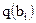должно быть заранее известно принимающей стороне, а в это в большинстве случаев является достаточно сложной задачей.

Питас (I. Pitas), в своей работе [89] предлагает использовать статистический метод для встраивания в полутоновое изображение С размерностью цифровой подписи представляет собой псевдослучайный двоичный шаблон размерностью , в котором количество "единиц" соответствует количеству "нулей":

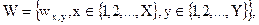(5.51)

где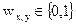

Оригинальное изображение представляется следующим образом

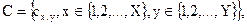(5.51)

где 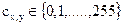- уровень интенсивности (яркости) пикселя (x,y)

Множество С разделяется на два подмножества, имеющих равную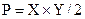

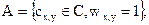(5.53)

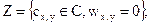(5.54)

Встраивание ЦВЗ W выполняется путем изменения всех элементов подмножества А на величину положительного целого коэффициента ;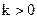

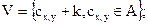(5.55)

, Изображение S с встроенным ЦВЗ получается путем объединения двух множеств:

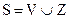(5.56)

Неизменность зрительного восприятия изображения (незаметность встроенных посторонних данных) предопределяемся законом Вебера-Фeхнера, а именно тем, что, величина коэффициента k, прибавляемого к яркости пикселя 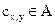для получения множества V, в основном является достаточно малой (с учетом 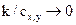) [75].

Автор [89] указывает на возможность довольно точного обнаружения встроенной информации путем исследования изменений, вызванных встраиванием. Главная идея при этом — экспертиза отличий средних значений (математических ожидани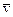й) и 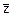двух выделенных подмассивов изображения V и Z. К результатам вычисления разности средних значений 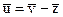применяется теория проверки гипотезы. Статистика, лежащая в основе критерия:

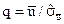(5.57)

где 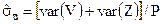; 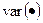— оценка дисперсии случайных переменных в соответствующем подмножестве.

Основная и альтернативная гипотезы, соответственно, представляют собой:

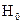: ЦВЗ в изображении отсутствует ;

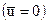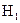: в изображение встроен ЦВЗ .

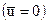Исходя из основной гипотезы, статистика q отвечает распределению Стьюдента с нулевым математическим ожиданием и (2·Р-2) степенями свободы, которое можно с достаточной точностью аппроксимировать нормальным распределением с нулевым математическим ожиданием и единичной дисперсией.

В случае альтернативной гипотезы, статистика q распределена по так называемому нецентрировавному распределению Стьюдента с математическим ожиданием 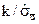. При значительном объеме выборки распределениеq может быть аппроксимировано нормальным распределением с единичной дисперсией и математическим ожиданием .

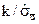Во время детектирования ЦВЗ возможны следующие две ошибки:

• ошибка первого рода: принято решение о наличии встроенного ЦВЗ, в то время как он в изображении отсутствует ("ложная тревога");

• ошибка второго рода: наличие встроенного ЦВЗ не установлено, хотя фактически он в изображении присутствует ("пропуск цели").

Если 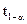в является t-процентилем, минимизирующим обе ошибки, то[12]

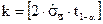(5.58)

как следствие, перед встраиванием ЦВЗ в контейнер существует возможность задаться степенью достоверности 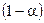, с которой на стадии детектирования можно сделать предположение об отсутствии или наличии встроенного в контейнер ЦВЗ.

Таким образом, предлагается следующий алгоритм встраивания ЦВЗ:

1. Подсчитываются значения 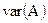и var(Z), которые используются для определения 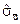, используя формулу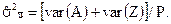

2. По формуле (5.58) вычисляется значение k. Следует заметить, что использованное в данной формуле квантование изменяет степень достоверности, сводя ее к некоторому значению 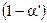. Кроме того, авторами было сделано предположение, что 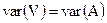что не является полностью справедливым по причине отсечений, возникающих в случае, когда результат действия 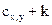выходит за пределы разрешенного диапазона [0; 255].

3. Создается "подписанное" ЦВЗ изображение Sпутем замены подмножества А из множества С на подмножество V (формулы (5.55), (5.56)).

Алгоритм детектирования ЦВЗ выглядит следующим образом:

1. Определяются математические ожидания 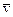и 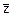выделенных подмассивов V и Z, по которым вычисляется разница .

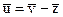2. Определяются оценки дисперсии 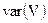и var(Z), на основе которых проводится расчет параметра 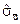(см. комментарий к формуле (5.57)).

3. На основании (5.57) создается статистика q, которая сравнивается с процентилями 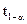. В случае, если 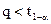, делают вывод про отсутствие ЦВЗ в изображении. В противном случае с вероятностью 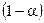ЦВЗ в изображении присутствует.

Рассмотрим возможный пример реализации данного метода в программе MathCAD.

Шаг1

Пусть изображение-контейнер представляет собой графический файл С.bmp (см. рис. 5.35, С). С := READBMP(C."bmp") При этом X := rows(C), Х= 128; Y = cols(C),Y=128

Черно-белое (двоичное) изображение ЦВЗ представлено на рис. 5.57: W=READBMP("W.bmp"), rows(W) = 128; cols(W) = 128

Количество нулевых и значащих элементов ЦВЗ одинаковое, исходя из чего среднее значение множества W:mean(W)=0,5.

Рис. 5.57. ЦВЗ, подлежащий внедрению в контейнер

Шаг 2

С помощью программных модулей (М.98, а, б) делим множество С на два подмножества одинаковой мощности 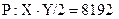в соответствии с формулами (5.53) и (5.54):

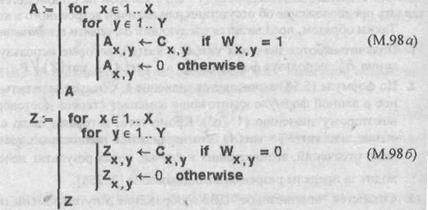
Графическая интерпретация результата разделения изображена на рис. 5.58.

Рис. 5.58. Графическая интерпретация подмножеств А и Z, а также их объединения A+Z

Шаг3

Используя программные модули (М.99, а, б) и (М.100, а ,б) определяем, соответственно, средние значения (mean)и дисперсии (var)подмножеств А и Z.

В результате имеем:

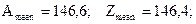
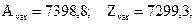
По полученным данным проводим расчет параметра:

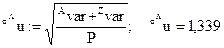
Шаг4

В соответствии с формулой 5.58 проводим вычисление значения k. Процентиль 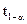получим исходя из того, что количество степеней свободы

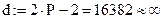
При этом

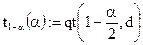
где 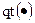— встроенная функция MathCAD расчета обратного кумулятивного распределения вероятностей (квантиля) для распределения Стьюдента. График зависимости 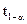приведен на рис. 5.59.

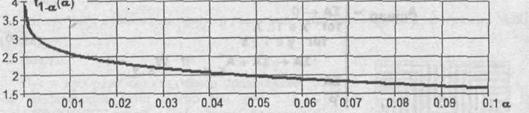
Рис. 5.59. Зависимость процентиля 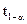от риска в допущении ошибки 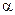.Задавшись значением 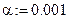, имеем 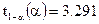, в результате чего

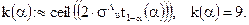
Шаг 5

В соответствии с (5.55) проводим встраивание ЦВЗ в подмножество А, изменяя элементы последнего на величину коэффициента k — программный модуль (М.101).

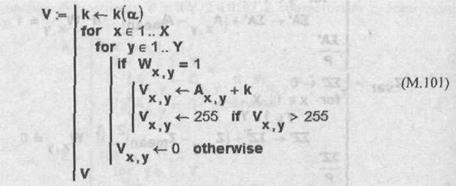
Использование в данном модуле оператора проверки условия 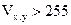позволяет предусмотреть возможность выхода значения элемента 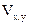из диапазона [0, 255]. Вид полученного подмножества V, а также "подписанное" изображение S := V+Z приведены на рис. 5.60

Рис. 5.60. Графическая интерпретация подмножества V и заполненного контейнера S

Шаг6

Для детектирования присутствия ЦВЗ в контейнере должны быть известны:

• изображение S*, подозреваемое на наличие встроенного ЦВЗ, и его размерность ;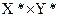

• изображение W*, которое, как предполагается, использовалось в качестве ЦВЗ.

Используя программные модули, аналогичные модулям (М.98, а,б), делим множество S* на подмножестваV* и Z* одинаковой мощности 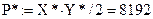, исходя из соответствующих значений элементов множества W*. Используя программные модули, подобные модулям (М.99) и (М.100), рассчитываем средние значения (mean)и дисперсии (var)полученных подмножеств:

.

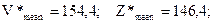
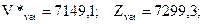По полученным данным находим значение параметров 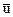и 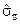(см. формулу (5.57)):

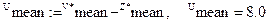
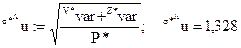
Таким образом, при 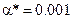, имеем:

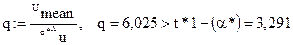
Из чего можно сделать вывод о том, что с вероятностью 99,9% в изображении S* присутствует ЦВЗ W*.

Структурные методы

Методы, получившие на сегодняшний день наибольшее распространение, в основном используют информационную избыточность на уровне пикселей (пространственная область) или же осуществляют преобразование в частотной области изображения. Ю.М. Коростиль и М.Е.Шелест предложили метод, в котором скрытие информации выполняется на содержательном уровне с использованием структурных и информационных параметров изображения [3,91]. Предложенный метод является развитием известной стеганографической технологии — семаграмм. Семаграммы представляют собой сообщения, в которых шифробозначеннями являются любые символы, кроме букв и цифр. Эти сообщения могут быть переданы, например, в рисунке, содержащем точки и тире для чтения по коду Морзе.

Суть же метода состоит в проведении последовательных преобразований отдельных фрагментов графического изображения, что в конечном итоге приводит к формированию скрываемого текста.

В структурных методах выделяют следующие этапы стеганопреобразования:

1. Преобразование защищаемого секретного сообщения М в цифровую форму D_M (например, с помощью любого криптографического кодирования), что подразумевает под собой шифрование текста со всеми соответствующими атрибутами.

2. Преобразование последовательности чисел D_M в графическую структуру G_M (граф, пиктограмму и т.п.), которая тем или иным способом может быть подвергнута формальному описанию.

3. Преобразование графической структуры G_M в визуальную информационную среду V_M (например, мультимедийную или же программную).

4. Использование совокупности методов и соответствующих процедур, с помощью которых формируется сюжет из визуальных образов со встроенными в них скрытыми сообщениями.

Следовательно, всю последовательность преобразований можно записать следующим образом:

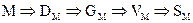
где 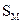– описание сюжета б который состоит из отдельных графических образов.