Среднеквадратическое (стандартное) отклонение (standard deviation)

Корень квадратный из значения дисперсии.

Стандартное отклонение выборки s_x вычисляют следующим образом:

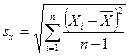
Мы делим на п -1 вместо n, поскольку генеральное среднее неизвестно, и вместо него ис­пользуют выборочное среднее, что делает выборку менее изменчивой, чем фактически. Деля на п —1вместо n, мы корректируем более слабую изменчивость значений переменой, наблюдае­мую в выборке. Для данных, приведенных в табл. 15.2, дисперсию вычисляют так:

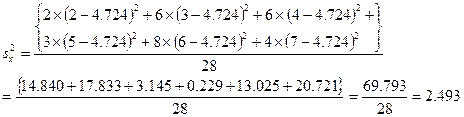
Следовательно, стандартное отклонение находим по формуле:

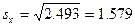
Коэффициент вариации(coefficient of variation) — это отношение стандартного отклонения к среднему арифметическому, выраженное в процентах. Коэффициент вариации — показатель относительной изменчивости переменной. Коэффициент вариации СVвычисляют так:

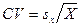
Коэффициент вариации (coefficient of variation)

Величина относительной изменчивости переменной, представляющая собой отношение ее стандартного отклонения к ее среднему значению.

Коэффициент вариации имеет смысл, только если переменную измеряют по относитель­ной шкале. Поскольку степень знакомства с Internet измерена не по этой шкале, то бессмыс­ленно вычислять коэффициент вариации для данных табл. 15.2.

Показатели формы распределения

Показатели формы распределения, как и показатели вариации, также полезны для понимания природы распределения переменной. Форму распределения оценивают с помощью асимметрии и эксцесса.

Асимметрия. Распределение переменной может быть симметричным или асимметричным (скошенным). При симметричном распределении частоты любых двух значений переменной которые расположены на одном и том же расстоянии от центра распределения, одинаковы. Равны между собой также и значения среднего арифметического, моды и медианы. Распределение асимметрично(skewness), если значения переменной, равноудаленные от среднего, имеют разную частоту, т.е. одна ветвь распределения вытянута больше другой (рис. 15.2). Значение асимметрии для распределения данных табл. 15.2 равно —0,094; что указывает на незначительную отрицательную асимметрию.

Симметричное распределение

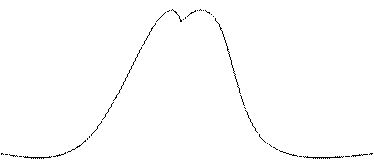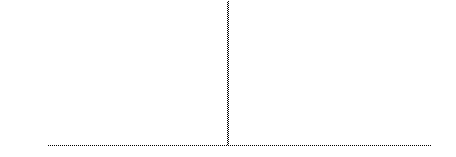
Среднее

Медиана

Мода

Асимметричное распределение

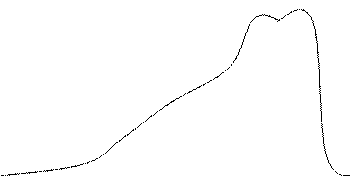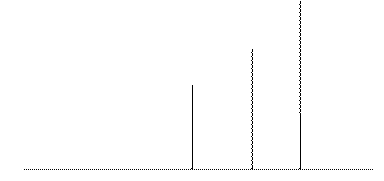
Среднее Медиана Мода

Рис. 15.2. Асимметрия распределения

Асимметрия (skewness)

Характеристика распределения, которая оценивает симметрию расположения значений данных относительно средней.

Эксцесс(kurtosis) — это показатель относительной крутости (островершинности или плосковершинности) кривой вариационного ряда по сравнению с нормальным распределением. Эксцесс нормально распределенной случайной величины равен нулю. Если эксцесс положителен, то распределение более островершинно по сравнению с нормальным распределением. При отрицательном значении распределение более плосковершинно по сравнению с нормальным. Значение этой статистики для табл. 15.2 равно—1,261; это указывает на то, что распределение более плосковершинное по сравнению с нормальным.

Эксцесс (kurtosis)

Мера относительной крутости кривой распределения частот.

ВВЕДЕНИЕ В ТЕОРИЮ ПРОВЕРКИ ГИПОТЕЗ

Этот раздел посвящен введению в теорию проверки гипотез. Базовый анализ данных неиз­менно включает в себя статистическую проверку гипотез. Приведем примеры гипотез в марке­тинговых исследованиях.

• Число постоянных покупателей универмага превышает 10% семей.

• Потребители определенной марки товара, которые отличаются между собой уровнем его потребления (много и мало), различаются также и психографическими характери­стиками.

• Рассматриваемый отель имеет более высокий имидж, чем его ближайший конкурент.

• Чем лучше респондент знаком с рестораном, тем чаще он его посещает.

В главе 12 мы рассмотрели понятия выборочного распределения, стандартную ошибку среднего и доли и доверительный интервал [6]. Все они относятся к проверке гипотезы и по­этому необходимо вспомнить их. Ниже мы опишем общую схему проверки гипотезы, которая применима к проверке гипотез с большим диапазоном параметров.