Встраивание путем модификации отношения между значениями коэффициентов в пределах одного блока 3 страница
 (5.46)
(5.46)
При произведении двух матриц "цена" вычисления одного элемента результирующей матрицы составляет N произведений и N суммирований, а при вычислении полной матрицы -  . Поскольку в (5.44), (5.46) присутствует по два произведения, вычисление матрицы
. Поскольку в (5.44), (5.46) присутствует по два произведения, вычисление матрицы 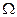 будет состоять из
будет состоять из  шагов:
шагов:
 (5.46)
(5.46)
По сравнению с (5.43) это существенное повышение скорости вычисления. Так, например, в случае  время вычисления сокращается приблизительно в 32 раза, при
время вычисления сокращается приблизительно в 32 раза, при  выигрыш составляет уже около 512.
выигрыш составляет уже около 512.
Программный модуль прямого ДКП трансформированных блоков изображения— (М.78):

График зависимости времени вычисления ДКП одного блока с помощью модуля (М.78) приведен на рис. S.48.

Рис. 5.48 Зависимости продолжительности ДКП блока от его размерности при использовании для вычисления программного модуля (М.78)
Шаг 5
Для удобства встраивания, развернем массив ЦВЗ в вектор, используя программный модуль (М.56). Очевидно, что общее количество элементов полученного вектора  будет равняться
будет равняться  ;
;  .
.
Шаг 6
Выбор НЧ-коэффициентов ДКП из матрицы 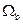 будем проводить исходя из того, что для элементов матрицы, которые находятся выше побочной диагонали (НЧ- коэффициенты), сумма индексов меньше чем N+1, а для тех, которые ниже (ВЧ-коэффициенты) — больше чем N+1.
будем проводить исходя из того, что для элементов матрицы, которые находятся выше побочной диагонали (НЧ- коэффициенты), сумма индексов меньше чем N+1, а для тех, которые ниже (ВЧ-коэффициенты) — больше чем N+1.
Введем метки L и Н, которые будут определять диапазон суммы индексов. Элемент матрицы 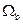 , сумма индексов которого не выходит за установленные пределы, будет выбираться для встраивания.
, сумма индексов которого не выходит за установленные пределы, будет выбираться для встраивания.
Программный модуль поиска метки Н при заданной метке L (M.79) построен на основе подсчета количества элементов, сумма индексов которых будет удовлетворять поставленному требованию невыхода за пределы диапазона (L, Н).

Верхний предел Н увеличивается до того момента, пока общее количество указанных элементов не превысит общего количества 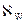 элементов вектора
элементов вектора  . Например, для
. Например, для  модуль (М.79) возвращает значение Н=62, что позволяет использовать для скрытия 1050 НЧ-коэффициентов каждой из матриц
модуль (М.79) возвращает значение Н=62, что позволяет использовать для скрытия 1050 НЧ-коэффициентов каждой из матриц 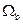 .
.
Встраивание ЦВЗ в выбранные НЧ-коэффициенты блоков изображения реализует программный модуль (М.80). В том случае, если индексная функция ind от абсолютного значения d НЧ-коэффициента отвечает j-му элементу вектора ЦВЗ  проводится поиск элементов прогрессии т, в интервале между которыми находится текущее значение d. Если данное значение является слишком близким к одной из границ интервала (а это, как указывалось выше, снижает стойкость создаваемой стеганосистемы), коэффициенту присваивается новое значение — первый член вектора элементов, распределенных, например, по нормальному закону при математическом ожидании
проводится поиск элементов прогрессии т, в интервале между которыми находится текущее значение d. Если данное значение является слишком близким к одной из границ интервала (а это, как указывалось выше, снижает стойкость создаваемой стеганосистемы), коэффициенту присваивается новое значение — первый член вектора элементов, распределенных, например, по нормальному закону при математическом ожидании  и стандартном отклонении
и стандартном отклонении  .
.
Указанное стандартное отклонение позволяет системе быть адаптированной к различным интервалам  , а также предотвратить случай, когда и новое значение коэффициента снова окажется близким к границе интервала. В свою очередь, выбор случайного числа из определенного интервала (а не, например, значения, которое отвечает середине интервала) делает невозможным образование подозрительных сосредоточений одинаковых значений коэффициентов ДКП.
, а также предотвратить случай, когда и новое значение коэффициента снова окажется близким к границе интервала. В свою очередь, выбор случайного числа из определенного интервала (а не, например, значения, которое отвечает середине интервала) делает невозможным образование подозрительных сосредоточений одинаковых значений коэффициентов ДКП.
Если индексная функция  коэффициенту присваивается случайное значение из ближайшего интервала —
коэффициенту присваивается случайное значение из ближайшего интервала —  , при
, при  ; и
; и  при
при  .
.
На рис. 5.49 cхематически изображены массивы ДКП четырех блоков изображения. При этом, темные шумоподобные диагональные полосы в верхних левых углах блоков отвечают модифицированном НЧ-коэффициентам, а светлые элементы массивов — не модифицированным.

Рис. 5.46. Массивы модифицированных (показано черным) НЧ-коэффицтктов ДКП
Шаг 7
Для реализации среднечастотного алгоритма Фридрих необходимо для каждого элемента ЦВЗ сгенерировать последовательность равномерно распределенных на интервале [0,1] ПСЧ.
В качестве основы генератора ПСЧ можно использовать ЛРСОС, реализованный программным модулем (M.57), который генерирует действительные числа, равномерно распределенные в интервале [1,2d]. Для получения ПСЧ, равномерно распределенных в интервале [0,1], достаточно разделить элементы полученного вектора  на значение максимального из них (2d), что и выполнено в программном модуле СМ.8П.
на значение максимального из них (2d), что и выполнено в программном модуле СМ.8П.

Модуль (М.81) позволяет сформировать для каждого из  символов ЦВЗ ПСП длиной 2d элементов. Начальное состояние (переменная start) генератора ПСЧ для 1-го символа ЦВЗ выбрано равным 74. В дальнейшем оно будет определяться значением элемента ПСП, который имеет индекс 74.
символов ЦВЗ ПСП длиной 2d элементов. Начальное состояние (переменная start) генератора ПСЧ для 1-го символа ЦВЗ выбрано равным 74. В дальнейшем оно будет определяться значением элемента ПСП, который имеет индекс 74.

В процессе исследования метода установлено, что алгоритм расширения спектра наиболее надежен, если отношение  . Поэтому предварительно принимаем
. Поэтому предварительно принимаем  . При этом 2d = 4096.
. При этом 2d = 4096.
Количество СЧ-коэффициентов ДКП блоков изображения, в которые будем встраивать ЦВЗ, примем равным  .
.
Элемент ЦВЗ, который равняется "+1", будем представлять случайным целым числом из диапазона [1,7]. а элемент, имеющий значение "-1" — случайным целым из диапазона [10,16].
С учетом заданных выше начальных данных, проведем выделение сегмента  , который будет представлять j-й символ ЦВЗ, для чего воспользуемся программным модулем (М.82), в котором парой функций
, который будет представлять j-й символ ЦВЗ, для чего воспользуемся программным модулем (М.82), в котором парой функций  осуществляется генерирование случайного по равномерному закону целого числа в одном из указанных выше диапазонов. С помощью функции
осуществляется генерирование случайного по равномерному закону целого числа в одном из указанных выше диапазонов. С помощью функции  выполняется выделение из вектора
выполняется выделение из вектора  сегмента длиной
сегмента длиной 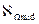 .
.

Разделим ЦВЗ на  частей, каждую из которых представим в виде отдельной суммы в (5.42). Данная процедура реализована программным модулем (М.83).
частей, каждую из которых представим в виде отдельной суммы в (5.42). Данная процедура реализована программным модулем (М.83).

Результатом выполнения (М.83) являются векторы  , элементы которых должны иметь гауссово распределение с нулевым математическим ожиданием и единичным стандартным отклонением. В нашем случае для каждого из блоков были получены следующие характеристики:
, элементы которых должны иметь гауссово распределение с нулевым математическим ожиданием и единичным стандартным отклонением. В нашем случае для каждого из блоков были получены следующие характеристики:
 |  | |
| 0.013 | 1.015 | |
| 0.002 | 0.973 | |
| -0.001 | 0.976 | |
| -0.012 | 0.991 |
Выбор из матрицы 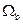 СЧ-коэффициентов будем проводить, исходя из того, что для элементов, которые формируют побочную диагональ матрицы, сумма интервалов равняется N+1, сама же диагональ состоит из N элементов.
СЧ-коэффициентов будем проводить, исходя из того, что для элементов, которые формируют побочную диагональ матрицы, сумма интервалов равняется N+1, сама же диагональ состоит из N элементов.
Введем метки L' и Н', определяющие диапазон суммы индексов, попадание в который будет относить рассматриваемый СЧ-коэффициент к разряду тех, в которые будет проводиться встраивание векторов  При
При  и N=128 в результате использования программного модуля (М.84) получены следующие результаты: L'=111, Н'=147, что делает доступными для встраивания 4174 СЧ-коэффициентов каждой из матриц
и N=128 в результате использования программного модуля (М.84) получены следующие результаты: L'=111, Н'=147, что делает доступными для встраивания 4174 СЧ-коэффициентов каждой из матриц 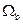

Встраивание элементов векторов  выбранные СЧ-коэффициенты блоков контейнера выполняет программный модуль (M.85).
выбранные СЧ-коэффициенты блоков контейнера выполняет программный модуль (M.85).

Схематическое изображение результата встраивания (как отличия от оригинальных матриц 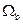 ) приведено на рис. 5.50.
) приведено на рис. 5.50.
Шаг 9
К модифицированным матрицам  применим операцию обратного ДКП (модуль (М.86)) и на основе воссозданный блоков формируем общий массив контейнера (модуль (М.87)).
применим операцию обратного ДКП (модуль (М.86)) и на основе воссозданный блоков формируем общий массив контейнера (модуль (М.87)).

Рис. 5.50. Массивы модифицированных (изображено черным) НЧ и СЧ-коэффициентов ДКП

Контейнер со встроенным ЦВЗ изображен на рис. 5.51.
Шаг 10
При извлечении ЦВЗ контейнер  предварительно разбивается на блоки размерностью
предварительно разбивается на блоки размерностью  ,
,  , общим количеством
, общим количеством  — модуль (М.55) с соответствующей подстановкой указанных переменных.
— модуль (М.55) с соответствующей подстановкой указанных переменных.
Для каждого блока выполняется трансформация (5.37), для чего используется программный модуль, подобный модулю (М.75). Для параметра  формируется прогрессия
формируется прогрессия  и определяется индексная функция
и определяется индексная функция  .
.

Рис. 6.51. Изображение со встроенным ЦВЗ при параметрах 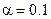 и
и 
Выполняется операция прямого ДКП трансформированных блоков изображения (модуль (М.78)).
Для извлечения скрытых данных из матриц ДКП предварительно должны быть заданными (либо вычисленными по заранее оговоренным с передающей стороной алгоритмам) следующие параметры:  ,
,  ;
;  ,
,  ,
,  ,
,  ,
,  . Программный модуль извлечения — (М.88).
. Программный модуль извлечения — (М.88).
Первым циклом перебирания индексов блоков контейнера из полученных матриц ДКП выбираются те НЧ-коэффициенты, в которые было произведено встраивание данных. Указанные коэффициенты выступают в роли аргументов индексной функции, формируя вектор low. Полученный для каждого блока результат вычисления заносится в b-ый элемент массива 
Следующим циклом перебирания индексов блоков из матриц ДКП выбираются модифицированные СЧ-коэффициенты, которые формируют вектор mid. Владея предварительной информацией о том, что ЦВЗ был разделен поровну между блоками, а элементы ЦВЗ представлены целыми числами от 1 до 16, из элемента массива 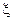 , который имеет индекс
, который имеет индекс  , выделяются все 16 сегментов длиной по
, выделяются все 16 сегментов длиной по  элементов.
элементов.
Для каждого из этих сегментов вычисляется взаимная корреляционная функция с вектором mid выделенных СЧ-коэффициентов. Проводится поиск индекса, который отвечает наибольшему значению корреляции. Если значение этого индекса меньше или больше 8, делается вывод о том, что встроенный элемент ЦВЗ имел значение, соответственно, +1 или -1, которое и присваивается элементу вектора V.
Указанный вектор имеет размерность  и формируется отдельно для каждого блока, образовывая впоследствии
и формируется отдельно для каждого блока, образовывая впоследствии  -й элемент массива
-й элемент массива  .
.
Таким образом, результирующий массив  состоит из 5 элементов, каждый из которых, в свою очередь, является вектором размерностью
состоит из 5 элементов, каждый из которых, в свою очередь, является вектором размерностью  . Элементы массива
. Элементы массива  , по сути, представляют собой 5 гипотез относительно возможного вида ЦВЗ, которые в идеале должны быть идентичными. Для формирования единственной гипотезы используется "принцип большинства": j-му элементу результирующего вектора
, по сути, представляют собой 5 гипотез относительно возможного вида ЦВЗ, которые в идеале должны быть идентичными. Для формирования единственной гипотезы используется "принцип большинства": j-му элементу результирующего вектора  присваивается такое значение, которое преобладает среди всех 5 элементов, имеющих индексj.
присваивается такое значение, которое преобладает среди всех 5 элементов, имеющих индексj.

Для случая, рассмотренного в модуле (М.88), из этих 5 элементов формируется вектор  , для которого подсчитывается среднее значение. Если последнее окажется положительным (количество единиц преобладает), то элемент
, для которого подсчитывается среднее значение. Если последнее окажется положительным (количество единиц преобладает), то элемент  . В противном случае,
. В противном случае, 
Полученный вектор  сворачивается в массив
сворачивается в массив  с размерностью оригинального ЦВЗ (за основу можно использовать программный модуль (М.74)).
с размерностью оригинального ЦВЗ (за основу можно использовать программный модуль (М.74)).
На рис. 5.52 представлен ЦВЗ, извлеченный из контейнера, который предварительно был подвергнут JPEG-компрессии. В первых двух случаях очевидно полное соответствие извлеченного ЦВЗ оригиналу. Количество ошибочно распознанных элементов ЦВЗ в третьем случае составило 3 пикселя (или 0,29% от общего их количества  ); для г) — 58 (5,66%); для д) — 109 (10,64%); для е) — 194 (18,95%).
); для г) — 58 (5,66%); для д) — 109 (10,64%); для е) — 194 (18,95%).

Рис. 5.52. ЦВЗ (увеличено), извлеченные из контейнера S* ( 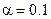 ,
,  ) формат S* не изменен (а); применена JPEG-компрессия с сохранением 100% качества изображения (б); то же при сохранении 75, 50, 25 и 0% качества (соответственно: в, г, д, е)
) формат S* не изменен (а); применена JPEG-компрессия с сохранением 100% качества изображения (б); то же при сохранении 75, 50, 25 и 0% качества (соответственно: в, г, д, е)
Увеличение параметров 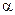 и, особенно,
и, особенно, 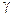 делает данную стеганосистему еще более устойчивой к атаке компрессией, однако при этом сильно страдает качество изображения.
делает данную стеганосистему еще более устойчивой к атаке компрессией, однако при этом сильно страдает качество изображения.
Результаты вычисления показателей визуального искажения контейнера при значениях параметров  ,
,  внесены в табл. 5.4. При этом следует иметь в виду, что объем изображения-контейнера был увеличен в четыре раза, по сравнению с контейнерами, используемыми при рассмотрении предыдущих методов.
внесены в табл. 5.4. При этом следует иметь в виду, что объем изображения-контейнера был увеличен в четыре раза, по сравнению с контейнерами, используемыми при рассмотрении предыдущих методов.
Таблица 5.4 Показатели визуального искажения в случае скрытия данных в частотной области изображения
| Название показателя искажения | Оригинал | Методы скрытия в частотной области | ||||||||
| Коха-Жао (Р=0.5) | Коха-Жао (Р=25) | Бенгама-Мемона (Р=1) | Бенгама-Мемона (Р=35) | Хсу-Ву (а) | Хсу-Ву (б) | Фридрих (α=0.1, γ=1) | Фридрих (α=0.1, γ=2) | Фридрих (α=0.2, γ=1) | ||
| Максимальная разность MD | ||||||||||
| Средняя абсолютная разность AD | 9.504 | 11.392 | 1.846 | 3.042 | 36.805 | 26.457 | 19.233 | 25.990 | 22.413 | |
| Нормированная абсолютная разность NAD | 0.074 | 0.088 | 0.014 | 0.024 | 0.251 | 0.181 | 0.131 | 0.179 | 0.154 | |
| Средне- квадратическая ошибка MSE | 124.383 | 178.342 | 15.427 | 31.417 | 1794.673 | 962.154 | 543.072 | 942.113 | 718.449 | |
| Нормированная средне- квадратическая ошибка NMSE | 5.065·10-3 | 7.263·10-3 | 6.283·10-4 | 1.279·10-3 | 0.062 | 0.033 | 0.019 | 0.033 | 0.025 | |
| Lp- норма, р=2 | 11.153 | 13.354 | 3.928 | 5.605 | 42.364 | 31.019 | 23.304 | 30.694 | 26.804 | |
| Лапласова средне квадратическая ошибка, LMSE | 0.020 | 0.037 | 0.027 | 0.053 | 0.444 | 0.297 | 0.352 | 1.010 | 0.362 | |
| Отношение сигнал/шум, SNR | ∞ | 197.423 | 137.690 | 1.592·103 | 781.605 | 16.056 | 29.948 | 52.178 | 30.078 | 39.441 |
| Максимальное отношение сигнал/шум PSNR | ∞ | 522.782 | 364.608 | 4.215·103 | 2.070·103 | 36.232 | 67.583 | 119.735 | 69.020 | 90.507 |
| Качество изображения IF | 0.994935 | 0.992737 | 0.999372 | 0.998721 | 0.937717 | 0.966609 | 0.980835 | 0.966753 | 0.876281 | |
| Нормированная взаимная корреляция NC | 0.993261 | 0.986178 | 0.996790 | 0.994154 | 0.788233 | 0.863134 | 0.903486 | 0.873017 | 0.876281 | |
| Качество корреляции CQ | 190.182 | 188.901 | 187.554 | 189.572 | 189.071 | 155.023 | 169.754 | 176.042 | 170.106 | 170.742 |
| Структурное содержание SC | 1.008484 | 1.020804 | 1.005826 | 1.010523 | 1.565560 | 1.316381 | 1.210451 | 1.283235 | 1.285458 | |
| Общее сигма-отношение сигнал/шум GSSNR | ∞ | 87.792 | 60.244 | 4.388·103 | 2.167·103 | 6.326 | 74.183 | 18.153 | 10.080 | 13.899 |
| Сигма-отношение сигнал/шум SSNR | ∞ | 72.9 | 67.3 | 73.3 | 69.2 | 30.1 | 40.8 | 198.8 | 158.1 | 179.8 |
| Нормированное отношение сигнал/шум NSER | ||||||||||
| Подобие гистограмм HS |
Методы расширения спектра
Изначально методы расширения спектра (PC или SS — Spread-Spectrum) использовались при разработке военных систем управления и связи. Во время второй мировой войны расширение спектра использовалось в радиолокации для борьбы с намеренными помехами. В последние годы развитие данной технологии объясняется желанием создать эффективные системы радиосвязи для обеспечения высокой помехоустойчивости при передаче узкополосных сигналов по каналам с шумами и осложнения их перехвата. Система связи является системой с расширенным спектром в следующих случаях [65].
• Полоса частот, которая используется при передаче, значительно шире минимально необходимой для передачи текущей информации. При этом энергия ин формационного сигнала расширяется на всю ширину полосы частот при низком соотношении сигнал/шум, в результате чего сигнал трудно обнаружить, пере хватить или воспрепятствовать его передаче путем внесения помех. Хотя суммарная мощность сигнала может быть большой, соотношение сигнал/шум в любом диапазоне частот является малым, что делает сигнал с расширенным спектром трудно определяемым при радиосвязи и, в контексте скрытия информации стеганографическими методами, трудно различимым человеком.
• Расширение спектра выполняется с помощью так называемого расширяющего (или кодового) сигнала, который не зависит от передаваемой информации. Присутствие энергии сигнала во всех частотных диапазонах делает радиосигнал с расширенным спектром стойким к внесению помех, а информацию, встроенную в контейнер методом расширения спектра, стойкой к ее устранению или извлечению из контейнера. Компрессия и другие виды атак на систему связи могут устранить энергию сигнала из некоторых участков спектра, но поскольку последняя была распространена по всему диапазону, в других полосах остается достаточное количество данных для восстановления информации. В результате, если, разумеется, не разглашать ключ, который использовался для генерации кодового сигнала, вероятность извлечения информации неавторизованными лицами существенно снижается.
• Восстановление первичной информации (то есть "сужение спектра") осуществляется путем сопоставления полученного сигнала и синхронизированной копии кодового сигнала.
В радиосвязи применяют три основных способа расширения спектра:
• с помощью прямой ПСП (РСПП);
• с помощью скачкообразного перестраивания частот;
• с помощью компрессии с использованием линейной частотной модуляции(ЛЧМ).
При расширении спектра прямой последовательностью информационный сигнал модулируется функцией, которая принимает псевдослучайные значения в установленных пределах, и умножается на времени константу — частоту (скорость) следования элементарных посылок (элементов сигнала). Данный псевдослучайный сигнал содержит составляющие на всех частотах, которые, при их расширении, модулируют энергию сигнала в широком диапазоне.
В методе расширения спектра с помощью скачкообразного перестраивания частот передатчик мгновенно изменяет одну частоту несущего сигнала на другую. Секретным ключом при этом является псевдослучайный закон изменения частот.
При компрессии с использованием ЛЧМ сигнал модулируется функцией, частота которой изменяется во времени.
Очевидно, что любой из указанных методов может быть распространен на использование в пространственной области при построении стеганографических систем.
Рассмотрим один из вариантов реализации метода РСПП, авторами которого являются Смит (J.R. Smith) и Комиски (В.О. Comiskey) [88]. Алгоритм модуляции следующий: каждый бит сообщения  , представляется некоторой базисной функцией
, представляется некоторой базисной функцией  , размерностью
, размерностью  , умноженной, в зависимости от значения бита (1 или 0), на +1 или -1:
, умноженной, в зависимости от значения бита (1 или 0), на +1 или -1:
