Краткие теоретические сведения. 2.1.1. Основные виды теплообмена: теплопроводность, конвективный теплообмен

2.1.1. Основные виды теплообмена: теплопроводность, конвективный теплообмен, теплообмен излучением

Теплообмен это – сложный процесс, который можно представить как совокупность отдельных простых процессов. Различают три элементарных вида теплообмена – теплопроводность, конвенцию и тепловое излучение.

Количество переносимой в единицу времени теплоты при теплообмене называется тепловым потоком Q, Вт. Тепловой поток, проходящий через единицу площади поверхности F, м², перпендикулярной к направлению потока, называется удельным тепловым потоком q, Вт/м²

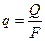. (2.1)

В процессе теплопроводности обмен энергии происходит при непосредственном соприкосновении частиц вещества (молекул, атомов и свободных электролитов) при их тепловом движении. Основным законом теплопроводности является закон Фурье, установивший прямую пропорциональную зависимость между удельным тепловым потоком и температурным градиентом:

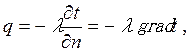
(2.2)

где l - множитель пропорциональности, который называется коэффициентом теплопроводности, Вт/(м·°С). Коэффициент теплопроводности численно равен удельному тепловому потоку при температурном градиенте, равном единице, т.е. при уменьшении температуры на 1°С на единицу длины.

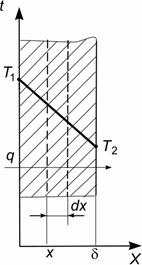
Рассмотрим процесс теплопроводности через плоскую однослойную стенку толщиной d при стационарном режиме (рисунок. 2.1). Коэффициент теплопроводности материала стенки постоянен и равен l. Температура на поверхностях стенки Т₁ и Т₂, причем Т₁ > Т₂. Температура изменяется только в направлении оси Х, перпендикулярной поверхности стенки.

Величина удельного теплового потока через плоскую стенку определяется из выражения:

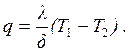(2.3)

Уравнение (2.5) можно представить в виде:

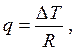(2.4)

где R = 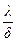— термическое сопротивление
теплопроводности стенки, (м²К)/Вт.

Если стенка состоит из нескольких слоев, то
ее термическое сопротивление определяется по
формуле

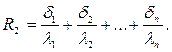(2.5)

Определив величину удельного теплового потока q, можно вычислить общее количество теплоты Q, Вт, передаваемой через стенку площадью F, м², по формуле:

Q = qF. (2.6)

Температуры в любом сечении стенки х можно определить по формуле:

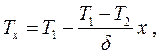(2.7)

которая является приближенной, так как коэффициент теплопроводности l. В общем случае зависит от температуры и температура стенки в действительности изменяется по криволинейному закону.

Процесс конвенции происходит исключительно в жидкостях и газах и представляет собой перенос теплоты за счет перемещения и перемешивания отдельных частиц жидкости или газа. Конвенция всегда сопровождается теплопроводностью. Различают процессы естественной и вынужденной конвенции. В процессе естественной конвенции перемещение частиц жидкости или газа происходит за счет разности плотностей отдельных объемов вещества. Если перемещение жидкости или газа происходит за счет воздействия какого-либо побудителя движения (насоса, вентилятора и др.), то перенос теплоты при этом называют вынужденной конвенцией. Процесс теплообмена в этом случае происходит значительно интенсивней, чем при естественной конвенции.

Тепловой поток Q, Вт, при конвективном теплообмене определяется по формуле Ньютона

Q = aF(t_ж – Т), (2.8)

где a – коэффициент пропорциональности, называемый коэффициентом теплоотдачи, Вт/(м²·°С); t_ж – температура жидкости, °С; Т – температура поверхности тела, °С; F – площадь поверхности теплообмена, м². Если принять F = l м², получим величину удельного теплового потока (плотность теплового потока) q, Вт/м²

q = a(t_ж – Т), (2.9)

Коэффициент теплоотдачи определяет количество теплоты, в Дж, передаваемой за 1 с от жидкости к поверхности тела (или наоборот) через 1 м² при разности температур жидкости и поверхности в 1К. На величину коэффициента теплоотдачи а влияют множество факторов: форма Ф, размеры l и температура t_с поверхности, скорость жидкости w, ее температура t_ж, физические свойства жидкости, описываемые через коэффициент теплопроводности l, коэффициент динамической вязкости μ, плотность ρ, теплоемкость с_p , температурный коэффициент объемного расширения b и др. Таким образом,

a = f(Ф, Т, w, t_ж, l, μ, r, с_p, b…). (2.10)

Для определения величины a, необходимой для решения практических задач, используют данные, полученные экспериментальным путем, представленные с использованием «критериев подобия», а именно безразмерных комплексов, составленных из величин, характеризующих изучаемый процесс.

Основные критерии подобия, используемые при определении величины a:

Nu = al/l – критерий Нуссельта, характеризующий относительную интенсивность теплоотдачи на границе жидкость (газ) – твердое тело и всегда являющийся величиной искомой.

Re = rwl/μ = wl/v – критерий Рейнольдса, представляющий собой отношение сил инерции к силам внутреннего трения и характеризующий гидродинамический режим движения жидкости. v = μ/r - коэффициент кинематической вязкости.

Pr = μс_pg/l – критерий Прандтля, характеризующий физические свойства жидкости (газа). G – ускорение свободного падения.

Gr = glb∆t/n² – критерий Гросгофа, характеризующий соотношением подъемных сил, возникающих в жидкости (газе) вследствие разности плотностей в рассматриваемом объеме, обусловливающей естественную конвенцию и силой инерции.

В общем случае конвективного теплообмена критериальная зависимость имеет вид

Nu_x = f(Re_x, Gr_x, Pr_x). (2.11)

Критерии Re_x, Gr_x, Pr_x в этом выражении являются определяющими критериями. Индекс х – указывает, что они вычислены при определенных условиях.

Теплообмен в условиях вынужденного турбулентного движения
оценивается критериальным уравнением вида

Nu = cReⁿ Pr^m. (2.12)

где с, n, m - соответственно коэффициент и показатели степени, определяемые экспериментально. Они приведены в справочной литературе.

В режиме естественной конвенции теплоотдача в критериальном виде может быть описана общей степенной зависимостью вида

Nu = c(Gr Pr)ⁿ, (2.13)

где c, n - экспериментально определяемые величины, которые различают для отдельных диапазонов аргумента (Gr Pr).

Тепловое излучение – это процесс переноса теплоты от одного тела к другому электромагнитными волнами, возникающими в результате сложных молекулярных и атомных возмущений.

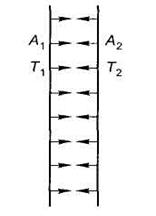В самом простом случае величина теплового потока между двумя параллельными стенками (рисунок 2.2) определяется по уравнению

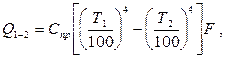(2.14)

где С_пр – приведенный коэффициент излучения, Вт/(м²×К);

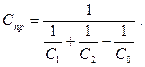(2.15)

Здесь С₁ и С₂ – коэффициенты излучения тел, определяемые по формуле:

С = eС₀, (2.16)

где e - отношение энергии излучения серого тела к энергии излучения абсолютно черного тела при одинаковой температуре, явля­ется характеристикой серого тела, называется относительной излучательной способностью или степенью черноты тела, значения приведены в справочной литературе для различных материалов и качества поверхности тел;

С₀ - коэффициент излучения абсолютно черного тела, равный 5,68 Вт/(м² К⁴).

Уравнение (2.14) справедливо для расчета лучистого теплообмена между телами, меньшее из которых является выпуклым и окружено поверхностью другого, т.е. находится в замкнутом пространстве (рисунок 2.3).

При этом

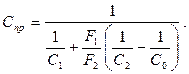(2.17)

где F₁ и F₂ – площади поверхности тел, между которыми происходит процесс лучистого теплообмена.

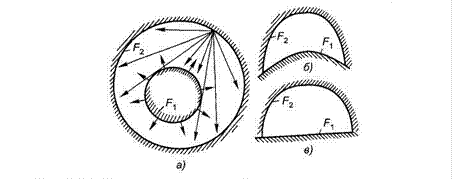
Рисунок 2.3 - Схема лучистого теплообмена в замкнутом пространстве

В формуле (2.17) во всех случаях в качестве расчетной при принимается меньшая из поверхностей.

2.1.2. Основные законы и расчетные уравнения теплопередачи

На практике часто встречающимся случаем является теплообмен между двумя жидкостями (жидкостью и газом) через разделяющую стенку. Это еще более сложный процесс, в котором сочетаются действия рассмотренных элементарных процессов. Такой процесс называется теплопередачей. Количественной характеристикой этого процесса является коэффициент тепло передачи К, величина которого равна удельному тепловому потоку q, Вт/м², переданному от одного жидкости к другой при разности температур между ними в один градус.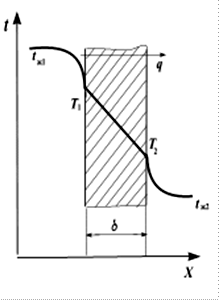

Пусть имеется плоская однослойная стенка толщиной δ с коэффициентом теплопроводности l.

По одну сторону стенки находится горячая среда с температурой t_ж1, по другую – холодная среда с температурой t_ж2. Неизвестные температуры поверхностей стенок обозначим соответственно Т₁ и Т₂ (рисунок 2.4). Тепловой поток направлен от горячей среды к холодной.

Процесс теплопередачи состоит из трех этапов: теплоотдача от горячей среды (жидкости или газа) к поверхности стенки, теплопроводность через стенку и теплоотдача от противоположной поверхности стенки к холодной середе. Значение коэффициентов теплоотдачи определяются условиями состояния и движения горячей и холодной сред и соответственно равны a₁ и a₂.

Величина удельного теплового потока q, Вт/м², определяется по формуле:

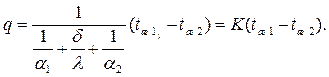(2.18)

Таким образом, чтобы вычислить значение коэффициента теплопередачи K для плоской стенки, необходимо знать толщину d и коэффициент теплопроводности l стенки, а также коэффициенты теплоотдачи a₁ и a₂. Величина, обратная коэффициенту теплопередачи, называется термическим сопротивлением теплопередаче и обозначается R, м²×К/Вт.

Из уравнения (2.18) имеем:

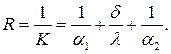(2.19)

Из последнего выражения следует, что общее термическое сопротивление равно сумме частных. Поэтому если стенка многослойная, то ее термическое сопротивление равно

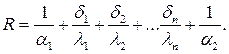
или

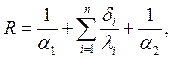(2.20)

где d₁, d₂, ... d_n – толщина слоев, м;

l₁, l₂, ... l_n – коэффициенты их теплопроводности, Вт/(м×К).

Температуры поверхностей стенк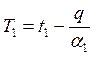и:

и 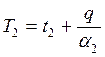. (2.21)

Примеры и задачи

2.2.1. Основные виды теплообмена

Пример 1: Определить тепловой поток через бетонную стенку гаража толщиной d = 0,2 м, высотой Н = 2,5 м и длиной L = 2 м, если температуры на ее поверхностях Т₁ = 20^oC и Т₂ = (-10)^oC, а коэффициент теплопроводности l = 1,0Вт/(м×К).

Решение:

Тепловой поток

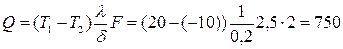Вт,

где 2,5×2 м² – площадь стенки F.

Пример 2.Во сколько раз уменьшаться тепловые потери через стенку гаража, если между двумя слоями кирпичей толщиной d_к = 0,25 м, установить прокладку из пенопласта толщиной d_п = 0,05 м. Коэффициенты теплопроводности кирпичной кладки и пенопласта, соответственно, равны l_к = 0,5 Вт/(м×К) и l_п = 0,05 Вт/(м×К).

Решение:

Коэффициент термического сопротивления двух слоев кирпичной кладки

.

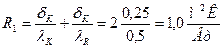Коэффициент термического сопротивления двух слоев кирпичной кладки с прокладкой из пенопласта:

.

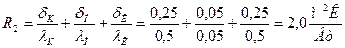Т.о., тепловые потери через стенку гаража уменьшаться в два раза.

Пример 3. Какую минимальную тепловую мощность Q_min , кВт, должен иметь встроенный в цистерну подогреватель нефтепродукта, чтобы обеспечить среднюю температуру поверхности цистерны Т =52°С? Котел цистерны диаметром d = 2,8 м, имеющий расчетную площадь поверхности F = 110м2 , расположен горизонтально и защищен от ветра. Температура воздуха — t_ж = 15°С. Для определения среднего коэффициента теплоотдачи от поверхности цистерны воспользоваться эмпирической формулой для расчета теплообмена около горизонтальной трубы в условиях естественной конвекции: 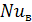= 0,47*( .

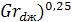Физические характеристики воздуха при температуре 15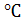

Коэффициент теплопроводности 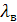= 0,0255 Вт/(м*К)

Кинематическая вязкость 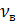= 1,461*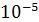 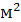/с

Критерий Прандтля 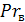= 0,704

Коэффициент температурного расширения воздуха 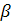=1/(273+ t_ж) =
0,0035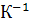

Решение:

1. Определим критерии Грасгофа при свободном поперечном обтекании горизонтальной трубы воздухом

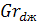= 9,81* 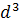* *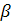(Т -t_ж )/n²= 9,81* 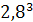*0,0035*(52 -15)/(1,461* 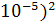= 1306,51* .

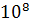2. Определим критерий Нуссельта по эмпирической формуле

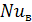= 0,47*( 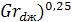= 0,47*(1306,51* 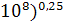= 282,57.

3. Определим коэффициент теплоотдачи от цистерны к воздуху

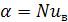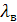* /d = 282,57*0,0255/2,8 = 2,573 Вт/( 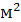*К).

4. Определим потери теплоты цистерной

Q = 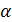*F*( Т -t_ж ) = 2,573*110*(52-15) = 10472 Вт=10,5 кВт

Поскольку потери тепла компенсируются встроенным в цистерну подогревателем нефтепродукта, то: 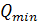= = 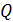10,5 кВт.

Пример 4:Рассчитать конвективный коэффициент теплоотдачи и определить конвективный тепловой поток от стенки трубы подогревателя, если внутренний диаметр трубы d_н = 0,016 м, длина трубы l = 2 м, температура стенки трубы Т = 100^oC, температура воды t_ж = 40^oC, скорость течения воды в трубе w = 0,995 м/с.

Теплофизические свойства воды при температуре t_ж = 40^oC: теплопроводность l_ж = 0,634 Вт/(м×К), коэффициент кинематической вязкости n_ж = 0,659×10^-6 м²/с, число Прандтля Pr_ж = 4,3.

Для определения среднего коэффициента теплоотдачи от поверхности трубы воспользоваться эмпирической формулой для расчета теплообмена от трубы в условиях вынужденной конвекции: Nu_ж = 0,021*Re_ж^0,8Pr_ж^0,43(Pr_ж/ Pr_с)^0,25.

Число Прандтля при температуре t_с = 100^oC равно Pr_жс = 1,75.

Решение:

1. Определим критерий Рейнольдса при вынужденном обтекании трубы водой

Re_ж = w*d/n_ж = 0,955*0,016 / 0,659×10^-6 = 2,42×10^-4.

2. Определим критерий Нуссельта по эмпирической формуле

Nu_ж = 0,021*Re_ж^0,8Pr_ж^0,43(Pr_ж/ Pr_с)^0,25 = 0,021*(2,42×10^-4)^0,8* 4,3^0,43(4,3 / 1,75)^0,25 = 158.

3. Определим коэффициент теплоотдачи от цистерны к воздуху

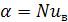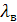* /d = 158*0,634/0,016 = 6260 Вт/( 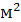*К).

4. Определим конвективный тепловой поток от стенки трубы к воде

Q = 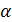*F*( Т -t_ж ) = 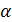*p*d*l*( Т -t_ж ) 6260*3,14*0,016*2*(100 - 40)
= 37,8 ×10³ Вт.

Пример 5: Рассчитать тепловой поток от стальных окисленных труб с наружным диаметром d_н = 0,1 м, общей длиной l = 2 м,используемых для отопления гаража, с температурой стен t₂= 15 ^оС .

Температура стенок труб t₁= 85 ^оС

Степень черноты стенок труб e = 0,8.

Решение:

1. Определим площадь теплоотдающей поверхности

F = p*d*l = 3,14*0,1*10 = 3,14 м².

2. Определим приведенный коэффициент излучения. Поскольку площадь стен во много раз более площади труб, т.е. F₂ >> F₁, отношение F₁ / F₂ в формуле (2.15) обращается в ноль.

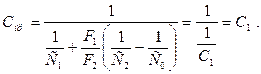
Поскольку известна степень черноты труб С_пр = С₁ = e*С₀ = 0,8*5,67
4,536 Вт/(м²К⁴).

3. Рассчитаем тепловой поток

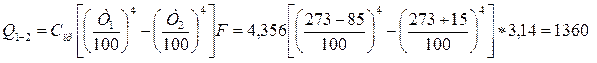Вт.

Задачи для самостоятельного решения:

1. Определить тепловой поток через двухслойную стену склада из бетона толщиной d_к = 0,15 м, и слоя пенопласта толщиной d_п = 0,1 м. Коэффициенты теплопроводности бетонной плиты и пенопласта, соответственно, равны l_б = 1,0Вт/(м×К) и l_п = 0,05 Вт/(м×К) высотой Н = 3 м и длиной L = 5 м, если температуры на ее поверхностях Т₁ = 20^oC и Т₂ = (-20)^oC.

2. Для отопления гаража используют трубу, в которой протекает горячая вода. Рассчитать конвективный коэффициент теплоотдачи и конвективный тепловой поток, если наружный диаметр трубы d_н = 0,1 м, длина трубы l = 10 м, температура стенки трубы t_c = 80^oC, температура воздуха в гараже t_ж = 20^oC.

Теплофизические свойства воздуха при температуре t_ж = 20^oC: теплопроводность l_ж = 2,59×10^-2 Вт/(м×К), коэффициент кинематической вязкости n_ж = 15,06×10^-6 м²/с, число Прандтля Pr_ж = 0,703, коэффициент расширения b_ж = 1/Т_ж = 1/(273+20) = 3,4×10^-3 1/К.

Число Прандтля при температуре t_с = 85^oC равно Pr_с = 0,691.

3. Температура поверхности вертикальной стенки высотой h=3м равна t_с=10°С. Температура воздуха в помещении t_ж=20°С. Определить коэффициент теплоотдачи от воздуха к стенке.

Теплофизические свойства воздуха при температуре t_ж = 20^oC:

теплопроводность l_ж = 2,59×10^-2 Вт/(м×К), коэффициент кинематической вязкости n_ж = 15,06×10^-6 м²/с, число Прандтля Pr_ж = 0,703, коэффициент расширения b_ж = 1/Т_ж = 1/(273+20) = 3,4×10^-3 1/К.

Число Прандтля при температуре t_с = 10^oC равно Pr_с = 0,705.

4.Рассчитать лучистый тепловой поток от стальной окисленной трубы (степень черноты ε₁=0,8), используемой для отопления гаража, если наружный диаметр трубы d_н = 0,1м, длина трубы l = 10 м, температура стенки трубы t₁ = 85^oC, температура стен гаража t₂ = 15^oC.

2.2.2. Расчеты процессов теплопередачи

Пример: Тепло от дымовых газов передается через плоскую стенку кипящей воде. Температура газов t_ж1, воды – t_ж2 ,суммарный коэффициент теплоотдачи от газов к стенке α₁ , а от стенки к воде – α₂ . Стенка стальная, чистая (λ₁=50,1 Вт/(м К)) толщиной δ₁. Рассчитать коэффициент теплопередачи К. Как измениться коэффициент теплопередачи к, если:

1. Стальную стенку заменить медной, толщиной 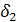,( 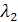=392 Вт/(м К))

2. На стальной стенке со стороны воды образовалась накипь, толщиной 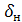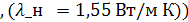, а со стороны газа - слой сажи, толщиной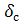 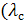=0,87 Вт/(м К))

Определить также термические сопротивления, плотность теплового потока, температуры на границе слоев.

t_ж1=1200 ^оС, t_ж2=100 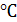, 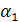=90 Вт/( 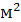К), 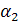=3000 Вт/( 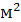К), 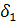=10 мм, 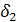=8 мм, 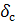=1 мм, 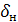=3 мм.

Решение:

Определим коэффициент теплопередачи для чистой стальной стенки

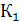=1/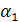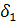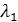(1/ + / +1/ 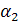)=85,88 Вт/( 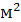К)

Определим коэффициент теплопередачи для чистой медной стенки

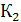=1/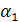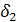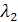(1/ + / +1/ 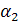)=87,22 Вт/( 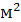К)

Определим коэффициент теплопередачи для стальной стенки, после ее эксплуатации

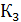=1/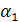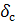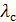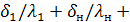(1/ + / + 1/ 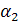)=39,88 Вт/( 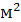К)

При замене стальной стенки на медную коэффициент теплопередачи увеличился на

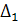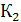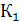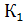=(( - )/ )100%=1,6%

После эксплуатации стальной стенки коэффициент теплопередачи уменьшился в

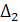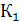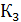= / =2,15 раза

Определим плотность теплового потока до эксплуатации

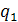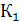= х(t_ж1- t_ж2)=94468 Вт/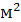

Определим плотность теплового потока поcле эксплуатации

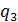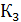= х(t_ж1- t_ж2)=43870 Вт/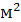

Определим плотность теплового потока через чистую медную стенку

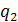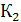= х(t_ж1- t_ж2)=95942 Вт/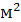

Определим термические сопротивления слоев стенки после ее эксплуатации

Слой сажи 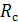= =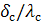0,0115 (К 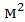)/Вт

Сама стенка 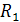= =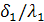0,0002 (К 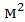)/Вт

Слой накипи 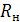= =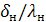0,0019 (К 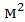)/Вт

Определим температуры на границах слоев и поверхностях стенки после ее эксплуатации

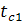=t_ж1-q₃x(1/ 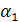)=712,55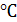

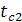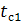= -q₃x( 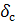/ 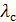)=208,29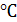

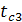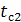= -q₃x( 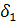/ 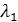)=199,53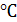

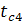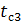= -q₃x( 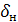/ 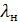)=114,62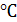

Проверим правильность расчета граничных температур t_ж2= 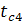-q₃x(1/ 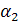)=100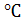

Принимаем удельный тепловой поток через чистую стенку за 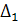=100 % и определим значения удельного теплового потока через стальную стенку после эксплуатации и чистую медную стенку в %

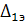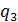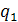=( / )x100%=46%

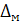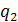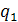=( / )x100%=102%

Задача для самостоятельного решения:

1. По стальному трубопроводу с внешним диаметром dн=120 мм и толщиной стенки δ=6 мм течет газ со средней температурой tг=900°С. Коэффициент теплоотдачи от газа к стенке α₁=52 Вт/(м2•К). Снаружи трубопровод охлаждается водой со средней температурой tв=80°С. Коэффициент теплоотдачи от стенки трубы к воде α₂=4400 Вт/(м2•К). Определить коэффициент теплопередачи от газа к воде, погонный тепловой поток и температуры наружной и внутренней стенки трубы. Тепловой поток считать стационарным. Лучистым теплообменом пренебречь.

Коэффициент теплопроводности стенки трубы l= 45,4 Вт/(м×К).

2.3. Контрольные вопросы

1. Назовите три основные виды теплообмена.

2. Дайте определение теплового потока.

3. Объясните механизм обмена энергии в процессе теплопроводности.

4. Дайте определение конвективного теплообмена.

5. Объясните процесс теплового излучения.

6. Как определить тепловой поток через стенку?

7. Назовите виды процесса конвенции. Объясните их механизм действия.

8. Назовите основные критерии подобия. В чем их физический смысл?

9. Какая схема лежит в основе процесса лучистого теплообмена?

10. Объясните понятие «степень черноты тела».

11. Что такое теплопередача? Приведите пример сложного теплообмена.

12. Как определить сопротивление теплопередачи через многослойную стенку?