Методы решения комбинаторных задач

Задача № 3. Сколько двузначных чисел можно составить с помощью цифр 1, 2, 3 и 4?

Рассуждения ученика.

1 способ. Сначала запишем все числа, у которых в разряде десятков стоит цифра 1: 11, 12, 13, 14.

Затем запишем все числа, у которых в разряде десятков стоит цифра 2: 21, 22, 23, 24.

Запишем числа, у которых в разряде десятков стоит цифра 3: 31, 32, 33, 34.

Запишем числа, у которых в разряде десятков стоит цифра 4: 41, 42, 43, 44.

Получилось 16 чисел: 11, 12, 13, 14, 21, 22, 23, 24, 31, 32, 33, 34, 41, 42, 43, 44. Ответ: 16.

2 способ. Построение дерева возможностей.

Сколько существует способов поставить цифру на первое место? Четыре: цифры 1, 2, 3 или 4. Рисуем от корня 4 веточки и записываем рядом с веточкой цифры 1, 2, 3 и 4.

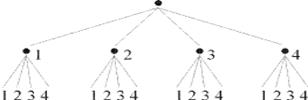
Цифру 1 мы уже поставили на первое место. Сколько у нас есть способов поставить цифру на второе место? Вторую цифру мы можем выбрать четырьмя способами, это может быть цифра 1, 2, 3 или 4. Рисуем от цифры 1 четыре веточки, под каждой подписываем цифру 1, 2, 3 или 4. Считаем внизу число веточек и получаем ответ на вопрос задачи. Таких чисел 16. Есть ли среди записанных чисел число 32? Найдите его. Это десятое число. Все полученные числа: 11, 12, 13, 14, 21, 22, 23, 24, 31, 32, 33, 34, 41, 42, 43, 44.

Задача № 4. «Вороне как – то Бог послал кусочек сыра», брынзы, колбасы, сухарика и шоколада. «На ель Ворона взгромоздясь , позавтракать совсем уж было собралась, да призадумалась»:

Решение:

а) если есть кусочки по очереди, то из скольких вариантов придется выбирать;

б) сколько получится «бутербродов» из двух кусочков;

в) если съесть сразу три кусочка, а остальные спрятать, то из скольких вариантов придется выбирать;

г) сколько получится вариантов, если какой-то кусочек бросить Лисе, а потом ответить на вопрос пункта а)?

Рассуждения учеников:

а) Первый способ. Воспользуемся деревом возможностей:

Таким образом, мы видим, что каждый элемент выбирается 5 способами, остается 4 элемента, из 4-х элементов мы можем выбирать уже 3 способами и так далее.

Получается 2*3=6, 6*4=24, 24*5=120 Ответ:120 способов.

Второй способ. Воспользуемся формулой. Так как элементы можно переставлять и порядок здесь важен, то это перестановка Р_n = n!

И таким образом Р_n = n!=5!=5*4*3*2*1=120 способов. Ответ: 120 способов.

б) Первый способ. Комбинируем элементы.

123, 124, 125, 234, 235, 345, 351, 451, 452, 341. Итого получилось 10 способов перестановки кусочков. Ответ: 10 способов.

Второй способ. Формула.

Так как мы сочетаем элементы, причем элементы не должны повторяться, и порядок не важен, то воспользуемся формулой сочетаний без повторений:

C_n^k = 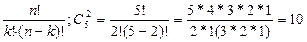Ответ: 10 способов.

в) Первый способ. Также комбинируем кусочки. Те 3 кусочка, которые хотят съесть, мы выбираем из 5 вариантов :

123, 124, 125, 234, 235, 345, 351, 451, 452, 341. Но еще остались спрятанные кусочки, которые мы также выбираем из 5 вариантов. Например, если мы выбрали кусочки 123, то остались 4 и 5, если 124 выбрали, то остались кусочки 5 и 3 и так далее. Образовались еще сочетания, которые представляют спрятанные кусочки: 45, 53, 34, 51, 14, 12, 24, 32, 13, 52. Их тоже 10. Получили следующее: 10+10=20 способов. Ответ: 10 способов.

Второй способ. Применим формулу сочетаний без повторений: C_n^k =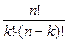

Но само решение будет выглядеть следующим образом:

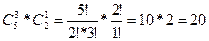Ответ: 20 способов.

г) Брошенный кусочек мы можем выбрать 5 вариантами, а остальные оставшиеся 4 кусочка, которые хотят съесть по очередности, выберем 4!=4*3*2*1, тогда решение будет следующим: 5*4!=5*4*3*2*1=120 способов. Ответ:120 вариантов.

Возможные ошибки:непонимание сути вопроса (задания);незнание формул;слабо развита способность перебирать задание несколькими способами.