Определение среднего коэффициента открытой пористости и объема порового пространства по керну.

Выбор одного из этих методов исследования основывается на характере распределения значений открытой пористости проницаемых образцов, вынесенных из проницаемых интервалов пласта. Дело в том, что при учете данных по керну в связи с его ограниченным выносом единственным способом расчета среднего по залежи (категории запасов) является способ среднеарифметической величины. Вместе с тем, средняя арифметическая величина, являясь состоятельной и несмещенной оценкой, должна быть эффективной, т.е. обладать наименьшей дисперсией по сравнению с другими. Это, в свою очередь, зависит от вида закона распределения случайной величины, в данном случае, открытой пористости.

Многочисленными исследованиями установлено, что статистические распределения значений открытой пористости образцов, вынесенных из проницаемых интервалов продуктивных пластов, не противоречат нормальному закону, для которого средняя арифметическая величина является эффективной оценкой.

Следовательно, чтобы обосновать возможность использования данных керна для расчета среднего значения открытой пористости, студент должен сравнить статистическое распределение значений параметра по исследуемому объекту с теоретической кривой нормального распределения.

В соответствии с изложенным необходимо подготовить исходные данные для проверки согласованности статистического распределения значений открытой пористости проницаемых образцов с кривой нормального распределения. С этой целью следует отбраковать те значения открытой пористости, которым соответствуют некондиционные значения проницаемости и глинистости. Таким образом осуществляется увязка определенных выше кондиционных значений a_сп и т.п. с коллекторскими свойствами пласта по керновым данным.

Для определения кондиционных значений проницаемости и глинистости исследуется статистическая связь между каждым из этих параметров и a_сп. В обработку включаются данные только по тем скважинам, в которых опробованы однородные, по возможности узкие, интервалы, характеризующиеся низкими значениями a_сп и ограниченным разбросом значений проницаемости по интервалу пласта.

Выполнение этих рекомендаций необходимо, чтобы устранить влияние размаха значений проницаемости при переходе со средних на точечные данные. Расчет зависимости ведется с использованием персонального компьютера по указанной выше схеме изучения статистической связи между параметрами.

На основе полученных статистических связей кондиционными принимаются такие значения проницаемости и глинистости, которым соответствует кондиционное значение a_сп, ∆Ig по геофизическим данным.

Установив кондиционные пределы проницаемости, приступают к отбраковке. Первоначально отбраковываются все некондиционные значения проницаемости из проницаемых по геофизическим данным интервалов пласта. Все остальные значения проницаемости исследуются на характер распределения параметра путем сравнения с теоретической кривой логнормального распределения и определения основных характеристик, часть которых будет использована при обосновании коэффициента извлечения нефти.

Для выявления представительных образцов открытой пористости из общего числа определений керна, вынесенного из проницаемых интервалов пласта, учитываются только те значения открытой пористости, которым соответствуют кондиционные значения проницаемости и глинистости, величины которых выше кондиционных.

Подготовленные таким образом данные вводятся в персональный компьютер для расчета оценок основных характеристик распределения открытой пористости и проницаемости, среднего значения 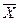, дисперсии S², коэффициента ассиметрии а и эксцесса e, исследования соответствия статистических распределений одной из кривой теоретического распределения. Это соответствие проверяется путем сравнения вычисленных значений критериев согласия 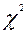Пирсона с критическими, выбираемыми из известной таблицы.

Далее строится график полигонов статистического и теоретического распределений.

Вычисленное значение критерия 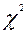Пирсона нужно сравнить с критическим для уровня значимости 0,05 и определенного числа степеней свободы. Последнее равно числу классов минус число независимых условий, наложенных на частоты попадания наблюдений в каждый класс. Таких независимых условий три: число всех наблюдений, число наблюдений в каждом классе и сумма частных от деления второго на первое, равное 1. Если критическое значение больше расчетного, то статистическое распределение не противоречит нормальному закону, и при расчете средней пористости по залежи (зоне) можно пользоваться средним значением, полученным из распределения.

Для определения основных характеристик распределения проницаемости и проверки согласованности его с логнормальным распределением вычисляются логарифмы чисел х_i данной выборки.

В случае если статистическое распределение пористости соответствует нормальному распределению, то имеем дело с однородным коллектором и среднее значение Кп не зависит от его распределения по площади залежи. Что встречается довольно редко.

В том случае, когда статистическое распределение открытой пористости по керну противоречит нормальному закону распределения, для расчета значения этого параметра среднего по залежи используются геофизические данные, предварительно увязанные с керном.