При эксплуатации водозабора в речной долине
Случай плановой фильтрации в безнапорном, однородном и изотропном пласте постоянной мощности без учета инфильтрации можно описать следующим выражением
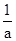
 =
=  , (2.39)
, (2.39)
где а - коэффициент уровнепроводности, который в данном случае может быть выражен в виде:
а = 
Используем метод конечных разностей, заменим соответствующие производные их разностными аналогами.
Первую производную можно заменить


 , (2.40)
, (2.40)
где Δx – шаг по оси X, а вторую производную выражением


 . (2.41)
. (2.41)
Для удобства примем следующую индексацию узлов:
по Х – i = 1,…,7;
по Y – j = 1,…,9,
по Времени – t = 1,…,T,
где Т - время прогноза.
Получим
 = а
= а  (2.42)
(2.42)
Обратим внимание на то, что шаг по X равен шагу по Y, поэтому у второй производной по Y стоит в знаменателе Δx2, вместо Δy2
Перенесем Δt и  вправо, а также вынесем Δ x2 за скобки, получим
вправо, а также вынесем Δ x2 за скобки, получим
 =
= 
 (2.43
(2.43
Следует определить критерий устойчивости явной разностной схемы  , который должен быть меньше или равен
, который должен быть меньше или равен  ,т.е.
,т.е.


 . (2.44)
. (2.44)
В случае его несоответствия следует изменить шаг по времени или по пространственным координатам.
Для однозначного решения дифференциальных уравнений геофильтрации необходимо задание краевых условий - начальные значения искомой функции и значения функции на границах. Так как в наших задачах искомой функцией является функция напора Н, то краевые условия записываются для функции Н или ее производных.
Краевые условия задаются для конкретной области фильтрации - участка земной коры, приуроченного к водоносному горизонту (комплексу) и оконтуренного некоторыми гидродинамическими границами и рассматривается в задаче как единая, гидравлически связанная система. Краевые условия делятся на начальные и граничные.
Начальные условия - исходные значения функции напора в пределах области фильтрации на начальный момент времени. Начальные условия должны быть заданы , для процессов нестационарной геофильтрации, (обычно по результатам измерения напоров в наблюдательных скважинах и их интерполяции) во всех точках области фильтрации в виде
Н(x,y,z,t) It=0 º Н(x,y,z,0). (2.45)
Граничные условия задаются для всех граничных точек области фильтрации (xг, yг, zг) на весь период рассматриваемый при решении данной задачи. Для этого анализируются орогидрографические, гидрогеологические условия, а также учитываются данные опытно-фильтрационных работ и режимных наблюдений. В гидрогеологическом отношении выделяют закрытые границы (угленосная мульда, перекрытая сверху и снизу водоупорными породами). На таких границах фиксируется нулевое значение скорости фильтрации Vn по направлению, перпендикулярному к границе, т.е.
 = 0
= 0
и закрытая граница является линией тока.
При работе инфильтрационного водозабора (речная вода фильтруется через пески) его расходы обычно пренебрежимо малы в сравнении с расходами реки. Поэтому можно предположить, что уровни в реке могут задаваться только исходя из наблюдаемого гидрологического режима реки:
Hг = f (xг, yг, zг, t).
Границу такого рода называют границей обеспеченного питания (контур дна реки).
В плане обычно выделяют полуограниченные и неограниченные области фильтрации, когда, говоря формальным математическим языком одна или все границы удалены в бесконечность.
В математической физике граничные условия подразделяются на граничные условия I , II, III и IY рода.
1. Граничные условия I рода. На границах задано значение напора. Такие условия характерны для:
· рек, водоемов и других границ обеспеченного питания (граница обеспеченного питания когда расход водозабора, расположенного в долине реки пренебрежительно мал по сравнению с расходами реки);
· - естественных контуров стока, приуроченных к нижнему водоупору водоносного пласта;
· - горных выработок, отметка выхода воды в которых также определяется отметкой нижнего водоупора;
· - скважин, работающих с заданным на них напором (самоизливающих, поглощающих).
Частным случаем границ I рода являются границы с постоянным напором, т.е. Н = const.
2. Граничные условия II рода. На границах задано значение расхода Q или нормальной производной  . Такие условия характерны для
. Такие условия характерны для
n закрытых границ ( когда пласт ограничен водоупорными породами);
n границ свободного инфильтрационного питания;
n скважин, работающих с заданным расходом.
3. Граничные условия III рода. На границах задана прямопропорциональная зависимость между расходом и напором, точнее между искомой функцией и ее нормальной производной
 = a H г + b, (2.46)
= a H г + b, (2.46)
где a и b - заданные постоянные. Так как значения H г и  заранее не известны, то условие (2.23) является нелинейным. Условия третьего рода наиболее характерны для контактов водоносного пласта с относительным водоупором, через который идет перетекание или переток воды из открытого водоема, когда роль относительного водоупора играет тонкий слой (мощностью mп) илистых отложений с коэффициентом фильтрации kп. Скорость перетекания, равная, по условию неразрывности, нормальной компоненте скорости фильтрации в водоносном пласте - на границе с относительным водоупоре, - выражается в виде
заранее не известны, то условие (2.23) является нелинейным. Условия третьего рода наиболее характерны для контактов водоносного пласта с относительным водоупором, через который идет перетекание или переток воды из открытого водоема, когда роль относительного водоупора играет тонкий слой (мощностью mп) илистых отложений с коэффициентом фильтрации kп. Скорость перетекания, равная, по условию неразрывности, нормальной компоненте скорости фильтрации в водоносном пласте - на границе с относительным водоупоре, - выражается в виде
Vп = - k  = kР
= kР  , (2.47)
, (2.47)
где
НР - заданный напор в водоеме;
НПЛ - неизвестный напор в пласте, непосредственно под слабопроницаемым слоем.
Согласно условию (2.46) a = kР /mР , b = - kРНР /mР. Заметим, что граница водоема здесь не считается контуром обеспеченного питания и является.
4. Граничные условия IV рода. Границы представляет собой контакт водоносных пород с различными фильтрационными свойствами (граница раздела). Из условий неразрывности потока через эту границу получаем равенство скоростей фильтрации Vn1 иVn2 нормальных ей, или, по закону Дарси
k1  = k2
= k2  . (2.48)
. (2.48)
Кроме того,
Нг1 = Нг2. (2.49)
Дано
Область фильтрации, которая представлена участком речной долины протяженностью 1600 м на 1200 м, разбита сеткой с равномерным шагом по X и по Y и равным 200 м. На безнапорный водоносный горизонт с гидродинамическими параметрами - Кф и m согласно первой работы, m = 0.2. пробурена одна новая эксплуатационная скважина дебитом 150 м3/час.
Постановка задачи
В долине реки проектируется дополнительный водозабор. состоящий из одной совершенной эксплуатационной скважины диаметром 200 мм и с дебитом 150 м3/час. Необходимо вычислить значения функции напора во всех узлах сетки используя выражение (2.5) на двое суток с шагом 1 сутки. По результатам прогноза построить гидроизогипсы. Начальные условия соответствуют результатам лабораторной работы №1 (рис.3). Рассчитать два варианта с граничные условиями I рода, постоянные во времени, т.е. h = const. и с граничными условиями II рода с Q = KF 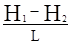 = KFI = const. Шаг сетки -
= KFI = const. Шаг сетки -  x =
x =  y = 200 м. Радиус влияния скважин 200 м. Проектируемые эксплуатационные скважины расположить вне зон взаимовлияния.
y = 200 м. Радиус влияния скважин 200 м. Проектируемые эксплуатационные скважины расположить вне зон взаимовлияния.
Выполнение
Начальные условия (рис.3) следует изменить с учетом ввода в эксплуатацию скважины. Для этого используем выражение
Hc = H0 -  , (2.50)
, (2.50)
где:
Q – дебит скважины;
T – проводимость пласта = kф × m;
Ñ x – шаг сетки;
rc – радиус скважины;
p - 3,14…
n – число сторон блока (сетки).
Скважины располагаются вблизи границ обеспеченного питания (границ водотоков), но не ближе двух узлов сетки от границы водотока, а также не ближе 400 м друг от друга (следует из условия радиуса влияния скважин 200 м). В нашем случае это точка с координатами (5,3). Напор в этой точке с учетом данных задачи составит (2.27)
H5,3 = 100,5 -  =
=
100,5-1,8(0,159*7,6-0,25) = 100,5-1,73 = 98,77 м
Прогноз развития процесса геофильтрации следует начинать с узла h2,2 и используя выражение (2.20) идти по строке hi,2. Затем перейти на строку hi,3 и т.д. Начальными условиями для прогноза на 2-ые сутки будет прогноз на 1-е сутки. Вычисления аналогичны прогнозу на 1-ые сутки. Построение гидроизогипс производится согласно лабораторной работе №1 только на вторые сутки прогноза.
