Тема 4. основные методы расчета систем скважин

Теоретическая часть

Метод сложений течений

Среди аналитических методов используемых для расчета систем скважин эффективно используется метод сложения течений. Рассмотрим общее двумерное уравнение плановой стационарной фильтрации в виде (56) с учетом инфильтрации

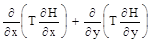+ e = 0. (4.1)

Конкретный выбор этого уравнения не важен, принципиально лишь, чтобы это уравнение было линейным (т.е. T и e не зависят от H).

Пусть H₁ (x,y) и H₂ (x,y) - две функции, удовлетворяющие этому уравнению. Тогда и функция H₃ (x,y) = H₁ (x,y) + H₂ (x,y) также удовлетворяет этому уравнению по принципу суперпозиции. Например: пусть в некотором водоносном горизонте задано естественное распределение напоров H_е (x,y), тогда в соответствии с (4.1) будем иметь

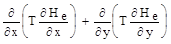+ e (x,y) = 0.(4.2)

В результате водоотбора устанавливается новое распределение напоров - H_в, которое также удовлетворяет уравнению (4.1)

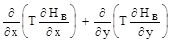+ e (x,y) = 0.(4.3)

Вычитая из уравнения (4.2) уравнение (4.3) получим

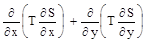= 0.(4.4)

где S = H_е - H_в - понижение напора. В этом примере использование принципа суперпозиции позволило исключить из уравнения инфильтрацию и тем самым упростить математическую постановку задачи.

Развивая идею независимого действия факторов, влияющих на фильтрационный процесс, сформулируем ее для системы водопонижающих скважин: возмущение напора в пласте, обусловленное одновременной работой группы скважин, равно сумме возмущений, вызванных каждой скважиной. Поэтому применительно к задачам геофильтрации принцип суперпозиции может быть назван принципом сложения течений. Рассмотрим его на примере систем скважин.

В неограниченном пласте с исходной горизонтальной пьезометрической поверхностью распределение напоров вблизи одиночной скважины

H( r ) - Н_с= 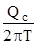ln = ln 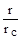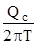r - 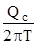ln r_c

или

H( r ) = 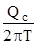ln 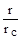= 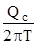ln r - 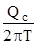ln r_c + Н_с

или

H( r ) = 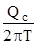ln 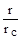= 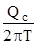ln r + С, (4.5)

где С зависит от условий на скважине.

Так как выражение (4.5) удовлетворяет и общему решению уравнения (4.1), то, согласно принципу суперпозиции, ему удовлетворяет также и сумма

Н = 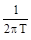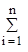Q_ci ln r_i + C_n (4.6)

где n - число скважин; r_i - расстояние от i-ой скважины до точки, в которой ищется напор Н; С_n = 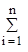C_i - константа, зависящая от условий на скважинах.

Выражение (4.6) является общим решением задачи о работе скважин в неограниченном изолированном напорном пласте.

Учет прямолинейных границ пласта в плане

Влияние прямолинейных границ с условиями первого и второго родов (с постоянным напором и постоянным расходом) эффективно учитывается на основе метода зеркальных отображений, являющимся частным вариантом метода сложений течений.

Полуограниченный пласт

Полуограниченный пласт имеет в плане прямолинейную границу, на которой могут задаваться граничные условия первого, второго или третьего рода.

Прямолинейная граница с условием первого рода (напор Н = const или S = 0)

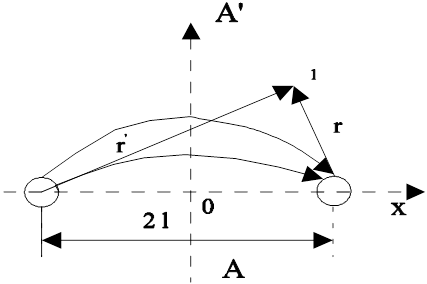
На рисунке изображена скважина, работающая с расходом Q_c в полуограниченном напорном пласте. Границей слева служит контур реки, на котором задано условие первого рода: Н=Н₀ = const.

Для решения этой задачи можно воспользоваться уравнением Тейса

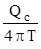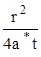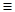
S( r, t ) = - E_i (- ) 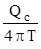W(u), (4.7)

где u 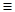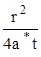и W 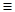- E_i (- u ) предварительно задав фиктивную нагнетательную скважину, представляющую собой зеркальное отображение действующей скважины на расстоянии 2L от действующей.

Для условий откачки с постоянным дебитом Q понижение уровня от действия реальной скважины определится выражением

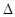Н = 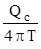W(u); u = 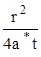. (4.8)

а повышение уровня от действия фиктивной скважины соответственно будет

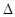Н 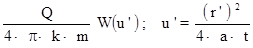^' = . (4.9)

Следовательно, понижение от действия дуплетной системы реальной и фиктивной скважин будет

S = 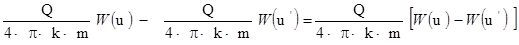; (4.10)

Поскольку на границе r = r ^' и u = u ', то S = 0, так что уравнение (4.10) действительно удовлетворяет граничному условия I рода.

При длительной откачке, когда аргументы u и u' удовлетворяют условию

u = 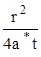= 0.05 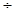0.1

заменяя функции W(u) и W(u') их логарифмическими представлениями, получим

S = 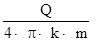. 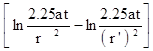= 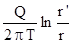, (4.11)

Для определения понижения S_c на стенке скважины в выражениях аргументов u и u' следует положить r = r_c и r' = 2L :

S_с = 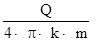. 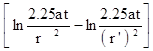= 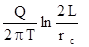(4.12)

впервые доказанную Ф. Форхгеймером.

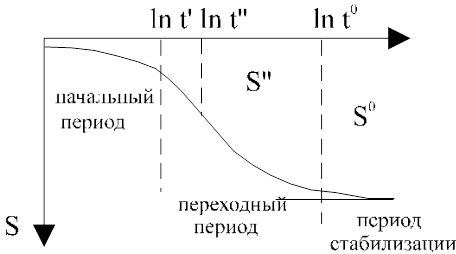
Из уравнения (4.10) обосновывается следующий характер зависимости понижения уровня S от логарифма t: в начальный период еще не сказывается влияние границы, затем наступает переходный период, который завершается асимптотический стабилизацией уровней, стремящихся к значениям S⁰, определяемых по формуле (4.11).

Непроницаемая граница

Такая граница представляет собой наиболее характерный вариант границы второго рода: она учитывается заданием фиктивной откачивающей скважины той же интенсивности, что и действительная, и расположенной симметрично относительно этой границы. Соответственно понижение уровня в этом случае получится сложением понижений создаваемых действительной и фиктивной скважинами, т.е.

S = 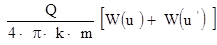, , 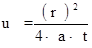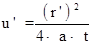. (4.13)

Вследствие симметрии действительной и фиктивной скважин градиент напора (понижения) по оси симметрии будут нулевым, что и соответствует условию, задаваемом на непроницаемой границе.

В начальный период на снижение уровня граница не влияет; затем начинается переходный период, в течение которого влияние границы постепенно увеличивается, и, наконец, наступает период квазистационарного режима, когда можно принять логарифмическое представление функции скважин, т.е.

S = 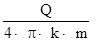. 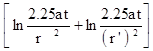= 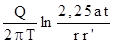. (4.14)

Из выражения (137) следует, что при квазистационарном режиме снижение уровней происходит по той же зависимости, что и в неограниченном пласте, но как бы при удвоенном дебите скважины и расчетном расстоянии, равном .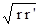

Соответственно график S 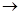ln t в этот период является прямолинейным, но уклон его будет в два раза больше чем в таком же неограниченном пласте (tg a₂ = tg a₁).

Фильтрационное сопротивление геофильтрационного потока

При движении жидкости через горные породы ей приходится затрачивать энергию (напор) на преодоление сил сопротивления. Показателем этих сил может служить потеря напора на некотором участке потока, отнесенная к расходу жидкости через этот участок

Ф = 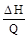. (4.15)

Величина Ф называется фильтрационным сопротивлением потока (на выделенном участке).

Из выведенных формул для одномерного движения нетрудно получить выражения для соответствующих значений фильтрационных сопротивлений. Так, для напорной плоскопараллельной фильтрации

Ф = 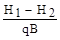= = 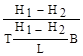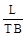(4.16)

где В - фронт потока (ширина), т.е. фильтрационное сопротивление при том же общем расходе потока, естественно, растет с увеличением длины пути фильтрации и с уменьшением проницаемости или фронта потока.

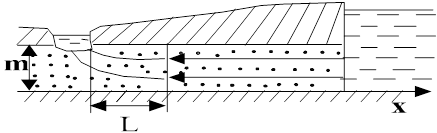
Пусть, например, фильтрация к реке носит преимущественно плановый характер (линии тока горизонтальны), и лишь вблизи реки имеется участок протяженностью L 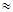m с заметным проявлением вертикальной составляющей скорости, т.е. линии тока искривляются, поперечное сечение потока сокращается и вода испытывает при движении большее сопротивление, чем при плановом движении на участке длиной L. Если мы хотим учесть это обстоятельство, оставаясь в рамках плановой модели, то в ней необходимо изменить фильтрационное сопротивление пласта на участке, прилегающем к реке. Для этого, согласно (139), можно увеличить длину пути фильтрации L на некоторую величину 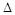L и вести расчет по фиктивной модели пласта, в которой вместо действительного расстояния L берется расчетная величина 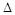L + L.

Количественно величина 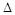L соответствует величине параметра (фактора) перетекания B

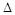L = 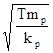(4.17)

Величина L, как видно из (4.17) зависит только от строения ложа водоема, то она может рассматриваться как обобщенный гидрогеологический параметр ложа водоема, характеризующий его фильтрационное сопротивление.

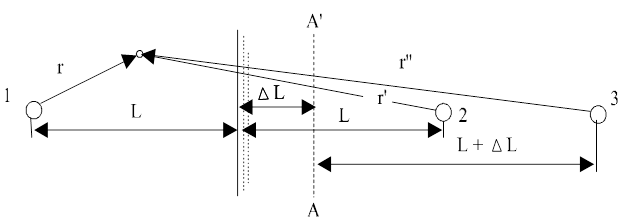
Как правило, характеристики ложа водоема бывают изучены довольно слабо, поэтому наиболее достоверные значения L можно получить только на основе анализа данных режимных наблюдений вблизи водоема. Наиболее удобно и достоверно определение величины L по данным режимных наблюдений за стационарным режимом по створу из двух скважин, заложенных в основной водоносный горизонт вблизи водоема перпендикулярно его урезу при условии, что поток направлен нормально к урезу водоема.

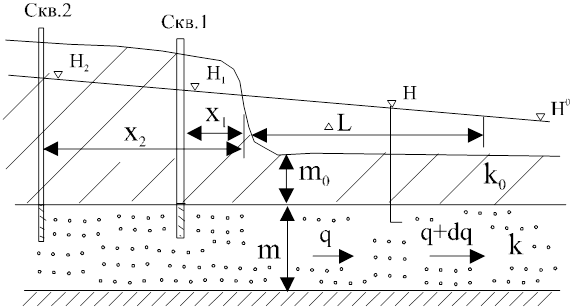
Без учета инфильтрации в пределах створа удельный расход между скважинами 1-2

q = T 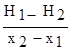. (4.18)

Этот же расход между скважиной 1 и водоемом с учетом перемещения уреза водоема на величину будет

q = T 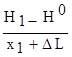. (4.19)

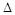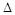Приравнивая (4.18) и (4.19) получим формулу для определения L

L = 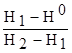( x₂ - x₁) - x₁. (4.20)

В реальных условиях определенные таким образом значения 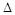L для рек и каналов имеют порядок десятков и сотен метров.

Граница экранированного водоема

Под экранированным водоемом (рис) возникает поток перетекания, который описывается уравнением

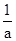
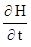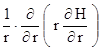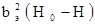= + ,(4.21)

где b₀ = 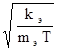- коэффициент перетекания.

Приближенное выражение для нестационарного режима может быть получено введением фиктивного источника, располагаемого от данной точки на расстоянии r'', определяемом по (4.22). В такой постановке нестационарное понижение уровня в плановом потоке определится уравнением

S = 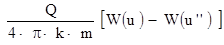, , 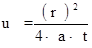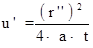. (4.22)

Анализ решение задачи (4.21) показывает, что с высокой точностью здесь можно использовать расчетный прием сдвига уреза водоема на величину 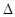L, согласно которому при стационарном режиме фильтрации понижение уровня под влиянием откачки представляется выражением

S = 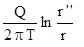, r'' = 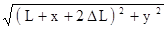, (4.23)

где r'' - расстояние от расчетной точки до отражения скважины относительно сдвинутого уреза водоема. Уравнение (4.23) при 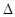L 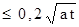дает погрешность результатов менее 2%.

Литература

1. Мироненко, В.А. Динамика подземных вод. [Текст] / В.А. Мироненко - М.:Изд-во МГУ, 1996.-519 с.

2. Миpоненко, В.А. Теоpия и методы интеpпpетации опытно-фильтpационных pабот. [Текст] / В.А.Миpоненко, В.М.Шестаков - М.: Hедpа, 1978. - 325 с.

3. Шестаков, В.М. Динамика подземных вод. [Текст] / В.М. Шестаков -М.:Изд-во МГУ,1979. – 418 с.

Практическая часть