Расчет водопритока с водораздела
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ»
Эколого-гидрогеологическое
Прогнозирование и моделирование
Учебное пособие
Стародубцев В.С.
Издательско-полиграфический центр Воронежского государственного университета
Введение
Учебное пособие по курсу "Эколого-гидрогеологическое прогнозирование и моделирование" предназначено для магистров, обучающихся по профилю экологический менеджмент дневной и заочной форм обучения. Структура пособия состоит из теоретической части, решения практических эколого-гидрогеологических задач и контрольных заданий.
Теория процессов геофильтрации и геомиграции представлена такими разделами как:
Ø основные исходные представления динамики подземных вод;
Ø гидростатический напор фильтрационного потока;
Ø закон Дарси;
Ø емкостные свойства горных пород;
Ø дифференциальные уравнения геофильтрации;
Ø теория скважин;
Ø конвективный перенос в подземных водах;
Ø диффзионно-дисперсионные процессы.
После изучения вводного теоретического курса по изучаемой теме обучающимся предлагается освоить теоретический материал решением соответствующей практической задачи. Решение практических эколого-гидрогеологических задач построено по принципу: "Читай, смотри и делай", т.е. объяснением выполнения отдельных этапов решения задачи с помощью не только формализованного языка, но и большого количества иллюстраций.
Закрепление изучаемых материалов происходит на основе вариантной схемы контрольных заданий по каждой теме курса.
Учебное пособие по курсу "Эколого-гидрогеологическое прогнозирование и моделирование" рекомендуется широкому кругу бакалавров, специалистов, магистров и аспирантов направления подготовки "Геология"
Тема 1. основные исходные представления
Динамики подземных вод
Теоретическая часть
Динамика подземных вод в своих основах исходит из сочетания гидрогеомеханических представлений о процессе фильтрации подземных вод и геологических аспектов условий формирования потоков ПВ.
Следующие представления гидрогеомеханики считаются основополагающими и все основные закономерности выведены с учетом них:
1. Толща водоносных горных пород рассматривается как единая механическая система.
2. Горные породы рассматриваются как сплошное тело, в каждой точке динамические и кинематические характеристики считаются статистически осредненными.
Основное влияние на гидромеханическое состояние водоносной толщи оказывает действие гравитационных сил, в результате воздействия которых происходит гидростатическое обжатие частиц и агрегатов порода и взвешивающие воздействие.
Взвешивающие воздействие, определяемое архимедовыми силами, учитывается выражением
gвз.г = (gм-gв) ( 1-n), (1.1)
где: gвз.г - расчетный вес единицы объема взвешенной горной породы; gм - плотность минерального материала и gв - плотность воды.
Гидростатическое обжатие частиц и агрегатов вызывает сравнительно малые деформации породы, обусловленные незначительной сжимаемостью минеральных частиц. Поэтому напряжения всестороннего обжатия получили название нейтральных, а соответствующее давление (р).
Вертикальное давление (рп), передаваемое на горизонтальную площадку от действия веса вышележащих пород, вызывает в водонасыщенном элементе породы соответствующие напряжения - напряжения в скелете породы (рск) и нейтральное давление воды (р):
рп = рск + р. (1.2)
Изменения в напряженном состоянии пласта, описываемом выражением (1.2), вызывают деформацию воды и скелета породы, приводящую к изменению количества воды и объема порово-трещинного пространства. Учет деформаций воды и скелета породы - упругий режим фильтрации; если же деформации не учитываются - то жесткий режим фильтрации.
Напряженное состояние пласта может изменяться под воздействием гидродинамических факторов (изменение уровней водотоков, взаимодействующих с подземными водами, инфильтрация атмосферных осадков, водоотбор или налив воды в скважины и т.п.) и геодинамических факторов (изменение атмосферного давления на поверхности земли, землетрясений, изменения внешнего давления за счет инженерной деятельности человека (карьеры, выемки, насыпи и т.д.).
Геофильтрация подземных вод.В гидрогеологии под термином фильтрация подземных вод понимается движение свободной гравитационной воды, происходящее под действиемсилы тяжести или градиента давления (при условии полного насыщения свободного пространства водой). Во многих случаях фильтрация ПВ не может быть оторвана от других видов движения воды, существующих в подземной гидросфере планеты. В соответствии с этим в последнее время широко используется (В.М. Шестаков) термин геофильтрация (фильтрация в геологической среде), который объединяет все виды движения воды в горных породах.
Фильтрационный поток.Реальный естественный поток гравитационных подземных вод, фильтрующийся по системе пор или трещин, заменяется условным потоком, который носит название фильтрационного потока ПВ. Его реальная площадь будет определяться выражением
F' = nэф B m, (1.3)
где: B - ширина потока, м; m - мощность потока (пласта), м; nэф - коэффициент эффективной скважности горной породы (отношение объема открытых пустот, по которым происходит (может происходить) движение гравитационной воды, к объему всей породы).
Область фильтрации - это вся область реального потока ПВ или ее часть, в пределах которой намечается количественное изучение движения ПВ. Представленная для выполнения расчетов в упрощенном (схематизированном виде) область фильтрации называется расчетной схемой, если используются аналитические методы, и моделью при применении методов моделирования. Основными характеристиками и элементами области фильтрации являются границы, геофильтрационная среда (определяемая рядом фильтрационных параметром, например коэффициентом фильтрации и т.д.) и краевыми условиями.
Границы подразделяются на естественные и искусственные, внешние и внутренние, проницаемые и непроницаемые.
Под краевыми условиями области фильтрации понимают совокупность граничных и начальных условий. Граничные условия определяют поведение функции напора на границах области фильтрации, а начальные условия - значение функции напора на определенный момент времени.
По условиям залегания и гидравлическому состоянию потоки ПВ разделяют на:
1. Грунтовые;
2. Напорные;
3. Субнапорные;
4. Напорно-безнапорные.
Грунтовые потоки - это воды первого от поверхности Земли выдержанного по площади и постоянно существующего водоносного горизонта, залегающего на первом от поверхности Земли водоупоре, имеют свободную поверхность (давление равняется атмосферному) и капиллярную кайму. Изменение уровня грунтовых вод (ГВ) приводит к изменению мощности водоносного пласта.
Напорные потоки залегают между двумя относительно непроницаемыми слоями, а в разрезе находятся ниже ГВ. Под кровлей напорные воды (НВ) имеют избыточное давление. НВ не имеют капиллярной зоны.
Субнапорные потоки распространены на участках, где свободная поверхность грунтового горизонта располагается в локально распространенных слабопроницаемых породах. При этом под действием избыточного гидростатического давления уровень воды устанавливается выше кровли водоносного горизонта. В этом случае подземные воды называются водами с местным напором или субнапорными.
Напорно-безнапорные потоки - это потоки значительной протяженности, когда на одном участке поток является грунтовым, а на другом напорным.
Расходом фильтрационного потока Qназывается количество воды, проходящее в единицу времени через поперечное сечение потока (см3/с, л/с, м3/сут и т.д.). Поскольку оценка расхода может производиться для потоков (элементов потоков), имеющих различную ширину, введено понятие так называемого удельного (единичного) расходапотока q, под которым понимается количество воды, проходящее в единицу времени через поперечное сечение потока при ширине 1 м (Fед = 1* m, м2, см2).
Скорость фильтрации (скорость фильтрационного потока)- это количество воды, которое проходит в единицу времени через единицу поперечного сечения потока (пласта)
V = 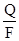 , (1.4)
, (1.4)
где: V - скорость фильтрации (см/с, м/сут и т.д.); Q - расход фильтрационного потока (см3/с, м3/сут); F - площадь поперечного сечения (см2, м2).
Так при расчете скорости фильтрации расход потока отнесен ко всей площади поперечного сечения, поэтому скорость фильтрации не характеризует действительную (истинную) скорость движения воды по "фильтрующему" пространству минерального скелета породы. Действительная скорость движения воды U согласно формуле (1.4) может быть определена из соотношения
U = 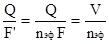 , (1.5)
, (1.5)
где: F' - поперечное сечение свободного "фильтрующего" пространства (см2, м2); nэф - коэффициент эффективной скважинности горной породы, доли единицы.
Из формулы (5) следует, что
V = nэф U, (1.6)
а, поскольку всегда nэф < 1, то U > V.
Рассмотрим теперь понятие гидростатического напора фильтрационного потока (рис.1.1).
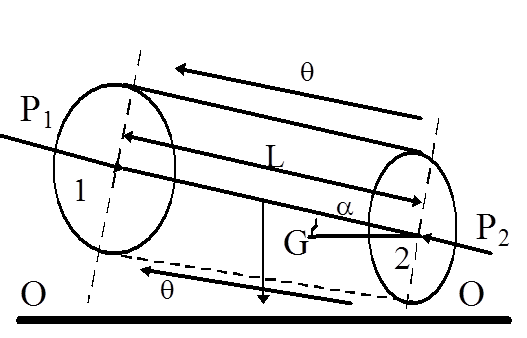
Рис.1.1. Фильтрационная схема по определению понятия гидростатического напора фильтрационного потока
Исходя из постулированных выше представлений фильтрации с позиций механики сплошной среды составим условия равновесия элементарного столбика жидкости длиной L и площадью w (рис.1.1). На торцах этого столбика действуют силы давления
P1= p1w и P2=p2w, (1.7)
где: p1 и p2 - давления в сечениях 1 и 2), направленные вдоль столбика;
в объеме столбика действует его сила тяжести
G = gwL, (1.8)
где g - объемный вес воды; направленная по вертикале; этим силам противодействуют силы сопротивления Q, возникающие по поверхности столбика.
Исходя из равенства проекций действующих сил на направление этого столбика запишем уравнение равновесия
P1 - P2 +G sin a = Q (1.9)
или, имея в виду, что
L sina = z1 - z2, (1.10)
получим0
(p1 - p2) w + g (z1 - z2) w = Q (1.11)
Сгруппируем в левой части этого уравнения величины p и g z для каждого сечения, а в правой части уравнения заменим w на V/ L:
(p1 + g z1) - (p2 + g z2) = 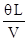 . (1.12)
. (1.12)
Обозначим далее
j = p + g z (1.13)
и приведем уравнение (1.12) к виду
j1 - j2 = 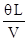 . (1.14)
. (1.14)
Величина (qL ) представляет собой работу, затрачиваемую на преодоление сил сопротивления в элементарном столбике объемом V, а величина 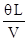 - энергию, затрачиваемую на перемещение единичного объема потока между сечениями 1 и 2, которая по определению должна равняться разнице значений гравита0ционного потенциала в этих сечениях. Из уравнения (1.14) следует, что величина j как раз и представляет собой гравитационный потенциал, поскольку разница его значений определяет собой удельные потери энергии водного потока. Разделив выражение (1.14) на L, получим
- энергию, затрачиваемую на перемещение единичного объема потока между сечениями 1 и 2, которая по определению должна равняться разнице значений гравита0ционного потенциала в этих сечениях. Из уравнения (1.14) следует, что величина j как раз и представляет собой гравитационный потенциал, поскольку разница его значений определяет собой удельные потери энергии водного потока. Разделив выражение (1.14) на L, получим
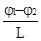 = Ij =
= Ij = 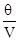 , (1.15)
, (1.15)
т.е. удельные силы сопротивления, действующие в водном потоке, определяются величиной градиента гравитационного потенциала Ij.
В гидравлике водных потоков изменения g обычно не учитываются и тогда вместо потенциала j удобнее использовать гидростатический напор
H = 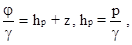 (1.16)
(1.16)
имеющий размерность длины. Гидростатический напор характеризует уровень потенциальной энергии в данной точке потока; в соответствии с выражением (1.13) его величина складывается из высоты давления (пьезометри0ческой высоты) hp = 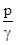 , характеризующей энергию давления в данной точке, и ординаты точки относительно плоскости сравнения z, характеризующей энергию положения в данной точке.
, характеризующей энергию давления в данной точке, и ординаты точки относительно плоскости сравнения z, характеризующей энергию положения в данной точке.
При определении напора ПВ (H) в качестве плоскости сравнения может быть выбрана подошва потока (в случае ее горизонтального положения) или любая горизонтальная поверхность (при условии z1- z2= const). При положении плоскости сравнения на подошве потока напор подземных вод численно равен мощности потока в данном сечении (h1= m1; h2= m2). В реальных условиях при сравнении напора ПВ в различных точках потока в качестве единой плоскости сравнения обычно принимается уровень Мирового океана (z = 0). В этом случае величина напора (м) равна абсолютной отметке уровня до которого поднимается вода под действием гидростатического давления в рассматриваемой точке потока (так называемый установившийся уровень воды). Оценка напора в абсолютных отметках установившегося уровня воды является удобной при необходимости сравнения величин напора ПВ, замеренных в различных точках подземной гидросферы.
Но очевидно, что и в первом, и во втором случаях гидростатический напор отражает запас потенциальной энергии поля силы тяжести в данной точке водоносного пласта. Полная энергия движущегося подземного потока определяется гидродинамическим напором
Hd= hp+ z + 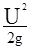 , (1.17)
, (1.17)
где U - скорость движения жидкости.
Величина Hdненамного превышает H. Это можно видеть из такого примера. Если принять скорость движения ПВ 1000 м/сут (для природных условий это весьма большая скорость и встречается довольно редко), то
U = 1000 м/сут 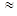
 0,01 м/с, U2/ (2g) = 0.012/ (2∙9.8)=5∙10-6.
0,01 м/с, U2/ (2g) = 0.012/ (2∙9.8)=5∙10-6.
Поэтому слагаемым U2/ (2g) в формуле (1.17) можно пренебречь, а полная энергия подземного потока определяется в основном его потенциальной составляющей, т.е. гидростатическим напором.
При движении жидкости в пористой среде (фильтрация) или движении потока ПВ в естественной среде напор (энергия потока) расходуется на преодоление сил трения (1.15), в связи с чем пьезометрический напор уменьшается (на величину H) по направлению движения потока ПВ. В связи с этим можно считать, что во всех случаях движение ПВ происходит от области (участка, точки и др.) с большим 0напором к области с меньшим напором.
Потеря напора ПВ (H, м) на участке между рассматриваемыми сечениями потока, отнесенная к расстоянию между сечениями (L - длина пути фильтрации, м), называется градиентом пьезометрического напора (напорным градиентом) и определяется из выражения
I = 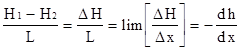 при x = L ® 0. (1.18)
при x = L ® 0. (1.18)
Таким образом, значение напорного градиента (I) характеризует потери пьезометрического напора на единицу длины пути фильтрации. Знак ( - ) в выражении (1.18) указывает, что величина напора уменьшается по направлению движения ПВ (с увеличением Х). Таким образом напряженность поля напоров для подземного потока Eнравна
Ен= - gradH. (1.19)
В гидрогеологии линии напряженности Енназывают линиями тока, а эквипотенциальные поверхности Н - поверхностями равных напоров (изопьез). Линии тока вместе с изопьезами образуют сетку тока или сетку движения. Отметим, что касательные в каждой точке линии тока совпадают с направлением вектора скорости фильтрации. В условиях установившегося движения линии тока совпадают с траекториями движения частиц воды. Линии тока обладают тем свойством, что перпендикулярно к ним расход подземного потока равен нулю, т.е. переноса жидкости через линии тока нет. В изотропных горных породах линии тока перпендикулярны (ортогональны) к линиям равных напоров, поскольку в этом случае направление потока, определяемое направлением вектора скорости, совпадает с направлением максимального градиента, которое идет по нормали к линии равного напора.
Закон Дарси
Основной закон фильтрации был экспериментально установлен французским гидравликом Анри Дарси (1803-1858) на основании опытов по исследованию движению воды через трубки, заполненные песком. По результатам этих опытов А.Дарси сформулировал вывод (закон) о том, что количество воды (Q), проходящей через трубку, заполненную дисперсным материалом, прямо пропорционально разности напоров (Н) в крайних сечениях трубки, прямо пропорционально площади поперечного сечения трубки (F), обратно пропорционально длине трубки (длине пути фильтрации) и прямо пропорционально постоянному для данного материала коэффициенту (К), характеризующему проницаемость материала, заполняющего трубку. Таким образом основной закон фильтрации (закон Дарси) может быть выражен формулой
Q = KF 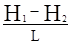 = KFI, (1.20)
= KFI, (1.20)
где F - площадь поперечного сечения трубы, см2; Н1и Н2- значения пьезометрического напора в крайних сечениях, см; L - длина трубки (пути фильтрации), см; К - коэффициент пропорциональности, см/с; I - значение напорного градиента; Q - расход воды (потока), см3/с.
При оценке значения расхода воды через единичное поперечное сечение потока получаем удельный или единичный расход потока q, см3/с, м3/сут:
q = K 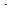 1
1  m
m 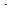
 = K
= K  m
m  I, (1.21)
I, (1.21)
где m - мощность потока, см, м; 1 m = f - площадь поперечного сечения потока при единичной ширине, см2, м2; q - удельный или единичный расход потока см3/с, м3/сут; I - напорный градиент.
При делении обеих частей уравнения (1.20) на площадь поперечного сечения потока (F) получаем
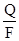 = V = K I, (1.22)
= V = K I, (1.22)
где V - скорость фильтрации, см/с, м/сут.
Эти уравнения (1.20-1.22) являются различными формами выражения основного закона фильтрации, записанного соответственно относительно расхода потока Q, единичного расхода q и скорости фильтрации V.
Коэффициент пропорциональности К, характеризующий проницаемость материала, заполняющего трубку, был назван А.Дарси коэффициентом фильтрации (водопроницаемости). Из выражение (1.22) следует, что коэффициент фильтрации имеет размерность скорости см/с, м/сут и численно равен скорости фильтрации при единичном напорном градиенте.
Коэффициент фильтрации зависит как от свойств самой фильтрующейся жидкости, так и от свойств горной породы. Физически коэффициент фильтрации отражает работу сил трения при движении жидкости в пористой среде (т.е. сил внутреннего трения движущейся жидкости и сил трения жидкости о стенки минерального скелета).
При рассмотрении процессов фильтрации жидкостей с различными свойствами вводится понятие о коэффициенте проницаемости k,который связан с коэффициентом фильтрации следующим соотношением
k = K 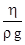 , (1.23)
, (1.23)
где h - коэффициент динамической вязкости, Па/с.
Размерность коэффициента проницаемости k [cм2]. В гидрогеологии более употребительной единицей проницаемости является Дарси (Д), причем
1Д = 1.02 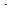 10-6см2= 1.02
10-6см2= 1.02 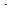 10-12 м2.
10-12 м2.
Один дарси соответствует такой проницаемости, при которой через сечение горной породы с площадью, равной 10-4 м2 объемный расход жидкости равен 10-6м3/с при градиенте давления 10 МПа/м, если вязкость жидкости равна 0.1 Па 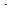 с. Принимая для воды, находящейся в нормальных условиях (температура порядка 20оС), коэффициент динамической вязкости порядка 0.001 Па
с. Принимая для воды, находящейся в нормальных условиях (температура порядка 20оС), коэффициент динамической вязкости порядка 0.001 Па 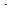 с, получаем, что приближенно проницаемость 1 мкм2 соответствует коэффициенту фильтрации 1 м/сут.
с, получаем, что приближенно проницаемость 1 мкм2 соответствует коэффициенту фильтрации 1 м/сут.
Коэффициент проницаемости в целом не зависит от гидродинамических свойств фильтрующейся жидкости и определяется лишь свойствами горной породы, но вместе с тем следует учитывать возможность горных пород вступать в физико-химическое взаимодействие с водой, на что существенно влияет состав фильтрующейся жидкости. Так, проницаемость песчаников для пресной воды ниже, чем для соленой (для глинистых песчаников это расхождение может достигать двух порядков).
Член уравнения (1.21), являющийся произведением мощности потока (единичной ширины поперечного сечения f = 1 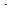 m) на его водопроницаемость (К), называется проводимостью (водопроводимостью) потока или пласта, которая численно равна удельному расходу потока при единичном напорном градиенте (I = 1):
m) на его водопроницаемость (К), называется проводимостью (водопроводимостью) потока или пласта, которая численно равна удельному расходу потока при единичном напорном градиенте (I = 1):
Т = K 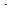 m = q / I, (1.24)
m = q / I, (1.24)
где Т - проводимость пласта, м2/сут.
Границы применимости закона Дарси
При движении капельно-жидкой воды различают два режима течения: ламинарный и турбулентный.
Ламинарный (параллельно-струйный) режим наблюдается при малых скоростях течения; для него характерно движение потока отдельными, не перемешивающимися между собой струйками.
Турбулентный (вихревой) режим наблюдается при сравнительно больших скоростях течения; для него характерно активное проявление внутренней пульсации частиц потока, обусловливающее активное перемешивание между отдельными струйками (образование вихрей).
Помимо ламинарного и турбулентного течений существует переходная область, где проявляются черты и ламинарного, и турбулентного режимов течения.
Для количественной характеристики режима движения жидкости обычно используют безразмерную величину, называемую числом Рейнольдса (Re, Nr)
При движении жидкости в пористой среде число Рейнольдса определяется (Р.Де Уист) из выражения
NR = 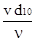 , (1.25)
, (1.25)
где v - скорость фильтрации; n - коэффициент кинематической вязкости жидкости (в СИ - в м2 на секунду).; d10 - эффективный диаметр (под действующеим, или эффективным , диаметром частиц d10 или def понимается размер частиц, соответствующий ординате 10% на суммарной кривой механического состава).
Тем самым значение числа Рейнольдса зависит от скорости фильтрации и диаметра частиц минерального скелета породы, определяющего размеры пустот и, следовательно проницаемость горной породы.
Критической скорости течения, определяющей границу ламинарного режима, соответствует критическое число Рейнольдса Reкр. По данным Р.Де Уиста значение Nr, при котором происходят отклонения от линейного закона фильтрации, изменяется в зависимости от размера частиц и пористости горной породы в пределах от 2 до 5. По Н.Н. Павловскому критическое число Рейнольдса находится в пределах от 7 до 9.
В обобщенной форме основной закон фильтрации выражается (А.Дарси, Ф.Форхгеймер) двучленной зависимостью вида
I = av + bv2 = 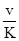 (1 + av), (1.26)
(1 + av), (1.26)
где а = 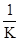 , b =
, b = 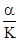 - фильтрационные параметры; K - коэффициент фильтрации при ламинарном режиме; a - коэффициент нелинейности фильтрации, который приближенно может быть вычислен как
- фильтрационные параметры; K - коэффициент фильтрации при ламинарном режиме; a - коэффициент нелинейности фильтрации, который приближенно может быть вычислен как
a = aо 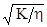 , (1.27)
, (1.27)
где aо - параметр, зависящий от пористости и структуры порового пространства; для сравнительно однородных несцементированных пород
aо = 0.09 / (n2 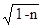 ) . (1.28)
) . (1.28)
Наряду с существованием верхней границы применимости закона Дарси ( при относительно больших скоростях фильтрации) оказывается, что проявляется также и нижняя граница справедливости этого закона (при малых скоростях фильтрации). При очень малых скоростях фильтрации в тонкодисперсных породах нарушение закона Дарси (нижний предел применимости) связано с проявлением сил молекулярного взаимодействия частиц воды и породы при вязкопластичном характере течения воды в субкапиллярных пустотах (табл.1.1).
Таблица 1.1
Виды скважинности (пустотности) горных пород в зависимости от размеров
(Справочное руководство, 1979 г.)
| Вид скважности | Диаметр пор d, мм | Ширина трещин l, мм |
| Субкапиллярная | < 0.0002 | < 0.0001 |
| Капиллярная | 0.0002 - 0.5 | 0.0001 - 0.25 |
| Сверхкапиллярная | > 0.5 | > 0.25 |
По существующим представлениям (И.К.Гавич, 1988) физически связанная вода, заполняющая субкапиллярные пустоты, остается неподвижной до определенных, достаточно больших, значений напорного градиента (Io - начальный градиент фильтрации). При I > Io происходит сложное движение с постепенно увеличивающимся значением проницаемости горной породы (K), поскольку увеличение градиента определяет переход в подвижное состояние дополнительных количеств связанной воды. При 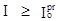 (предельное значение начального градиента) все возможное количество связанной воды вовлекается в движение, и основной закон фильтрации может быть записан в виде
(предельное значение начального градиента) все возможное количество связанной воды вовлекается в движение, и основной закон фильтрации может быть записан в виде
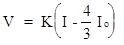 . (1.29)
. (1.29)
По другим представлениям (И.А. Бриллинг, В.М. Гольдберг, Н.П.Скворцов), фильтрация в тонкодисперсных породах происходит при всех значениях напорного градиента, однако в области очень малых значений напорного градиента это движение не фиксируется при современной технике лабораторных экспериментов. Величина начального напорного градиента определяет в этом случае только область нарушения линейного закона фильтрации.
Литература
1. Мироненко, В.А. Динамика подземных вод. [Текст] / В.А. Мироненко - М.:Изд-во МГУ, 1996.-519 с.
2. Миpоненко, В.А. Теоpия и методы интеpпpетации опытно-фильтpационных pабот. [Текст] / В.А.Миpоненко, В.М.Шестаков - М.: Hедpа, 1978. - 325 с.
3. Шестаков, В.М. Динамика подземных вод. [Текст] / В.М. Шестаков -М.:Изд-во МГУ,1979. – 418 с.
Практическая часть
Расчет водопритока с водораздела
Лабораторная работа предназначена для уяснения лекционных тем "Гидростатический напор подземных вод", "Закон Дарси" Рассмотрение области фильтрации подземных вод как объекта исследований при изучении гидродинамических закономерностей геофильтрации всегда бывает затруднено малым количеством фактических данных. Это, прежде всего, относится к гидродинамическим параметрам пласта. Важнейшим среди них является напор подземных вод, который входит как искомая функция во все дифференциальные уравнения геофильтрации. Преодоление этих затруднений связано с применением методов интерполяции функций.
Интерполяция (от латинского interpolatio – обновление, переделывание, изменение) – приближенное или точное нахождение какой-либо величины по известным отдельным значениям этой же или других величин, связанных с ней. В первоначальном понимании – восстановление функций (точное или приближенной) по известным её значениям в заданных точках. В гидрогеологии применяется для построения различных карт и подготовки начальных условий при решении дифференциальных уравнений геофильтрации численными методами. Наиболее популярны кусочно-линейная интерполяция, кусочно-квадратичная интерполяция, интерполяция квадратичными сплайнами. В лабораторной работе используется кусочно-линейная интерполяция.
Пусть надо вычислить f(x) для х 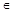 [хi , хi+1], h = хi+1 - хi. Тогда суть кусочно-линейной интерполяции состоит в том, чтоиспользуется линейное приближение
[хi , хi+1], h = хi+1 - хi. Тогда суть кусочно-линейной интерполяции состоит в том, чтоиспользуется линейное приближение
f(x) 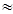 fi +
fi + 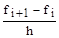 (x - xi). (1)
(x - xi). (1)
Для случая равномерной сетки на отрезке [i,j] выражение (1) преобразуется к виду
fi+1 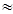 fi +
fi + 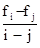 , (2)
, (2)
где i и j – номер узла сетки.
Таким образом, непрерывная функция напора заменяется в области фильтрации дискретной (сеточной) функцией, значения которой известны лишь в некоторых узлах сетки и с помощью методов интерполяции находятся ее значения во всех узлах сетки.
Дано
Область фильтрации, которая представлена участком речной долины протяженностью 1200 м на 1600 м, разбита сеткой с равномерным шагом по X и по Y и равным 200 м, где значения функции напора известны лишь в отдельных узлах сетки (рис.1).
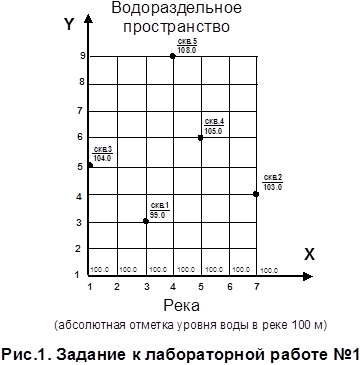 |
Постановка задачи
Необходимо найти значения функции во всех узлах сетки, построить линии равных напоров с шагом 0.5 метра и линии тока.
Используя линии гидроизогипс и закон Дарси
Q = Kф F 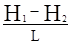 = Kф F I,
= Kф F I,
где F - площадь поперечного водоносного пласта, м2; Н1и Н2- значения напора в рассматриваемых сечениях, м; L - длина пути фильтрации, м;
Кф - коэффициент фильтрации, м/сут; I = 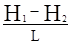 - значение напорного градиента; Q - расход потока, м3/сут,
- значение напорного градиента; Q - расход потока, м3/сут,
рассчитать водоприток в речную долину, учитывая, что Кф = 40 м/сут, а m (мощность водоносного пласта) = 50 м.
Выполнение
Для удобства примем следующую индексацию узлов:
по Х - i = 1,…7;
по Y – j = 1,…9.
Тогда получим обозначение значения напора в узле Hi,j. Например значение напора в скважине №4 можно записать как H5,6 = 105.0 м.
Принимаем, что на водораздельном пространстве напор во всех узлах одинаков (H1,9 = H2,9 = … =H4,9 =…= H7,9). Находим значения напора в оставшихся граничных узлах (левая и правая границы). Для этого интерполируем значение напора между узлами H1,1 и H1,5, H1,5 и H1,9, а также между H7,1 и H7,4, H7,4 и H7,9 согласно выражению (2). Например:
H1,2 = H1,1 + 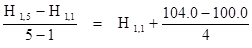 = H1,1 +1 = 100 + 1 = 101.0 м
= H1,1 +1 = 100 + 1 = 101.0 м
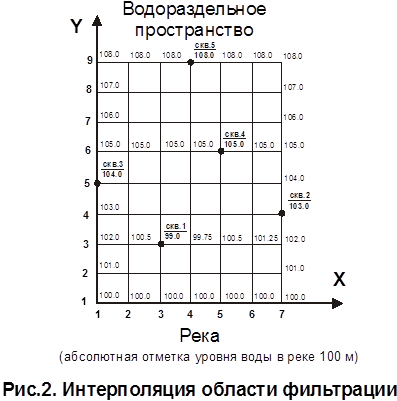 |
Используя известные внутренние точки H3,3 и H3,7 находим значения напора в узлах Н 1,3 – H 3,3 и Н 3,3 – H 7,3 и аналогично Н 1,6 – H 5,6 и Н 5,6 – H 7,6 (рис.2).
Интерполяция заканчивается нахождением значений напора в промежуточных строках (H i,2, H i,4, H i,5, H i,7, H i,8). Для этого последовательно интерполируем между строками H i,3 - H i,1, H i,6 - H i,3, H i,9 - H i,6 (рис.3).
В гидрогеологии линии напряженности называют линиями тока, а эквипотенциальные поверхности Н - поверхностями равных напоров (для напорных потоков – гидроизопьезы, для безнапорных - гидроизогипсы).
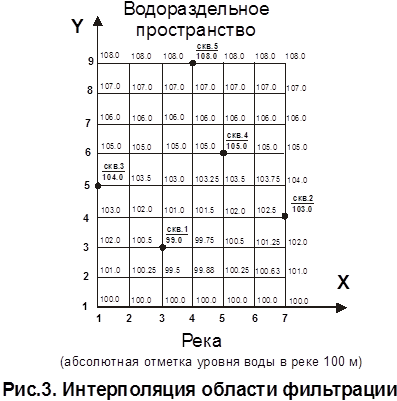 |
Линии тока вместе с гидроизогипсами образуют сетку тока подземных вод. В изотропных горных породах линии тока перпендикулярны к линиям равных напоров, поскольку в этом случае направление потока, определяемое направлением вектора скорости, совпадает с направлением максимального
градиента, которое идет по нормали к линии равного напора.
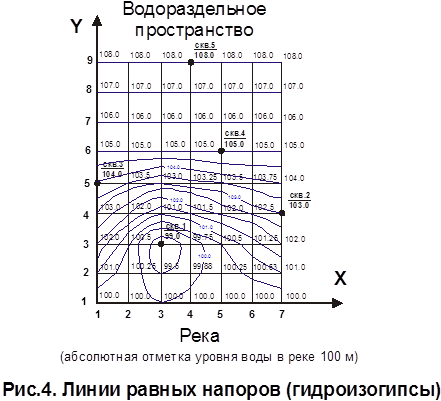
Построение линий равных напоров (гидроизогипс) аналогично процессу интерполяции узлов сетки области фильтрации. Отличие состоит лишь в том что интерполяция идет теперь по отдельным узлам. Так, между узлами Н 2,3 – H 3,3 следует найти точки прохождения гидроизогипс 99,5 м и 100,0 м. Заметим, что интерполяция должна проводится как по горизонтальной, так и по вертикальной осям. Гидроизогипсы 105,0-108,0 совпадут с линиями сетки, так как радиус влияния ЭС №1 составляет » 400 м (рис.4).
 |
Линии тока целесообразно строить в местах изгиба линий равных напоров (рис.5).
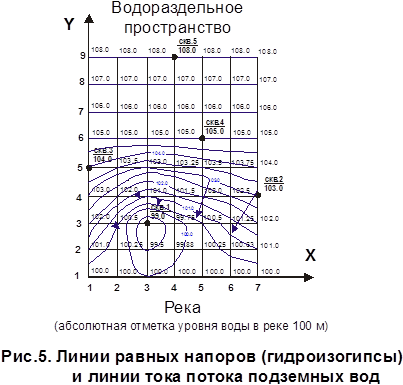 |
Для определения водопритока выбираем параллельные линии гидроизогипс (чтобы снизить погрешность при определении площади поперечного сечения потока подземных вод) и с учетом шага сетки вычисляем водоприток в речную долину со стороны водораздела. Например:
Q = Kф F 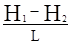 = Kф F
= Kф F 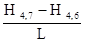 =
=
= 40м/сут (50 м x 200 м х 6) 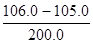 = 12000 м3/сут.
= 12000 м3/сут.
Варианты заданий
