Предварительная обработка данных
Итак, выяснено, что для классификации пространственных объектов необходимо иметь географическую карту этих объектов и матрицу объект-признак, строки которой соответствуют ОТЕ. Но проводить классификацию еще рано, к ней нужно подготовиться, иначе результаты (если они вообще будут получены) невозможно будет интерпретировать. Нулевым этапом классификации ОТЕ является их предварительная обработка, часто включающая нормировку, взвешивание, снижение размерности, агрегирование и идентификацию.
В ходе предварительной обработки важно определить тип каждого признака. Обычно выделяют количественные и качественные признаки. Качественные признаки подразделяют на порядковые (ранговые) и номинальные. Для порядковых признаков можно говорить лишь о том, что одно значение больше (меньше) другого, но неизвестно, на сколько (например, «Уровень образования»). И наконец, для номинальных признаков можно вести речь только о совпадении или несовпадении значений (например, «Название субъекта РФ», «Статус субъекта РФ»). Количественные признаки характеризуют, на сколько или во сколько раз одно значение больше (меньше) другого. Например, признаки «Действительных бюллетеней», «Количество голосов, отданных за кандидата X», «Явка избирателей в процентах».
Нормировка. Нормировка используется для приведения анализируемых признаков к единым масштабу и точке отсчета. Наиболее часто применяют следующие виды нормировки.
- Нормировка по заданному показателю:
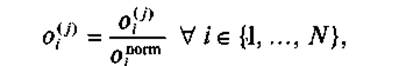
где о(j) – исходный признак; j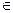 
{1,..., М); onorm – нормирующий признак.
Данную нормировку часто используют в социально-экономической географии. В качестве нормирующих признаков при этом могут выступать общая численность населения ОТЕ или площадь занимаемой ОТЕ территории. Примеры использования нормировки по заданному показателю: плотность населения (нормировка численности населения ОТЕ площадью, занимаемой ОТЕ); процент голосов, отданный на выборах за какую-либо политическую партию (нормировка числа проголосовавших за партию в данной ОТЕ общим числом избирателей); валовой внутренний продукт (ВВП) страны на душу населения (нормировка ВВП общим числом граждан).
Пример. Перевод признака «Против всех» к признаку «Против всех, %» от признака «Действительных бюллетеней» (табл. 2).
Таблица 2
| Название субъекта РФ | «Действительных бюллетений» (onorm) (у"огт) | «Против всех» (о(j)) | «Против всех, %» |
| Москва | 4 606 632 | 67 351 | 1,46= (67351/ 4606632)*100 |
| Омская область | 1 076 469 | 22 553 | 2,10= (22553/ 1076469)*100 |
| Калужская область | 1,54=(9194/598476)*100 | ||
| Бурятия | 5 820 | 1,45= (5820/ 400288)*100 |
Нормированные подобным образом признаки могут принимать различные действительные значения.
- Нормировка по дисперсиям и математическим ожиданиям:
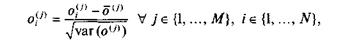
где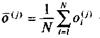 
– оценка математического ожидания j-го показателя; 
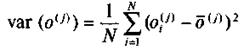– оценка дисперсии j-го показателя.
Данную нормировку используют в случае, если анализируемые признаки имеют различную природу и несоизмеримы. После проведения нормировки в предположении о нормальности распределения признака он с большой вероятностью принимает значения в диапазоне (-3; 3).
Пример. Нормировка признака «Против всех, %» (Москва), табл.3:
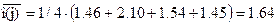
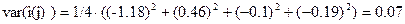
Таблица 3
| Название субъекта РФ | «Против всех, %» о(j) | «Против всех, нормированный»  |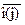
| Москва | 1,46 | -0,69( -0,18/0,26) |
| Омская область | 2,10 | 1,77(0,46/0,26) |
| Калужская область | 1,54 | -0,38(-0.1/0,26) |
| Бурятия | 1,45 | -0.73(-0.19/0.26) |
- Нормировка по наилучшим или наихудшим значениям:
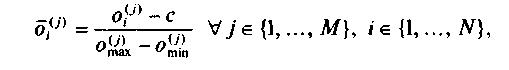
где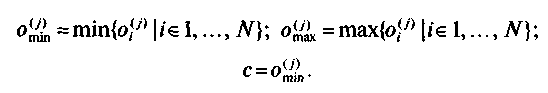 
Полученные в результате нормировки по наилучшим или наихудшим значениям числа ограничены отрезком [0,1]. Иногда в формулу нормировки вводят умножение на 100, изменяя диапазон значений на отрезок [0,100].
Таким образом, нормированные значения лежат в привычном человеку интервале и могут интерпретироваться как наилучшие или наихудшие в процентном соотношении.
Пример. Нормировка признака «Против всех, %» (Бурятия), табл. 4. Пусть с =оmin(j) = 1,45;
оmax(j) - оmin(j) = 2,10 - 1,45 = 0,65.
Таблица 4
| Название субъекта РФ | «Против всех, %» ои) | «Против всех, нормированный» |
| Москва | 1,46 |  |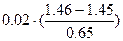
| Омская область | 2,10 |  |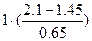
| Калужская область | 1,54 |  |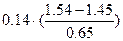
| Бурятия | 1,45 |  |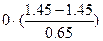
При проведении анализа данных на компьютере нет нужды запоминать формулы нормировки. Необходимо только выбрать из перечня доступных способов нормировки способ, наилучшим образом соответствующий характеру решаемой задачи. В системе GisCluster 2.0 способ нормировки задается выбором элемента ниспадающего списка.
Взвешивание. Процесс назначения весов для показателей (взвешивание показателей) необходим для корректного проведения географических классификаций. Зачастую, по аналогии с различными единицами измерения показателей, различны и их вклады, значимость для данной предметной области. Веса обычно задаются экспертным способом и являются числами, по модулю не превосходящими единицы (например, 0,9, -0,5). Если для системы признаков вектором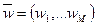 
заданы веса, то пересчет значений признаков осуществляется по формуле:
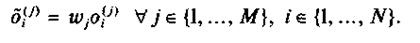
При расчете на компьютере от эксперта требуется ввод весов в каком-либо формате, понятном автоматизированной системе. Например, это может быть название отдельного признака, значения которого интерпретируются как веса.
Снижение размерности. Анализ главных компонент – один из методов снижения размерности атрибутивного признакового пространства. Данный метод используется, в частности, для уменьшения влияния взаимных корреляций признаков и снижения трудоемкости последующих процедур классификации. С практической точки зрения необходимо знать, что параметрами метода главных компонент являются либо процент дисперсии, который необходимо сохранить в новой системе признаков (например, 75 %, 90%), либо число наиболее информативных признаков, которые желательно получить (например, 3). Управляя этими параметрами в конкретной автоматизированной системе (например, статистическом пакете Statgraphics 5.x или специализированной ГИС GisCluster 2.0), можно значительно улучшать результаты классификации.
Агрегирование. Агрегирование в наиболее простой интерпретации является одним из методов перехода от множества исходных показателей к единственному, по которому следует различать ОТЕ. Чаще всего результирующий показатель получают таким образом, чтобы ОТЕ с его минимальными значениями могли интерпретироваться как «плохие», а с максимальными - как «хорошие» (в разрезе проблемы, описываемой показателями), или наоборот.
В географических исследованиях используют обычно следующие методы, позволяющие получить единственный результирующий признак o(agr)= (o1(agr),..., oN(agr)):
1) суммирование значений предварительно нормированных и взвешенных показателей: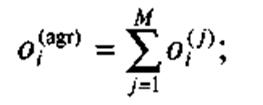 
2) расчет расстояний в многомерном признаковом пространстве до наилучшей или наихудшей (возможно условной) ОТЕ о':
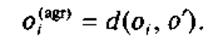
Способы расчета расстояний в многомерном признаковом пространстве рассмотрены ниже.
Идентификация. До начала классификации многомерных данных в ГИС необходимо установить связь между внешней таблицей и слоем карты, чтобы однозначно сопоставить ОТЕ-точке многомерного признакового пространства ОТЕ-географический объект. Физически это означает установление связи между атрибутивной и внешней таблицей, что является стандартной операцией баз данных. Связь между двумя таблицами устанавливается по одинаковым уникальным полям (столбцам), которые обычно имеют числовой тип. Если каждая таблица содержит по такому числовому полю, то проблемы идентификации не существует, однако чаще всего обе таблицы содержат только текстовые поля названий ОТЕ. Соединение таблиц можно осуществить и по этим полям, но практика показывает, что написание одних и тех же географических названий сильно отличается. Эти различия наиболее остро проявляются в сокращениях типа «обл», «обл.» или «область», «г.», «гор.» или «город» и т.д. Кроме того, иногда встречаются и синонимические названия для одной и той же ОТЕ.
Чаще всего проблема идентификации решается вручную. В некоторых специализированных пакетах (например, ГИС GisCluster 2.0) предложены полуавтоматические процедуры идентификации.
Методы классификации
По степени учета географического пространства методы классификации подразделяют на использующие и не использующие географическое пространство. Типичным примером использования при классификации географического пространства является районирование, т. е. получение компактных сгущений ОТЕ одновременно в двух признаковых пространствах – географическом и атрибутивном.
По наличию обучающей выборки бывают методы классификации «с учителем» и «без учителя».
По наличию априорной информации о статистических свойствах классов методы классификации подразделяют на параметрические и непараметрические. Целью параметрических методов (например, ЕМ-алгоритма) является отыскание неизвестных параметров известных функций распределения ОТЕ в пределах каждого класса и вероятностей появления этих классов. Непараметрические методы обычно делят на иерархические (агломеративные и дивизимные) и неиерархические (чаще всего ядерные).
Практически важным является знание специфики конкретного метода классификации, условий его применения, а также задаваемых параметров. Рассмотрим с позиций данного тезиса некоторые иерархические и ядерные алгоритмы.
Расчет расстояния между ОТЕ. Общим параметром для иерархических и ядерных алгоритмов является способ задания метрики, т. е. формула расчета расстояния между двумя ОТЕ в пространстве признаков. Необходимость измерять расстояние между ОТЕ диктуется постановкой задачи классификации.
Для расчета расстояния на М количественных признаках существует наиболее общее соотношение, называемое метрикой махалонобисского типа. Частными случаями расстояния махалонобисского типа являются:
• евклидово расстояние
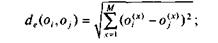
• манхэттенское расстояние
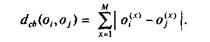
В качестве меры близости ОТЕ в пространстве числовых признаков иногда используется коэффициент корреляции, вычисленный для ОТЕ.
При проведении практического анализа необходимо придерживаться следующих рекомендаций:
• применение евклидова расстояния теоретически обосновано в случае нормального распределения признаков, независимости признаков и равенства дисперсий признаков;
• манхэттенское расстояние логично применять в случае дискретности значений признаков;
• использование расстояния типа корреляции позволяет нивелировать разницу между абсолютными значениями признаков, акцентируя внимание на степени соответствия значений двух ОТЕ по всему комплексу признаков. Используется при большом числе признаков.
Пример. Рассмотрим следующую матрицу ОТЕ-признак (табл. 5).
| Название субъекта РФ | Количество | голосов, % |
| за Б.Н.Ельцина | «Против всех» | |
| Москва | 61,73 | 1,46 |
| Бурятия | 31,26 | 1,45 |
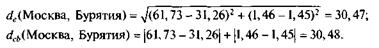
Ядерные методы классификации. Суть ядерных методов классификации достаточно проста. Предполагается, что существуют «ядра» – некоторые реальные или гипотетические ОТЕ, являющиеся типичными представителями своего класса по всему комплексу признаков. Первоначальные ядра могут находиться с помощью обучающей выборки, выбираться случайным образом или с использованием эвристических алгоритмов. На каждой итерации алгоритма к выделенным ядрам последовательно присоединяются ближайшие с точки зрения выбранной метрики ОТЕ. Критерием останова ядерного алгоритма классификации по минимальности расстояний является просмотр и отнесение к ядрам всех ОТЕ, не являющихся ядрами. Ядерный алгоритм «k-средних» после проведения классификации пересчитывает ядра путем нахождения в каждом сформированном классе новой наиболее типичной ОТЕ и продолжает классификацию до тех пор, пока ядра не перестают изменяться.
Дополнительным параметром ядерных алгоритмов является количество классов, которое требуется сформировать.
Ядерные методы классификации следует применять в тех случаях, когда имеется обучающая выборка (т.е. информация о ядрах классов). Трудоемкость ядерных алгоритмов достаточно низкая, поэтому данные методы следует использовать при ручной обработке информации либо при автоматической обработке информации большого объема.
Иерархические дивизимные методы классификации. Суть данных методов классификации состоит в разбиении на очередной итерации одного из полученных на предыдущей итерации классов на несколько классов (обычно два). На первой итерации все ОТЕ относят к одному классу. Критерием останова дивизимных методов является либо достижение заданного количества классов, либо соответствие каждой ОТЕ отдельному классу.
Иерархические агломеративные методы классификации. В отличие от дивизимных агломеративные методы классификации на каждой итерации последовательно объединяют два или несколько существующих классов в более крупный. Критерием объединения классов является их близость. После получения нового класса пересчитываются все расстояния от него до других классов. Отличием агломеративных процедур классификации является формула расчета межклассовых расстояний, которая основана на расчете расстояний между отдельными ОТЕ. Выбор межклассового расстояния настолько влияет на результат классификации, что зачастую вносится в название алгоритма (например, «агломеративный алгоритм средней связи»).
Чаще всего используют следующие виды межклассовых расстояний:
• Метод ближнего соседа. Расстояние между двумя классами рассчитывается как расстояние между двумя ближайшими ОТЕ этих классов:
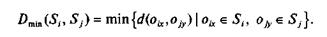
Недостатком метода является то, что при наличии в выборке аномальных наблюдений (т.е. таких, которые существенно отличаются по своим значениям показателей от остальных OTEI они будут помещены в отдельные классы. Основная группа ОТЖ «сольется» в один большой класс. Таким образом, метод следует использовать при отсутствии аномальных наблюдений либо для их отыскания;
• Метод дальнего соседа. Расстояние между двумя классами рассчитывается как расстояние между двумя самыми дальними ОТЕ этих классов:
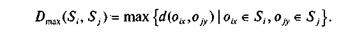
Данный метод более устойчив к образованию одного представительного класса и тяготеет к формированию соизмеримых пс количеству ОТЕ классов;
• Центроидный метод. Расстояние между двумя классами рассчитывается как расстояние между центрами классов:
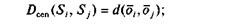
Иерархические методы классификации (особенно агломератив-ные процедуры) являются более трудоемкими по сравнению с ядерными алгоритмами.
• Метод группового среднего (средней связи):
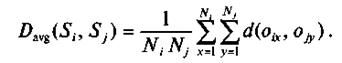
Преимуществом таких методов является возможность их применения без наличия априорной информации о свойствах классов (например, ядер классов или обучающих выборок). Модификация для географического районирования, применение при неизвестном числе классов и наглядная визуализация хода и результатов классификации показана на графике, называемом дендрограммой (рис. 1).
Рис.1.
На оси абсцисс графика изображаются ОТЕ (в том порядке, в котором они объединялись или разъединялись), по оси ординат – либо шаг алгоритма, либо расстояние между вновь объединяемыми (разделяемыми) классами. Два объединяемых (разъединяемых) класса соединяются П-образной линией, нижние концы которой упираются в середины двух классов, а длины вертикальных отрезков равны расстоянию между классами.
ЗАДАЧИ
В задачах 1–9 использовать следующую матрицу ОТЕ-признак. Условия задач приведены в табл. 6.
| Регион | Смертность | Ожидаемая продолжительность жизни, лет | |||
| Младенческая | Мужчины | Женщины | Мужчины | Женщины | |
| Карелия | 13,2 | 2 294,0 | 1 208,2 | 58,1 | 71,3 |
| Коми | 16,9 | 2548,1 | 1 203,6 | 58,2 | 70,4 |
| Архангельская обл. | 15,9 | 2 270,9 | 1 109,1 | 58,5 | 72,1 |
| Ненецкий автономный округ | 23,8 | 2 270,9 | 1 109,1 | 58,5 | 72,1 |
| Вологодская обл. | 17,4 | 2 278,8 | 1045,7 | 58,9 | 72,8 |
| Мурманская обл. | 17,3 | 1 973,5 | 1 107,0 | 60,1 | 71,5 |
| г. Санкт-Петербург | 11,5 | 1 807,0 | 945,9 | 62,6 | 73,8 |
| Ленинградская обл. | 11,3 | 2 330,7 | 1 144,8 | 58,8 | 71,7 |
Задача 1. Определите тип каждого признака.
Задача 2. Проведите нормировку признаков:
а) по дисперсиям и математическим ожиданиям;
б) по наилучшим значениям;
в) по наихудшим значениям.
Задача 3. Взвесьте значения признаков (см. рекомендации по весам в подразделе «взвешивание»).
Задача 4. Проведите агрегирование признаков:
а) методом «взвешенной суммы»;
б) расчетом расстояния до наилучшей ОТЕ (евклидова метрика);
в) расчетом расстояния до наихудшей ОТЕ (манхэттенская метрика).
Задача 5. Постройте матрицу попарных близостей с использованием следующих видов расстояний:
а) евклидово;
б) манхэттенское;
в) корреляции.
Задача 6. Примените ядерный алгоритм классификации в случае:
а) случайного выбора ядер, евклидовой метрики и К= 3;
б) выбора в качестве ядер наиболее отличающихся друг от друга ОТЕ, манхэттенской метрики и К= 2.
Задача 7. Примените алгоритм средних три раза, каждый раз случайно выбирая другую пару первоначальных ядер (евклидова метрика, К= 2). Объясните полученные результаты.
Задача 8. Примените дивизимный алгоритм членения графа близостей в случае:
а) евклидовой метрики;
б) манхэттенской метрики.
Объясните полученные результаты.
Задача 9. Примените агломеративный алгоритм для евклидовой метрики и следующих типов расчета межклассовых расстояний:
а) метод ближнего соседа;
б) метод дальнего соседа;
в) центроидный метод;
г) метод группового среднего.
Постройте дендрограммы. Оцените по дендрограммам возможное число классов. Объясните различие в получаемых результатах.
Контрольные вопросы
1. В чем состоит цель классификации пространственных объектов?
2. В чем различие между следующими понятиями «классификация», «сегментация», «кластеризация», «таксономия», «типология», «группировка», «оценка»?
3. Поясните специфику классификации в геоинформатике.
4. Перечислите типы операционно-территориальных единиц в ГИС.
5. Для каких целей осуществляется предварительная обработка данных?
6. Что относится к количественным признакам и что они характеризуют?
7. Качественные признаки объектов.
8. Для каких целей осуществляется нормировка признаков?
9. Перечислите виды нормировки.
10. В чем состоит процесс назначения весов признаков?
11. Основные задачи процессов «снижение размерности», «агрегирование», «идентификация» признаков объектов.
12. Для каких целей осуществляется расчет расстояния между ОТЕ?
Задание на практическую работу:
1. Ответить на контрольные вопросы к теоретической части работы.
2. Решить задачи 1-5.