Определение координат точек P, Q, Z
| Параметр | M - P | P - Q | Q - Z | Z - N |
| d | 12,00 | 28,00 | 13,00 | 20,32 |
| x1 Dx x2 | +1197,07 +6,47 +1203,54 | +1203,54 +15,10 +1218,64 | +1218,64 +7,01 +1225,65 | +1225,65 +10,96 +1236,61 |
| y1 Dy y2 | +2402,06 +10,10 +2412,16 | +2412,16 +23,58 +2435,74 | +2435,74 +10,95 +2446,69 | +2446,69 +17,11 +2463,80 |
Таблица 30
Определение длин линий
| Параметр | M – A, м | P – A, м | Q – B, м | Z – B, м |
| x1 x2 Dx | +1197,07 +1206,60 +9,53 | +1203,54 +1206,60 +3,06 | +1218,64 +1230,67 +12,03 | +1225,65 +1230,67 +5,02 |
| y1 y2 Dy | +2402,06 +2405,20 +3,14 | +2412,16 +2405,20 - 6,96 | +2435,74 +2437,14 +1,40 | +2446,69 +2437,14 - 9,55 |
| d | 10,03 | 7,60 | 12,11 | 10,79 |
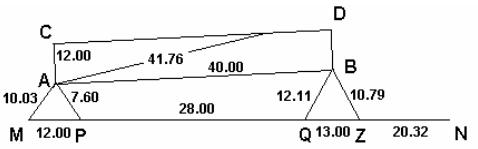
Рис.33. Разбивочный чертеж при разбивке способом линейных засечек
Для контроля измеряют оси здания AB и CD, а также диагонали AD и CD.
Определение неприступного расстояния.
Определять неприступное расстояние можно по:
1)теореме синусов.В практике геодезических измерений бывают случаи, когда измерить непосредственно линию на местности нельзя, например, через реку, овраг и т.д. (рис.34). В таком случае задачу можно решать по теореме синусов. Для определения расстояния АВ = d лентой измеряют расстояние АС = b1, называемое базисом, теодолитом – горизонтальные углы b1 и b2 между базисом и направлением на точку В. Длину базиса выбирают так, чтобы угол при точке В был близок к 90°.Искомое расстояние найдется из треугольника АВС по формуле:
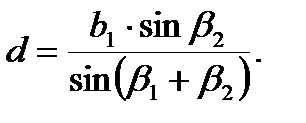
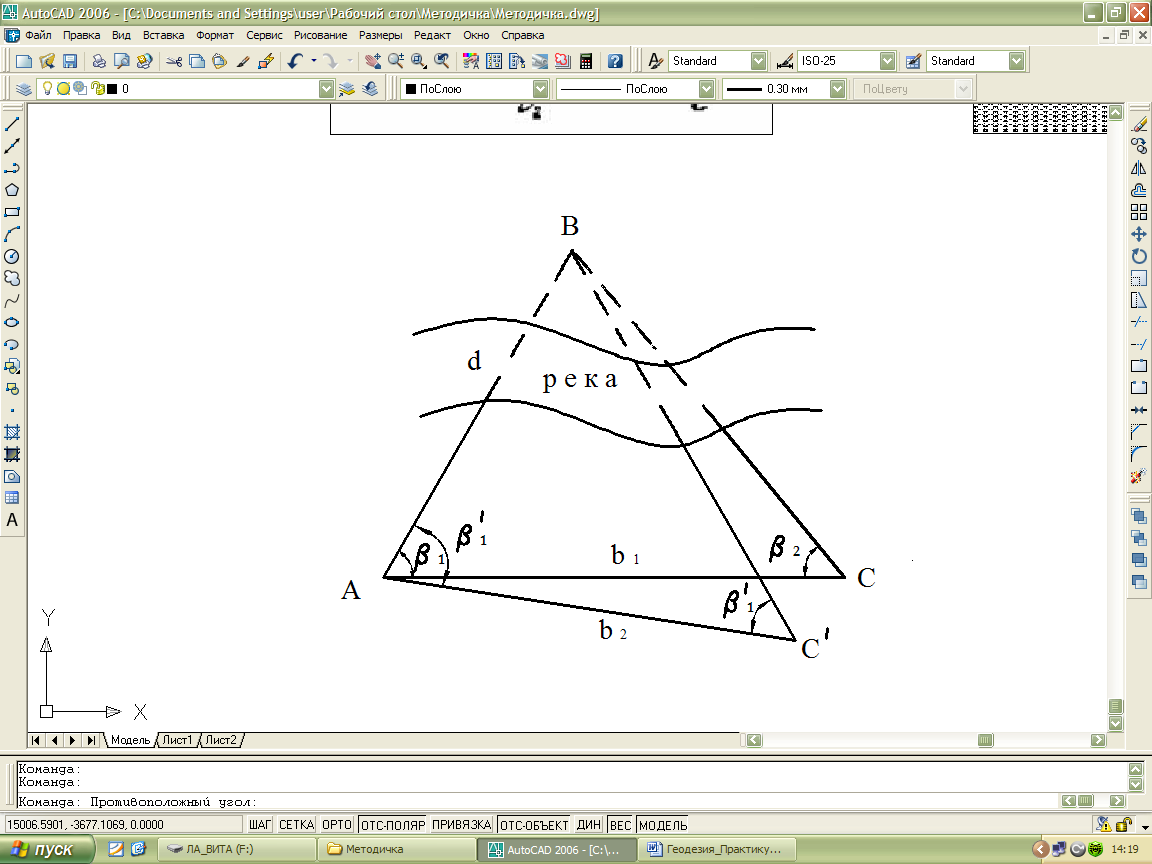
Рис.34. Схема определения неприступного расстояния по теореме синусов
Для контроля определения расстояния d произвольно смещают на небольшое расстояние точку С в положение С' и в полученном треугольнике АВС' производят аналогичные измерения, т.е. измеряют базис b2и горизонтальные углы b1' и b2'. Расстояние d'
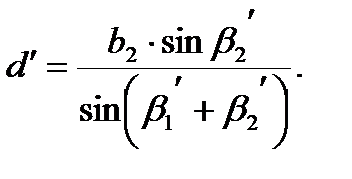
Расхождение между расстояниями, полученными из двух треугольников, не должно превышать 1:1500 определяемого расстояния, т.е.
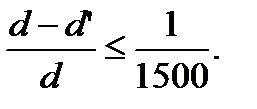
За окончательное принимается среднее из двух определений;
2)теореме косинусов.Если между точками А и В нет взаимной видимости, то для определения расстояния АВ может быть использовано другое построение (рис.35). Разбивают два базиса с общей точкой С так, чтобы из этой точки была видимость на точки А и В. Оба базиса а и bизмеряют стальной лентой, а теодолитом измеряют горизонтальный угол b. Тогда искомое расстояние можно определить по теореме косинусов:
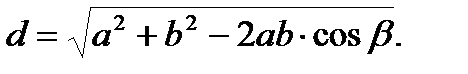
Для контроля аналогичным образом выбирается точка С1,вновь производятся измерения базисов a1, b1и угла b1 и вычисляется искомое расстояние.
При расхождении полученных значений d и d' не более 1:1500 находится средняя величина расстояния АВ.
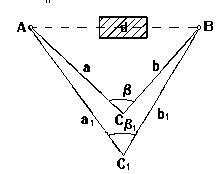
Рис.35. Схема определения неприступного расстояния по теореме косинусов
Определение высоты сооружения.
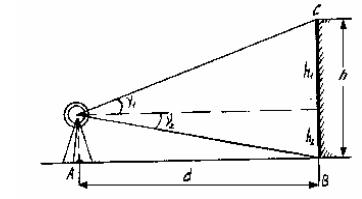
Для определения высоты сооружения, например, здания (рис. 36), в точке А, расположенной на расстоянии примерно 1,5 высоты сооружения, устанавливают теодолит и измеряют углы наклона n1 и n2, визируя на верхнюю и нижнюю точки здания. Измеряют расстояние АВ = d и определяют высоту здания по формуле
h = d× (tgn1 - tgn2) .
При использовании формулы необходимо учитывать знак угла наклона.
Если линия местности АВ наклонна и равна D, то нужно измерить ее наклон nD и вычислить горизонтальное проложение d.
За окончательное значение h берут среднее, если расхождение не более 1: 300 высоты измеряемого сооружения.
Рис. 36. Схема определения высоты сооружения
Пример определения высоты сооружения приведен в табл.31. Углы наклона измерялись теодолитом 2Т30.
Относительная ошибка определения высоты сооружения получилась равной
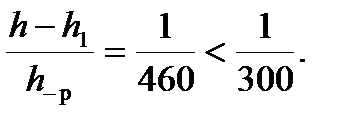
Таблица 31
