Методом наименьших квадратов

Зависимость измеряемой величины y от условий опыта х может быть найдена графически, если нанести значения х и у на миллиметровую бумагу и построить плавную кривую так, чтобы точки равномерно распределились по обе стороны кривой

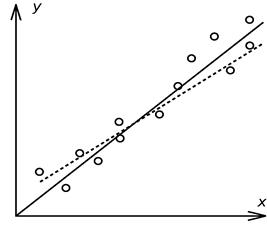
(рис. 1). Задача состоит в том, чтобы по результатам опытов построить такую кривую у = f(x), относительно которой разброс (отклонения) экспериментальных точек был бы минимальным.

В теория вероятности показано, что наилучшее приближение к истинной зависимости у = f(x) дает прямая линия, построенная методом наименьших квадратов. В этом случае сумма квадратов отклонений экспериментальных значений у_i от кривой у = f(x) будет минимальна. Отсюда и происходит название данного метода обработки результатов эксперимента.

Рис. 1. Метод наименьших квадратов

1. Рассмотрим применение метода наименьших квадратов для случая, когда между измеряемыми величинами хиу существует линейная зависимость

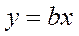. (1)

Пусть в результате эксперимента получено п различных значений величины у_i, соответствующих различным значениям величины х_i . Найдем коэффициент b,при котором экспериментальные точки у_i будут иметь наименьшие отклонения Δу_i относительно прямой.

Отклонение каждого значения у_i от прямой у = bх будет

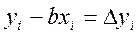. (2)

Составим сумму квадратов отклонений:

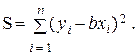(3)

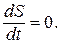Отклонение (разброс) измеренных значений у_i от функции у = f(x) будет минимальным, если

(4)

Дифференцирование (3) по переменной b (предположив, что все остальные величины постоянны) с учетом (4) дает

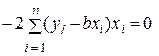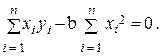или (5)

Отсюда определяем искомый коэффициент b.

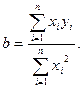(6)

2. В случае линейной зависимости между величинами х и у, которая аппроксимируется прямой, не проходящей через начало координат,

y = a + bx, (7)

коэффициенты а и b могут быть вычислены по формулам

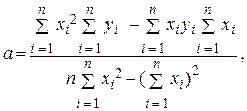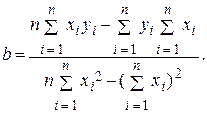(8)

Пример: предположим, что мы провели эксперимент и получили данные, которые занесли в табл. 1.

Таблица 1

Номер измерения i
xi	1,0	1,9	3,1	4,0	4,9
yi	1,6	2,5	3,0	3,7	4,6

Для упрощения расчетов составим вспомогательную таблицу и заполним ее.

Таблица 2

Номер измерения i	xi	yi	xi уi	xi2
	1,0	1,6	1,60	1,00
	1,9	2,5	4,75	3,61
	3,1	3,0	9,30	9,61
	4,0	3,7	14,80	16,00
	4,9	4,6	22,54	24,01
Σ	14,9	15,4	52,99	54,23

Рассчитаем коэффициенты а и b

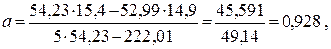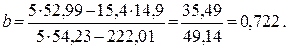Таким образом, уравнение прямой будет выглядеть следующим образом: у = 0,928 + 0,722· х .

Для построения отрезка прямой линии найдем две точки, одна

у₁= 0,928. Вторую точку y₂ получим, подставив в уравнение прямой значение х, равное, например, 5.

у₂ = 0,928 + 0,722·5 = 4,538 .

На листе миллиметровой бумаги проведем оси координат, причем ось у проведем вертикально, а ось х – горизонтально.

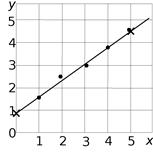
Рис. 2.

Выберем и нанесем на оси координат масштаб так, чтобы наши экспериментальные точки располагались на графике наилучшим образом – занимали на графике максимальную площадь. Нанесем на график экспериментальные точки и две точки у₁и у₂, рассчитанные нами (рис. 2). Для обозначения экспериментальных и «теоретических» точек используем разные обозначения (кружки, крестики, треугольники и т. п.).

Через две «теоретических» точки (y₁и y₂) проведем отрезок прямой линии. При правильных расчетах линия пройдет на графике наилучшим образом, так, что экспериментальные точки будут располагаться справа и слева от прямой линии. Все построения следует делать карандашом.

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

1. Братухин Ю.К. Обработка результатов измерений: учеб. пособие / Ю.К.Братухин, Г.Ф. Путин. – Пермь.: Изд-во Перм. гос. ун-та, 1989. – 44 с.

2. Колесниченко В.И. Обработка и представление результатов эксперимента: учеб. пособие / В.И. Колесниченко.- Пермь: Перм. гос. техн. ун-т, 2000. – 74 с.

3. Зайдель А.Н. Ошибки измерений физических величин А.Н. Зайдель. – Л.: Наука, 1985. – 108 с.

4. А.Н. Паршаков Принципы и практика решения задач по общей физике. Часть 2. Электромагнетизм: учеб. пособие /

А.Н. Паршаков, - Пермь: Изд-во Перм. гос. техн. ун-та, 2010. – 313 с.

СОДЕРЖАНИЕ

Основные правила работы в лабораториях кафедры

прикладной физики ………………………………………….. 3

Лабораторная работа № 1. Изучение электронного

осциллографа ………………………………………………….5

Лабораторная работа № 2. Исследование

электростатического поля с помощью электропроводной

бумаги………………………. …………………………………14

Лабораторная работа № 3. Измерение емкости конденсатора

и диэлектрической проницаемости…………………………...19

Лабораторная работа № 4. Изучение зависимости мощности

и к.п.д. источника тока от нагрузки………………………… 23

Лабораторная работа № 5. Измерение горизонтальной

составляющей магнитного поля Земли………………………27

Приложения ……………………………………………………32

Список рекомендуемой литературы ………………………….36