Обратная геодезическая задача

По заданным координатам точки 1(х₁; у₁) и координатам точки 2 (х₂; у₂) найти дирекционный угол линии, соединяющей точки 1 и 2 (a), расстояние между точками (d).

На рис. 11,а видно, что из прямоугольного треугольника 1А2

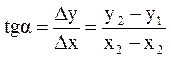, отсюда .

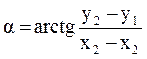Расстояние между точками 1 и 2 определится по формулам:

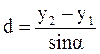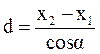, и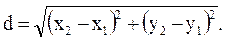

На практике используются следующие математические выражения:

,

, .

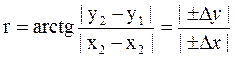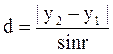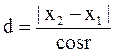В зависимости от номера четверти, в которой находится румб, дирекционный угол α₁ = r₁, α₂ = 180º – r₂, α₃ = 180º + r₃ и α₄ = 360º – r₄;

Пример. Дано: х₁ = 220,00 м, у₁ = 250,00 м, х₂ = 120,00м, у₂ = 150,00 м. Найти: a и d.

Найдем числовое значение румба r.

.

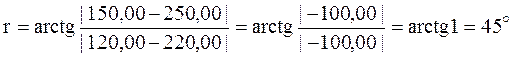Приращение по оси Y отрицательное (Δу = – 100,00), приращение по оси X также отрицательное (Δх = – 100,00), следовательно, румб находится в третьей четверти, а в этой четверти

α = 180º + r = 180° + 45° = 225°.

Расстояние между точками

,

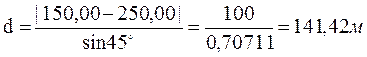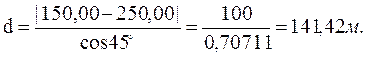
ГЕОДЕЗИЧЕСКИЕ СЕТИ

Общие сведения о геодезических сетях

При составлении карт и планов и решении геодезических задач на поверхности земли устанавливают пункты (точки), для которых известны координаты Х (абсцисса), У (ордината) и Н (высота). Совокупность таких пунктов, координаты которых получены в единой системе, называют геодезической сетью. Геодезические сети подразделяют на плановые (пункты характеризуются координатами Х и У) и высотные (для пунктов получены высоты Н). Геодезические сети развиваются методами триангуляции, трилатерации, полигонометрии и нивелирования.

Триангуляция – это построение на местности примыкающих друг к другу треугольников, в которых измерены все углы и одна сторона какого-либо треугольника, называемая базисом. Схема триангуляции показана на рис. 14.

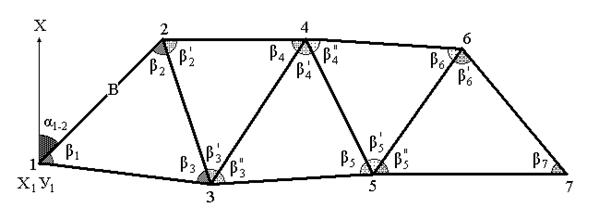
Рис. 14. Триангуляция

Цель триангуляции – получение плановых координат вершин треугольников. Координаты находят путем применения прямой геодезической задачи.

Например, для получения координат точки 2 имеются все необходимые данные: координаты исходной точки 1 (Х₁ и У₁) длина стороны 1-2 (L_1-2 = В) и дирекционный угол α_1-2. Координаты точки 2:

Х₂ = Х₁ + L_1-2 ·cоsα_1-2,

У₂ = У₁ + L_1-2 ·sinα_1-2.

Координаты точки 3:

Х₃ = Х₂ + L_2-3 ·cоsα_2-3,

У₃ = У₂ + L_2-3 ·sinα_2-3.

Здесь неизвестными являются длина L_2-3 и дирекционный угол α_2-3. Длина стороны 2-3 находится путем решения треугольника 1 2 3 по теореме синусов, т. е.

.

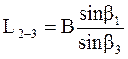Дирекционный угол α_2-3 = α_1-2 + 180 – β₂.

Трилатерация – это построение на местности примыкающих друг к другу треугольников, в которых измерены все стороны треугольников. На рис. 15 это стороны L_1-2, L_2-3, L_3-1, L_2-4, L_3-4, L_3-5, L_4-5, L_4-6, L_5-6, L_5-7, L_6-7.

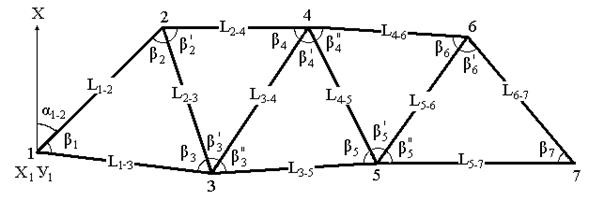
Рис. 15. Трилатерация

Цель трилатерации – получение плановых координат вершин треугольников, которые также как и в триангуляции вычисляются по формулам прямой геодезической задачи.

Для получения координат точки 2 имеются все необходимые данные: Х₁ и У₁, α_1-2 и L_1-2.

Координаты точки 2:

Х₂ = Х₁ + L_1-2 ·cоsα_1-2,

У₂ = У₁ + L_1-2 ·sinα_1-2.

Координаты точки 3:

Х₃ = Х₂ + L_2-3 ·cоsα_2-3,

У₃ = У₂ + L_2-3 ·sinα_2-3.

Неизвестным является дирекционный угол линии 2-3 α_2-3, который вычисляется по формуле

α_2-3 = α_1-2 + 180 – β₂.

В этой формуле неизвестен угол β₂, который может быть получен по теореме косинусов:

.

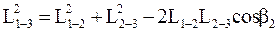Полигонометрия – построение на местности замкнутых или разомкнутых ломаных линий и измерение длин линий и углов между этими линиями. На рис. 16 приводится разомкнутый полигонометрический ход, в котором измерены правые по ходу углы β₁, β₂, β₃, β₄, и длины линий L_1-2, L_2-3, L_3-4, L_4-5.

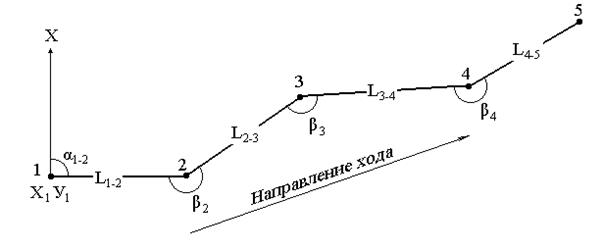
Рис. 16. Полигонометрия

Цель полигонометрии – получение плановых координат точек хода 2, 3, 4, 5. Здесь также используются формулы прямой геодезической задачи.

Координаты точки 2:

Х₂ = Х₁ + L_1-2 ·cоsα_1-2,

У₂ = У₁ + L_1-2 ·sinα_1-2.

Координаты точки 3:

Х₃ = Х₂ + L_2-3 ·cоsα_2-3,

У₃ = У₂ + L_2-3 ·sinα_2-3.

В этих формулах неизвестен дирекционный угол α_2-3, который вычисляется по формуле

α_2-3= α_1-2 + 180 – β₂.

Нивелирование – это процесс определения превышений между точками и вычисление высот точек (рис. 17). При заданной высоте первой точки H₁ и полученных путем измерений превышений h₁, h₂, h₃, h₄ и h₅ высоты остальных точек поверхности земли вычисляются по следующим формулам:

H₂ = H₁+ h₁, H₃ = H₂+ h₂, H₄ = H₃+ h₃, H₅ = H₄+ h₄ и т. д.

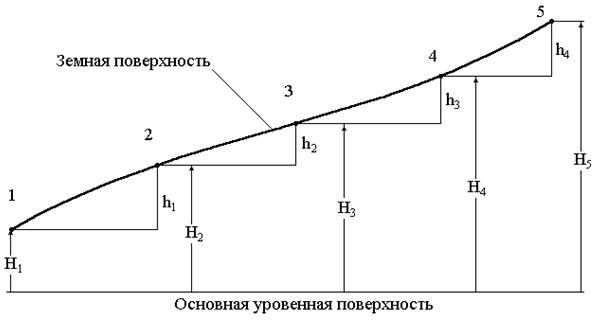
Рис. 17. Нивелирование

Геодезические сети (плановые и высотные) делятся на 4 вида:

1) государственные;

2) сгущения;

3) съемочные;

4) специальные.

Государственные геодезические сети подразделяются на 4 класса (I, II, III и IV). Эти сети служат основой для построения других видов сетей и различных топографических съемок.

Государственные геодезические сети развиваются по принципу "от общего к частному", т. е. от крупных и точных построений к мелким и менее точным. В качестве примера можно привести некоторые данные по триангуляции (плановая сеть) I, II, III и IV классов (табл. 1).

Допустимая невязка в сетях нивелирования (высотная сеть) II, III и IV классов составляет 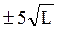, , 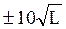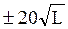мм соответственно.

Геодезические сети сгущения создаются, когда в отдельных районах недостаточное количество пунктов государственной геодезической сети. Они развиваются методами триангуляции, полигонометрии, нивелирования и делятся на сети 1-го и 2-го разрядов.

Таблица 1