Методы оценки качества эталонных сигнатур классов в пакете ERDAS Imagine. Средства отображения сигнатур классов в пространстве признаков

В редакторе сигнатур можно выполнить предварительную оценку качества контролируемой классификации по сформированным сигнатурам классов. Для таких целей используются функциональные характеристики взаимного положения классов, связанные с ожидаемой ошибкой классификации. Чем больше значение используемого критерия разделимости, тем меньше должны быть ошибки при разделении оцениваемых классов, В пакете ERDAS Imagine предлагается четыре вида оценок: евклидово расстояние, дивергенция (прямая и трансформированная) и расстояние Джеффриса-Матуситы.

Евклидово расстояние между средними значениями по классам удобно использовать в тех случаях, когда классы достаточно однородны по яркости, то есть образуют небольшие компактные области в пространстве признаков. Чем больше расстояние между средними по классам, тем меньше вероятность ошибки. Такая оценка, как и метод классификации по минимуму расстояния, в этом случае оказывается эффективной.

В таких мерах разделимости, как дивергенция и расстояние Джсффриса-Матуситы, учитываются отношения между вероятностями появления признака в каждом из классов, поэтому их обыкновенно используют при классификации статистическими методами (по расстоянию Махаланобиса или максимуму правдоподобия). Чем выше значения этих величин, тем меньше будет ожидаемая величина ошибки. Дивергенцию (трансформированную дивергенцию) удобнее использовать в тех случаях, когда сигнатуры классов распределены в признаковом пространстве более или менее равномерно, расстояние Джеффриса-Матуситы пригодно практически для любых ситуаций, однако оценивает соотношения между вероятностями по классам более грубо.

Данные оценки особенно полезны в тех случаях, когда обучение выполняется по выделенным на изображении тестовым участкам. Именно потому, что такие сигнатуры часто имеют большую диаграмму рассеяния и могут сильно перекрываться в пространстве признаков,

Чтобы выполнить оценку разделимости для Ваших сигнатур, выделите оцениваемую группу классов и выберите в редакторе сигнатур функцию Evaluate > Separability. Установите радиокнопку на выбранный Вами критерий оценки. Вы получите протокол, в котором будут указаны средние и минимальные значения по группе и отдельно по парам классов. Для выбранного критерия выполняется как усредненная оценка разделимости, так и минимальная (наихудшая).

Для оценки ошибок первого и второго рода по тестовым участкам изображения при использовании конкретного классификатора (решающего правила) используется фунция Evaluate > Contingency. На выходе выдается протокол, в котором показывается сколько точек из класса К[ попало в класс к₂ для всей совокупности классов.

На основании этих оценок Вы можете как оценить качество обучающих данных, так и подобрать наиболее подходящий метод классификации.

Меры статистической разделимости обучающих выборок для статистической классификации, их характеристика и обоснование использования. Меры статистической разделимости в пакете ERDAS Imagine. Проверка качества обучения на тестовых участках.

Обучение классификаторов - задача достаточно сложная, и ее особенности существенно зависят от сферы приложения алгоритма. В общем случае необходимо проведение целого ряда исследований: прежде всего, выбор гипотезы о типе статистического распределения используемых признаков в каждом из классов и затем проверка этой гипотезы на репрезентативных выборках по объектам исследования. В тематической обработке многозональных аэрокосмических изображений это один из самых проблематичных этапов. Помимо ограничений конкретного алгоритма классификации, результат, который мы получаем на выходе, зависит еще и от следующих факторов.

1.От способа синтеза изображения при выводе на экран и особенностей палитры. В процессе синтеза так или иначе происходит некоторая потеря информации, обусловленная самой математической моделью

процесса. Кроме того, индивидуальные особенности восприятия человеком цветовой гаммы влияют на способность аналитика различать объекты исследования и, следовательно, на процесс формирования обучающих выборок.

2.От достоверности наземных данных, в том числе от способа их сбора и точности координатной привязки тестовых участков к изображению. Даже при разрешении цифрового на местности 30-50м мы едва ли сможем строго привязать точечные измерения. Следовательно, для надежного обучения классификатора необходимы тестовые участки с высокой степенью пространственной однородности. При работе с материалами наземных обследований это еще один довод в пользу двухэтапной схемы обработки: сначала выполнение неконтролируемой классификации с целью выбора однородных участков для получения наземных данных, потом проведение наземных обследований, затем классификация с обучением. В настоящее время, однако, такой схемой пользуются редко из-за высокой стоимости детальных наземных обследований и ищут другие пути решения этой проблемы.

3.Наконец, от количества и способа расположения обучающих выборок на изображении. Изменчивость спектральных отражательных свойств объектов земной поверхности даже в пределах одного изображения может оказаться очень высокой. Кроме факторов, обусловленных условиями съемки и учитывающихся в процессе нормализации изображений, на отражательные характеристики объектов могут повлиять такие факторы, как ветер, осадки и т.п.

Предположим, тем не менее, что мы получили вполне надежные обучающие выборки и рассчитали параметры функций плотности распределения для всех классов. Каким способом можно оценить возможности удовлетворительной классификации конкретных данных при выбранных описаниях классов, то есть ожидаемые вероятности ошибок? Для этой цели используется такое понятие, как статистическая разделимость.

Статистическая разделимость классов- это некоторая функциональная характеристика, известным образом связанная с вероятностью ошибки классификации.

Как мы уже видели при рассмотрении статистического классификатора, вероятность ошибки при разделении пары классов связана с площадью перекрытия их функций плотности распределения.

Ясно, что при различных средних значениях m1 и m₂ (рис. 8.3, а) вероятность ошибки убывает при увеличении расстояния между средними. Поэтому для классов с различными средними можно использовать такую меру статистической разделимости, как нормализованное расстояние:

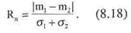
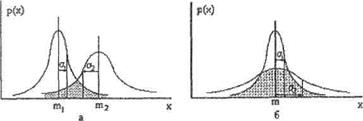
Рис.8.3. Ошибки классификации при разных средних значениях признака (а) и одинаковых средних (б).

Величина R_n связана обратной зависимостью с вероятностью ошибок: она возрастает как с увеличением расстояния между средними, так и с уменьшением дисперсии внутри классов. Для нормальных распределений эта величина принимает значение R_n=l "на уровне одного а", то есть когда функции плотности распределения соприкасаются в точках перегиба: |m1-m2l=σ₁+σ₂. На этом уровне при равных априорных вероятностях появления классов вероятность ошибок классификации (заштрихованная площадь) е=0.33. Это обычно считается верхней границей допустимой величины ошибки, то есть результат уже поддается интерпретации и постклассификационной обработке.

Для многомерного случая (при C1= C₂= С, m1≠m2) иногда используется квадратичное расстояние Махаланобиса между векторами средних значений, которое для нормальных распределений иначе называют расстоянием между плотностями распределения:

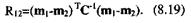
Расстояние (8.19) также обратно пропорционально ожидаемой величине ошибки.

Недостатки мер такого типа проявляются в случаях, когда средние значения для двух классов совпадают (рис.8.3, б). Поэтому для обработки всех ситуаций необходима мера более универсальная. Таковой является например, попарная дивергенция,позволяющая учесть соотношения между значениями плотностей распределения двух классов в каждой точке х.

Дивергенция определяется через так называемое среднее количество различающей информации.

Средним количеством различающей информации для класса Ω1 относительно класса Ω₂ называется величина

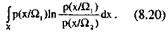
Аналогично можно записать среднее количество различающей информации для класса Ω₂ относительно класса Ω1 Тогда полное среднее количество различающей информации для пары классов Ω1 и Ω₂ будет выглядеть так:

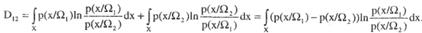
(8.21)

Величина D₁₂ называется дивергенцией. Как видно из формулы (8.21), дивергенция включает само отношение правдоподобия и его логарифм, то есть учитывает расстояние между функциями правдоподобия в каждой точке пространства X и их соотношение.

Несмотря на кажущуюся сложность выражения (8.21) для многомерного случая, для нормально распределенных значений х дивергенция достаточно просто вычисляется через средние и и ковариационные матрицы пары классов.

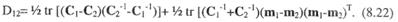
Дивергенция пригодна для оценки обеих ситуаций, представленных на

рис. 8.3. Она удовлетворяет требованиям метрики: Djj>0 при i≠j, Dij=0 при

i=j, D_ij=Dji, Dшо(х1, ..., x_n)<Dij(x,, ...,

Xn,Xn+1) то есть добавление нового

измерения никогда не приводит к уменьшению дивергенции. Более того,

если признаки классов распределены по нормальному закону с равными

ковариационными матрицами, то нетрудно показать, что Dy=Ry, где Rij -

квадратичное расстояние Махаланобиса (8.19). При статистической

независимости измерений дивергенция аддитивна: 1

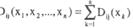
Эти свойства дивергенции иногда используют при выборе признаков для оценки их информативности [1]: при заданном количестве классов из возможного набора признаков следует отбирать те, для которых общая или средняя попарная дивергенция максимальна.

Однако квадратичная мера D с увеличением расстояния между классами растет значительно быстрее, чем величина R из (8.18). Поэтому использование для набора из К классов такой оценки, как средняя попарная дивергенция, целесообразно только в тех случаях, когда все классы распределены равномерно по пространству X. В противном случае даже один класс, далеко отстоящий от всех остальных, может дать слишком оптимистическую оценку ошибки.

В таких ситуациях предпочтительнее использовать так называемое расстояние Джеффриса-Матуситы (J-M расстояние) [4,32]. J-M расстояние рассчитывается по формуле:

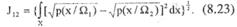
Для нормально распределенных значений признака поведение J-M расстояния связано с ожидаемой вероятностью правильного распознавания зависимостью, которую можно считать почти линейной.

В ЭРДАСЕ можно оценить качество разделения классов с помощью 4-х видов оценок, в том числе

Джеффриса-Матуситы. (см. упр. 3)

Для оценки ошибок первого и второго рода по тестовым участкам изображения при использовании конкретного классификатора (решающего правила) используется фунция Evaluate> Contingency.На выходе выдается протокол, в котором показывается сколько точек из класса k₁ попало в класс k₂ для всей совокупности классов (рис. 5).

На основании этих оценок Вы можете, как оценить качество обучающих данных, так и подобрать наиболее подходящий метод классификации. Но необходимо помнить, что полученные таким образом оценки в большинстве случаев являются слишком «оптимистичными». В результате классификации изображения ошибки могут оказаться значительно больше, хотя при удачно заданных классах всегда вполне приемлемы.

Создайте свой набор обучающих данных по тестовым участкам и проверьте их качество всеми описанными методами. Подберите наиболее удачный метод классификации для своего набора сигнатур. На тестовых участках желательно добиться 100% точности классификации.

Итоговая оценка качества автоматической классификации. Файл расстояний. Отбраковывание ненадежно классифицированных точек с помощью пороговой процедуры. Формирование матрицы итоговых ошибок классификации.

Для визуальной оценки качества классификации и отсева наиболее неудачно классифицированных точек имеется функция Threshold.Нужно открытьфайл классифицированного изображения и файл расстояний. В окне функции у Вас появится таблица, содержащая в поле Chi-Squareзначения порогов «по умолчанию». Их можно изменять. Гистограмма рассчитывается командой меню Histogram > Compute.Гистограмма расстояний аппроксимируется %² распределением (отсюда название поля Chi-Square). Если гистограмма расстояний сильно растянута и имеет пики, всего скорее, классы включают в себя несколько однородных классов. Если главная мода находится на некотором расстоянии от оси ординат, возможно смещение центра класса. Как в этом случае действовать дальше, зависит от использованной схемы классификации. Нужно еще раз проверить, соответствуют ли статистические свойства обучающих сигнатур выбранному методу классификации.

Файл расстоянийсоздаётся в процессе классификации в окне Supervised Classification включением режима Distance File.

После выполнения классификации файл расстояний можно посмотреть в отдельном вьюере. Он характеризует расстояние между вектором значений пикселя и сигнатурой класса и определяется параметрическим правилом, использованным при классификации в качестве основного или Unclassified. Для хорошего аналитика даже само растровое отображение файла расстояний может оказаться достаточно информативным.

Файл расстояний используется при так называемой «нечеткой» классификации Fazzy Classification.Этот режим формирует на выходе трехслойное изображение, в котором каждому пикселю сопоставлен трехмерный вектор «альтернативных» классов. После такой классификации можно, используя функцию Fuzzy Convolutionблока Classifier,завершить процесс классификации уже с учетом ситуации в окрестности каждого пикселя. Этот режим, однако, требует некоторых аналитических усилий и определенного опыта тематической обработки.

Пороговые расстояния можно устанавливать либо по гистограмме, либо непосредственно в таблице. Указать вюер, выбрать опцию Process > То Viewer. По умолчанию «плохо» классифицированные точки будут теперь забиты черным цветом.

Количественные оценки (матрицу ошибок) классификации можно получить с помощью функции Accuracy Assessment блока Classifier. Проще всего оценку проводить по «случайным» точкам, которые генерируются автоматически. Откройте в окне этой функции файл классификации. Затем выберите функцию View > Select Viewer и укажите исходное изображение, где Вы будете отображать точки. Классы этим точкам Вы должны будете присвоить сами. Случайные точки генерируются с помощью команды Edit > Create/Add Random Points. В окне этой команды можно отрегулировать генератор случайных чисел и число точек.

Вы можете отображать во вьюере изображения либо все точки, либо выбранные тем же способом, как и в редакторе сигнатур.

Задав все номера классов, отметьте в меню Report > Options нужные опции для отчета и затем выберите функцию Report > Accuracy Report. Вы получите отчет по оценке точности.

Учтите, что для более или менее качественной оценки требуется довольно большое количество точек (не менее ТОО в худшем случае), однако для обучения работе с процедурой при небольшом числе классов можно взять 20-30.

Методы интерактивной обработки классифицированных изображений для перехода к тематической карте. Использование функций пакета ERDAS Imagine из блока Interpreter для осуществления этого процесса.

После интерактивной обработки классифицированных изображений для перехода к тематической карте идет 1.Тематическая интерпретациязаключается в сопоставлении каждому из выделенных классов некоторой тематической категории определенной совокупности объектов земной поверхности. Здесь оцениваются реальные ошибки классификации, то есть достоверность результата. При неудачном выборе количества или описаний исходных классов может быть принято решение о повторной классификации на основе другого набора классов и системы признаков. При удовлетворительном результате выбирается схема постклассификационной обработки для перехода к тематической карте.

2. Постклассификационная обработкапредставляет собой набор интерактивных и автоматических процедур, необходимых для формирования карты объектов исследования, расклассифицированных в соответствии с тематикой задачи. К таким процедурам относятся группировка и редактирование выделенных классов, устранение обнаруженных ошибок классификации. В процессе постклассификационной обработки также могут быть использованы процедуры распознавания, в том числе структурные.

3. Подсчет количественных характеристиквключает площадные оценки по выделенным классам объектов, а также точечные оценки в соответствии с физическими моделями исследуемых процессов и явлений, оценки динамики процессов при обработке мультивременных данных и т.п. Этот этап, не имеющий прямого отношения к процессу распознавания, тем не менее, важен для его оптимизации. Накопление и анализ характеристик выделяемых классов объектов позволяет совершенствовать как саму систему распознавания, так и отдельные ее этапы.

Процесс 4.получения тематических картна основе результата обработки включает процедуры преобразования изображения к нужной картографической проекции, интерактивное редактирование результата в соответствии с точностными требованиями к картографическим материалам заданного масштаба, а также растрово-векторное преобразование при использовании векторных ГИС. Выполнение растрово-векторного преобразования требует, как правило, сглаживания результата в пределах некоторых участков для получения однородных по классам контуров. Именно с точки зрения этого этапа наиболее эффективны такие процедуры классификации, которые обеспечивают наибольшую однородность изображения по классам и наиболее четкие границы между объектами определенных тематических категорий. Если результат классификации не удовлетворяет этим условиям, процедуры сглаживания могут привести к искажению реальных границ между классами.

В блоке Interpreterвыберите пункт меню Spatial Enhancement,а в открывшемся подменю - функцию Resolution Merge.В открывшемся окне по порядку слева на право откройте файлы: 1) панхроматического изображения; 2) многозонального трансформированного вами изображения; 3) выходного результата, который Вы собираетесь получить. Режимы можете выбрать те, которые установлены по умолчанию. Нажмите ОК.