Поверки и юстировки нивелира Н3

Ориентирные углы: дирекционные, азимуты, румбы и их связь.

За первоначальные направления применяются следующие меридианы: истинные меридиан, магнитный меридиан, осевой меридиан.

Азимут географический или истинный- горизонтальный угол отсчитываемый от северного направления географического меридиана по ходу часовой стрелки до данного направления. Магнитный азимут- это горизонтальный угол, отсчитываемый от северного направления магнитного меридиана по ходу часовой стрелки до данного направления. Магнитное склонение- это угол образованный графическим и магнитным меридианом в данной точке. Дирекционный угол- горизонтальный угол отсчитываемый от северного направления осевого меридиана или линий ему параллельной по ходу часовой стрелки до данного направления. Сближение меридиана -угол образованный географическим и осевым меридианом в данной точке. Румб- острый угол отсчитываемый от ближайшего направления серидиана до данной линии.

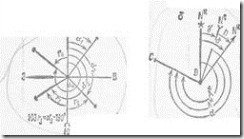
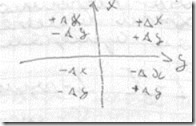
Связь дирекционного угла и румба

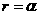- СВ 1 четверть

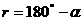-ЮВ 2 четверть

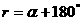-ЮЗ 3 четверть

-СЗ 4 четверть

8. Определение ориентирных углов на картах.

Ориентировать линию – значит найти её направление относительно другого направления, принимаемого за исходное. Горизонтальный угол между исходным направлением и ориентируемой линией принято называть ориентирным углом.

В качестве исходных принимают направления истинного (географического) меридиана, магнитного меридиана, осœевого меридиана, (ᴛ.ᴇ. оси Ох зональной системы прямоугольных координат либо линии, ей параллельной, проходящей через заданную точку). Учитывая зависимость отвыбранного исходного направления ориентирным углом должна быть истинный азимут А, магнитный азимут А_м, дирекционный угол α (или румб r) (рис. 3).

Истинный азимут А данного направления 1–2 – горизонтальный угол, отсчитываемый по ходу часовой стрелки от северного направления истинного меридиана, исходящего из заданной точки 1, до данного направления.

Магнитный азимут А_м данного направления 1–2 – горизонтальный угол, отсчитываемый по ходу часовой стрелки от северного направления магнитного меридиана, исходящего из заданной точки 1, до данного направления.

Дирекционный угол αданного направления 1–2 – горизонтальный угол, отсчитываемый по ходу часовой стрелки от северного направления линии, параллельной осœевому меридиану, (ᴛ.ᴇ. оси Ох), исходящей из заданной точки 1, до данного направления.

Азимуты и дирекционные углы могут изменяться от 0° до 360°.

Румб r данного направления 1–2 – острый угол, отсчитываемый от ближайшего (северного или южного) направления меридиана, исходящего из заданной точки 1, до данного направления. Румб изменяется от 0° до 90° и ᴇᴦο значение сопровождается наименованием четверти относительно сторон света.

Угол δ между направлениями истинного (С) и магнитного (С_м) меридианов принято называть склонением магнитной стрелки. Угол γмежду направлениями истинного (С) и осœевого (х) меридианов зоны (оси Ох зональной системы прямоугольных координат) принято называть сближением меридианов. Связь ориентирных углов между собой определяется выражениями˸

(6)

где – суммарная поправка.

Значения углов и для изображенного на всœем листе карты участка местности приведены в юго-западном углу листа карты; правее приводится схема взаимного расположения вертикальной линии километровой сетки (оси Ох), истинного и магнитного меридианов.

Для определœения по карте истинного азимута линии через начальную её точку, используя минутную оцифровку градусной рамки, проводят истинный меридиан, относительно которого геодезическим транспортиром измеряют с точностью до 0,1° (6') величину истинного азимута А (см. рис. 2). По истинному азимуту линии и известным значениям и рассчитывают магнитный азимут и дирекционный угол направления как

, .

Для определœения на карте дирекционного угла направления через начальную ᴇᴦο точку проводят линию, параллельную оси абсцисс, ᴛ.ᴇ. вертикальной линии километровой сетки, и относительно её измеряют транспортиром дирекционный угол (см. рис. 1). Дирекционный угол линии можно замерить в любой точке её пересечения с вертикальной линией километровой сетки. По измеренному дирекционному углу и известным значениям и рассчитывают значения истинного и магнитного азимутов по формулам˸

9. Прямая и обратная геодезические задачи.

Прямая геодезическая задача. Если известна координата начальной точки какой-то линии, дирекционный угол и горизонтальное проложение можно определить координатами конечных точек.

Дано: Xa, Ya,

Определить: Xb,Yb

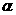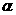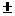
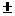
Решение: 1) X=dcos ; Y=dsin ; 3)Xb=Xa X Yb=Ya Y

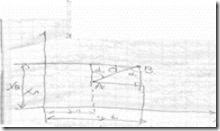
Обратная геодезическая задача.

Если известны координаты начальной и конечной точек какой-то линии, то можно определить дирекционный угол и горизонтальное проложение. Переход от румба к дирекционному углу выполняется по знакам привращений координат.

10. Виды измерений и погрешностей, свойства случайных погрешностей.

Виды измерений:

1. Прямые измерения – когда непосредственно получают уравнение с 1 мерой.

2. Косвенные измерения – когда результаты являются функцией от другой непосредственно измеряемой величины.

По точности измерения подразделяются на:

Неравноточные, когда меняется один или несколько фактов сопровождающих измерения (прибор, объект, внешние условия). Равноточные измерения, когда не меняется не один из факторов производящих измерения.

Виды погрешности:

1. Грубые погрешности, когда результаты измерений значительно отличаются от истинного значения.

2. Бывают систематические, которые возникают по конкретным причинам, по определённой математической зависимости.

3. Случайные погрешности, возникают хаотично по непонятным причинам, вне математической закономерности.

Погрешность.

Абсолютная погрешность-разность между результатом измерения и системным значением измеряемой величины. Абсолютная погрешность- это то что есть, то что должно быть. За истинное значение принимают результат получаемый теоретическим путём высокоточного измерения. Относительная погрешность- отношение абсолютной погрешности к результату измерения. Выражается всегда простой дробью с 1 в чи СВОЙСТВА СЛУЧАЙНЫХ ПОГРЕШНОСТЕЙ

В 2.1. установлено, что случайная погрешность — следствие воздействия на результат измерений множества различных по происхождению случайных факторов. Говоря о свойствах случайных погрешностей, мы имеем в виду не их индивидуальные свойства, а наиболее общие свойства, которыми обладают достаточно большие совокупности этих погрешностей.

Таких свойств четыре:

1. Свойство ограниченности. При данных условиях измерений случайная погрешность по абсолютной величине не может превзойти некоторого заранее известного предела. Этот предел называется предельной погрешностью. Обозначив ее Δ_пр, данное свойство можно выразить неравенством

|Δ|≤ Δ_пр .(2.3)

2. Свойство компенсации. Если ряд измерений одной или нескольких величин производится в одних и тех же условиях, то сумма случайных погрешностей, деленная на их число, при неограниченном увеличении ряда измерений в пределе стремится к нулю, т.е.

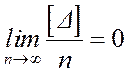. (2.4)

В выражении (2.4) и в дальнейшем мы будем употреблять символику К.Ф. Гаусса, где квадратные скобки означают сумму однородных величин. Например,

(2.5)

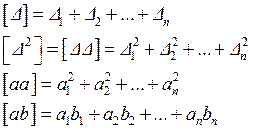
3. Свойство независимости. Если производится два ряда измерений со случайными погрешностями:

1) Δ₁^', Δ₂^',…, Δ_n^' и 2) Δ₁^'', Δ₂^'',…, Δ_n^'' ,

то сумма попарных произведений этих погрешностей, деленная на число этих произведений, при неограниченном возрастании числа измерений в пределе стремится к нулю.

Используя символику (2.5), это свойство можно записать следующим образом:

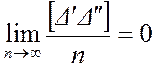. (2.6)

Заметим, что данное свойство не является всеобъемлющим. В геодезической практике не часто, но встречаются зависимые случайные погрешности.

4. Свойство рассеивания. Если ряд измерений производится в одних и тех же условиях, то для их случайных погрешностей имеет место предел

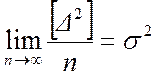. (2.7)

Величина s называется стандартом. Квадрат стандарта s² называют дисперсией, а величину

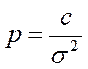, (2.8)

где c - произвольное положительное число, — весом.

Из (2.7) и (2.8) следует: ряды измерений, выполненные с более высокой точностью, обладают меньшим стандартом и дисперсией и бóльшим весом.

11. Формулы Гаусса и Бесселя, случаи их применения.

В теории погрешностей точность измерений характеризуется средней квадратической погрешностью, которая была введена знаменитым немецким математиком и геодезистом К. Ф. Гауссом (1777–1855 гг.) и обозначается через m:

m = ± √ (Δ₁² + Δ₂² + .. + Δ_n²) / n = ± √ [Δ²] / n, (4.5)

где Δ₁, Δ₂, …, Δ_n – случайные погрешности;

n – число измерений.

Средняя квадратическая погрешность является надежным критерием для оценки точности измерений. Она даже при небольшом числе измерений достаточно устойчива и хорошо отражает наличие крупных случайных ошибок, которые по существу и определяют качество измерений.

Формула (4.5) применена для вычисления средней квадратической погрешности, когда известно истинное значение измеряемой величины. Эти случаи в практике весьма редки. Как правило, истинное значение измеряемой величины неизвестно, но из измерений можно получить наиболее надежный результат – арифметическую середину. Получим формулу для вычисления средней квадратической погрешности при помощи уклонения отдельных результатов от арифметической середины по так называемым вероятнейшим погрешностям V.

Пусть l₁, l₂, …, l_n – результаты равноточных измерений одной и той же величины, истинное значение которой Х, а арифметическая середина – L. Тогда можно вычислить n случайных или истинных погрешностей

Δ_i = l_i – X (4.6)

и n вероятнейших погрешностей

V_i = l_i – L. (4.7)

Сумма n равенству (4.7)

[V] = [l] – nL. (4.8)

Но, согласно равенству (4.4) nL = [l], поэтому

[V] = 0, (4.9)

т. е. сумма вероятнейших погрешностей всегда должна быть равна нулю.

Вычитая из равенства (4.6) равенство (4.7), получим

Δ_i – V_i = L – X. (4.10)

В правой части равенству (4.10) мы имеем случайную погрешность арифметической середины. Обозначим ее через ε. Тогда

Δi = V_i + ε. (4.11)

Возведем в квадрат равенство (4.11), возьмем их сумму и разделим ее на n:

[Δ²] / n = [V²] / n + nε² / n + 2ε[V] / n. (4.12)

Левая часть этого равенства есть не что иное как m². Последнее слагаемое правой части ввиду равенства (4.9) равно нулю.

m² = [V²] / n + ε². (4.13)

Случайную погрешность ε заменим ее средним значением, т. е. средней квадратической погрешностью арифметической середины. Ниже будет доказано, что средняя квадратическая погрешность арифметической середины

М ² = ε ² = m ²/ n. (4.14)

Тогда

m ² – m² / n = [V ²] / n или m ²(n – 1) / n = [V ²] / n,

откуда ___________

m ² = [V ²] / (n – 1), или m = √ [V ²] / (n – 1). (4.15)

Формула (4.15) называется формулой Бесселя и имеет большое практическое значение. Она позволяет вычислять среднюю квадратическую погрешность по вероятнейшим уклонениям результатов измерений от арифметической средины.

Кроме средней квадратической погрешности различают еще среднюю, вероятную и относительную погрешности.

Средней погрешностью (Θ) называют среднее арифметическое из абсолютных значений случайных погрешностей т. е.

Θ = (|Δ₁| + |Δ₂| + … + |Δ_n| ) / n = [|Δ|] / n. (4.16)

В теории погрешности доказывается, что при n → ∞ Θ = 0,8 m, или m = 1,25Θ.

Иногда в прикладных вопросах пользуются вероятной погрешностью r. Вероятной погрешностью называют такое значение случайной погрешности в одном ряду равноточных измерений, по отношению к которой одинаково возможна погрешность как больше, так и меньше этого значения, по абсолютной величине. Для нахождения r все погрешности данного ряда располагают в порядке возрастания по абсолютной величине и выбирают то значение, которое занимает среднее положение, т. е. погрешностей меньше его столько же, сколько и больше. Вероятная погрешность связана со средней квадратической погрешностью соотношением r = 2/3 m = 0,67 m или m = 1,5 r.

Как видно, m > Θ и m > r, что показывает, что средняя квадратическая погрешность лучше характеризует точность измерений, чем средняя и вероятная погрешности.

Оценку точности таких измеренных величин, как линии, площади и объемы часто производят с помощью относительной погрешности. Относительной погрешностью называют отношение абсолютной погрешности к значению измеренной величины. Относительная погрешность записывается в виде дроби, в числителе которой стоит единица, а в знаменателе – число, показывающее какую долю измеряемой величины должна составлять допустимая погрешность. Например, длина стороны D = 150 м измерена с абсолютной погрешностью m_d = 0,05 м. Тогда относительная погрешность результата измерения составит m_d / D = 0,05 м / 150 м = 1 / 3000.

Величина 1 / 3000 означает, что на 3000 м расстояния может быть допущена погрешность в 1 м. Чем больше знаменатель относительной погрешности, тем выше точность измерений. Точность всех линейных измерений в геодезии всегда задается относительной погрешностью, которая приводится в соответствующих инструкциях и наставлениях по производству данного вида геодезических работ.

12. Теодолит, классификация, назначение, устройство.

Теодолит предназначен для измерения горизонтальных и вертикальных углов для измерения расстояний для измерения ориентирных углов. Приборы у которых горизонтальные и вертикальные круги выполнены из высокоточного стекла относятся к оптическим теодолитам. По точности теодолиты подразделяются:

1) высокоточные Т-1

2) точные Т2 и Т5

3) технические Т15, Т30

4) учебные Т60

Цифра после буквы означает среднеквадратичную погрешность измерения угла в секунду полным приёмом. По устройству теодолиты подразделяют на прямые и обратные. С цилиндрическим уровнем и с компенсатором- это устройство внутри прибора позволяющее автоматически приводить ось прибора в отвесное положение.

Основные части теодолита.

1) Зрительная труба: объектив, окуляр, сетка нитей, линза.

Линия проходящая через центр окуляра и центр объектива называется оптическая ось. Визирная ось-линия проходящая через центр объектива и центр сетки нитей.

Характеристики зрительной трубы.

Увеличение. Полезрение, то пространство которое видно в зрительную трубу при неподвижном её положении. Освещённость.

2) Горизонтальный круг выполняется из высокоточного стекла и он поделён на градусы.

Вертикальная ось прибора –линия проходящая через центр алидады либо ось вращения теодолита.

3)Вертикальный круг состоит из лимба и алидады. Уровень предназначен для приведения прибора в рабочее положение. Ось цилиндрического уровня- касательная линия внутри поверхности уровня в нуль пункт.

Свойство цилиндрического уровня.

Когда пузырёк находится в ноль пункте, ось уровня занимает горизонтальное положение. Центр деления угол отклонения от горизонтального положения при смещения пузырька на 1 деление. Существуют штриховые микроскопы, шкаловой микроскоп, оптический микроскоп, микроскоп-микрометр.

Основные оси теодолита:

Вертикальная ось(ось вращения),ось цилиндрического уровня, горизонтальная (ось вращения зрительной трубы), визирная ось зрительной трубы.

13. Устройство и поверки теодолита 2Т3О.

1. Поверка: ось цилиндрического уровня при горизонтальном круге должна быть перпендикулярна вертикальной оси прибора.

2. Поверка: горизонтальный штрих сетки нитей должен быть перпендикулярен вертикальной оси прибора (юстировочные винты).

3. Поверка: визирная ось зрительной трубы должна быть перпендикулярна горизонтальной оси прибора. КЛ и КП- отсчёты по горизонтальному кругу. С-коммационная погрешность. С=(КЛ-КП-+180)/2=1градусу или меньше.

Юстировка:

1. Nпр=КЛ-С

2.устанавливаем правильный отсчет на микроскопе при помощи наводящего винта алидады.

3. Возвращаем сетку нитей центром на точку при помощи юстировочных винтов.

14. Принцип и способы измерения горизонтальных углов.

Способ полуприёма:

Отличается простотой самый быстрый способ и не имеет контроля. Теодолит устанавливается в вершину горизонтального угла и приводят в рабочее положение.

1. Центрирование- совмещение вертикальной оси прибора с вершиной измеряемого угла, выполняется с помощью нитяного отвеса.

2. Горизонтирование- приведение вертикальной оси прибора в отвесное положение (уровень). Лимб горизонтального круга при измерении закрепляют.

Вывод: способ полуприёма применяется при теодолитной съёмке и тахеометрической.

Способ приёма (полный приём).

Состоит из двух полуприёмов, т.е угол измеряется дважды при двух положениях вертикального круга:

1-ый полуприём КП

B1=а прт-в левт

2-ой полуприём КЛ

B2=а прт – в левт

Контроль сравнение: В1-В2<=2t; t-точность. Вср=(В1+В2)/2- свободна от влияния коммационной погрешности.

Существуют ещё способы круговых приёмов, повторений, комбинаций.

15. Измерение вертикальных углов.

Для измерения вертикальных углов служит вертикальный круг теодолита, жестко укрепленный на оси зрительной трубы и вращающийся вместе с ней.

В точных теодолитах соосно с вертикальным кругом крепится алидада вертикального круга с отсчетным устройством и собственным уровнем или компенсатором углов наклона, его заменяющим.

В теодолитах Т30 отсчетное устройство вертикального круга укреплено неподвижно в стойке теодолита, а его уровнем служит уровень при алидаде горизонтального круга. При измерении вертикального угла пузырек уровня приводят в нульпункт подъемными винтами подставки.

Вертикальные круги разных типов теодолитов оцифрованы различно, отчего различаются формулы вычисления вертикальных углов по полученным в ходе измерений отсчетам. Рассмотрим измерение углов наклона теодолитом Т30.

Отсчет при трубе, расположенной горизонтально, и пузырьке уровня в нульпункте называется местом нуля вертикального круга (М0).

Для измерения вертикального угла наводят трубу на визирную цель при двух положениях вертикального круга (слева и справа) и, приводя каждый раз пузырек уровня в нульпункт, берут отсчеты по вертикальному кругу: Л (лево) и П (право).

Очевидно, что угол наклона равен разности отсчетов при трубе, наведенной на цель и при трубе, расположенной горизонтально. Поэтому для круга слева напишем

ν = Л – М0. (7.1)

Аналогично, учитывая оцифровку вертикального круга Т30, где при круге справа отсчеты сопровождаются противоположным знаком (положительные углы знаком минус и наоборот), напишем

ν = М0 – П (7.2)

Из формул (7.1) и (7.2) находим формулы угла наклона и места нуля.

;

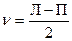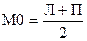. (7.3).

В ряде случаев, определяя углы наклона, ограничиваются измерениями при одном положении вертикального круга (слева или справа). Тогда пользуются формулой (7.1) или (7.2), для чего предварительно необходимо определить место нуля, измерив какой-нибудь угол при двух положениях вертикального круга и вычислив место нуля по формуле (7.3).

Вычисления по формулам (7.1) - (7.2) упрощаются, когда М0=0. Поэтому, если место нуля велико, его исправляют. При круге слева и пузырьке уровня в нульпункте наводят трубу на точку, по которой определяли место нуля. Вращением наводящего винта трубы устанавливают на вертикальном круге отсчет, равный углу наклона n. При этом изображение точки сместится из центра сетки нитей. Действуя вертикальными исправительными винтами сетки нитей, смещают сетку так, чтобы изображение точки оказалось в центре сетки. Учитывая что теперь труба наведена на точку с углом наклона n, и отсчет по вертикальному кругу равен Л = n из равенства (7.1) видим, что место нуля стало равно нулю М0 = 0.

16. Измерение углов наклона сторон теодолитного хода.

17. Устройство и поверки нивелира Н-3.

Нивелир- это геодезический прибор, с помощью которого определяют превышение между точками. Нивелиры в зависимости от их конструкции бывают с цилиндрическим уровнем (уровненные нивелиры) и с компенсатором. В первом случае горизонтальность визирного луча определяется с помощью уровня, а во втором с помощью компенсатора. К названию нивелира также могут добавляться буквы К и Л, а перед буквой Н могут стоять цифры, обозначающие номер модели модификации прибора. Например: 2Н-10КЛ означает: вторая модификация нивелира Н10 с компенсатором и лимбом. В настоящее время широко используют нивелиры Н-3, Н-3К, Н-3КЛ, Н-10Л и др.

Нивелир Н-3:

Основными частями нивелира являются: подставка7 снабжённая подъёмочными винтами8, элевационный винт6, зрительная труба5, цилиндрический уровень4. Наводя

щий винт3, круглый уровень1, закрепительный винт2.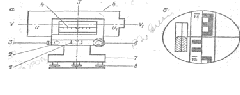

Основные оси нивелира: ось вращения прибора, визирная ось зрительной трубы. Для наведения прибора на рейки используют закрепительные и наводящие винты. Круглый винт служит для приведения прибора в отвесное положение.

Классификация нивелиров: Высокоточные Н-0.5, точные нивелиры Н-3, технические нивелирыН-10

Поверки и юстировки нивелира Н3

Эльвационный винт предназначен для приведения пузырька цилиндрического уровня в ноль пункт.

1. Поверка: ось круглого уровня должна быть параллельна вертикальной оси прибора.

2. Поверка: вертикальный штрих сетки должен быть параллелен вертикальной оси прибора.

3. Поверка (нитяной отвес): главная визирная ось зрительной трубы должна быть параллельна оси цилиндрического уровня.

X=(a+b)/2-(Iпра + iпрв)/2=<4

Юстировка:

1. Nпр=a-x

2. Устанавливают правильный отсчёт эливационным винтом.

3. Возвращают пузырёк цилиндрического уровня в ноль пункт, юстировочным винтом.

18. Виды нивелирования. Способы геометрического нивелирования.

Нивелирование- это вид геодезических работ по определению превышений. Нивелирование обычно используют для определения высот точек при составлении топографических планов, карт, профилей, при перенесении проектов застройки и планировки территорий по высоте. Различают следующие методы нивелирования: геометрическое, Тригонометрическое, физическое и автоматическое.

Геометрическое нивелирование-метод определения превышения с помощью горизонтального визирного луча и нивелирных реек. Для получения горизонтального луча используют нивелир. Широко применяется в строительстве.

Тригонометрическое нивелирование- это метод определения превышения по измеренному углу наклона и расстояния между точками. Его применяют при топографических съёмках и при определении больших превышений.

Физическое нивелирование относятся методы: гидростатического нивелирования, основанный на применении сообщающихся сосудов, барометрическое нивелирование, разность давлений, радиолокационное нивелирование, основанный на отражении электромагнитных волн от земной поверхности.

Автоматическое нивелирование, осуществляется с помощью специальных приборов устанавливаемых на авто. Сразу вычерчивается профиль местности на ленте.

Геометрическое нивелирование:

1. При нивелировании из середины. В точках А и В устанавливают отвесно рейки. На которых нанесены шкалы, а по середине нивелир. Когда осуществляют нивелирование от А к В то рейку в точке А считают задней а В передней. Если взять отсчёты а и в то превышение будет равно h=a-b

2. При нивелировании вперёд нивелир устанавливают в точке А, измеряют высоту прибора I а затем берут отсчёт b. Превышение вычисляется по формуле h=i-b

После определения высоты точек находят: Нв=На+h. Когда высоты точек расположены на значительном расстоянии. В этом случае от точки А до В прокладывают нивелирный ход, состоящий из нескольких станций. Превышение между точками будет равно сумме превышений hав. Высоту точки В находят по формуле Нв=На+ hав

19. Определение отметок через горизонт прибора.

Чтобы определить отметку точки через горизонт инструмента необходимо от горизонта инструмента отнять чёрный отсчёт этой точки.

20. Линейные измерения: приборы, последовательность измерения.

Приборы для непосредственных измерений:

1. Землемерная лента А3-20, А3-50

2. Шкаловая землемерная лента. На кончиках есть сантиметровые деления и метровые.

ЛЗШ-20, ЛЗШ-50

3. Рулетки (металлические, на основе стекловолокна, пластик)

4. Инварная проволка

Компарирование- определение действительной длины мерного прибора путём сравнения с эталоном. Компараторы- отрезок закреплённый на местности или в помещении. Длина которого измеряется с высокой точностью. L=Lэт-Lпр

Порядок линейных измерений:

1. Закрепление точек.

2. Вещение линий- установка дополнительных вешек в створе измерений линий.

3. Измерение расстояний в прямом и обратном направлении.

Д=Lпр*n+r, где n-количество уложений прибора; r-остаток.

Дср=Дпр/2+Добр/2

Оценка точности сделанных измерений . Точность оценивается относительной погрешностью. =Дср-Добр –абсолютная погрешность

fотн= /Дср=1/N

Допускаются относительные погрешности:

1. ЛЗ 1/1000 1/3000; 2. ЛЗЩ, РУЛ 1/3000 1/10000; 3 инварная проволка 1/100; 4. светодальномер 1/107.

21. Оценка точности линейных измерений, введение поправок.

Измерение линий стальной лентой производится двумя исполнителями. Один из них находится в начальной точке линии и называется задним мерщиком, другой – передним.

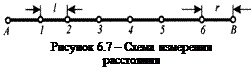Для измерения линии АВ (рисунок 6.7) ленту разматывают и укладывают вдоль линии. Из шести шпилек передний мерщик берет себе пять, оставляя шестую заднему. Задний мерщик втыкает шпильку в землю рядом с колышком, обозначающим начало А измеряемой линии, и зацепляет за нее конец ленты. Ориентируясь выставленными на линии вехами, направляет переднего мерщика так, чтобы лента легла в створе линии АВ. Передний мерщик, встряхнув ленту, натягивает ее и через вырез в конце ленты вертикально ставит первую шпильку, прочно воткнув ее в землю (точка 1). Оставив шпильку в точке 1, передний мерщик протягивает ленту вперед по линии, пока задний не дойдет до этой шпильки. Подобно предыдущему, от точки 1 откладывают ленту второй раз, и передний мерщик выставляет на линии вторую шпильку в точке 2. Затем задний мерщик вынимает первую и берет ее с собой, а передний оставляет шпильку в точке 2 и протягивает ленту вперед и т. д. Дойдя до точки В, передний мерщик протягивает ленту дальше по продолжению линии, после чего по ленте отсчитывается длина остатка r (отрезок 6 –В). По окончании измерения подсчитывают шпильки у заднего мерщика, и по их количеству определяют число уложенных лент. В данном примере их было шесть. Если длина ленты 20 м и остаток оказался равным, например, 7,84 м, то вся длина линии АВ будет 20 ∙ 6 + 7,84 = 127,84 м.

Измеренные расстояния при необходимости исправляют поправками за компарирование ленты и за отклонение температуры воздуха от температуры в момент компарирования. Общая длина линии АВ вычисляется по формуле

D = nl₀ + r + nΔl_к + ΔD_t,

где n – число уложений мерного прибора;

l_o – номинальная длина мерного прибора;

r – остаток, часть мерного прибора при его последнем укладывании;

Δl_к – поправка за компарирование мерной ленты;

ΔD_t – поправка за температуру.

Поправка за температуру

ΔD_t = G (t – t₀) D,

где G – коэффициент линейного расширения материала мерного прибора

(например, для стальной рулетки G = 12,5∙10^{-6 м / град);}

t – температура мерного прибора во время измерения;

t₀ – температура при которой проводилось компарирование.

При разности температур (t – t₀) < 8^о поправка за температуру не учитывается.

Для контроля и повышения точности результатов измерений каждую линию измеряют минимум два раза в прямом и обратном направлениях. При измерении линий лентой обычным способом расхождения между результатами двух измерений не должны превышать: 1:2000 измеренной длины – при благоприятных условиях для измерений, 1:1500 – при средних условиях измерений и 1:1000 – при неблагоприятных условиях (пересеченная местность, болото, песок и т. д.). Если расхождение между результатами двух измерений допустимо, то за окончательную длину линии принимают среднее арифметическое из двух значений.

22. Измерение расстояний нитяным дальномером при горизонтальном положении визирной оси.

23.Измерение расстояний нитяным дальномером при наклонном положении визирной оси.

Принцип измерения расстояний дальномерами основан на решении прямоугольного треугольника, в котором по малому параллактическому углу и противолежащему катету Наибольшее распространение в геодезической прак­тике нашел нитяный дальномер. Это дальномер с постоян­ным параллактическим углом и переменным базисом. Он состоит из двух горизонтальных нитей, параллельных средней нити сетки трубы прибора. В комплект дально­мера входит вертикальная рейка с сантиметровыми деле­ниями.

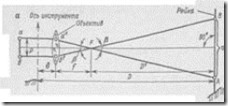
Для измерения расстояний на одном конце отрезка устанавливают прибор, а на другом — рейку (рис. 36, а). Пусть визирная ось трубы горизонтальна. Лучи от дальномерных нитей, изображенных на рисунке точками а и b,пройдя через объектив и передний фокус F, пересе­кут рейку в точках A и В. Из подобия треугольников AFB и a’Fb’ : D'/n = f/p,откуда

D’=(f/p)n где f — фокусное расстояние объектива; р — расстояние между дальномерными нитями.

Отношение f/p = К для данного прибора постоянно и называется коэффициентом дальномера. На рис. 36, а видно, что

D = D' + f+ 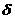где б — расстояние от объектива до оси вращения трубы.

Величину с = f + б называют постоянным слагаемым дальномера, а определямое расстояние вычисляют по формуле D = Кп + с. (50)

В современных приборах постоянное слагаемое мало и его часто не учитывают при измерениях.

В приборах с фокусным расстоянием объектива / = = 200 мм обычно расстояние между далъномерными ни­тями делают равным р = 2 мм. В этом случае К = f/p = 100, что существенно упрощает вычисления. При сан­тиметровых делениях рейки дальномерный отсчет по ней в делениях выразит расстояние в метрах.

Формула (50) получена для случая, когда рейка рас­положена перпендикулярно к визирной оситрубы. При измерениях на местности это условие нарушается, так как рейку устанавливают вертикально и при наклонном по­ложении визирной оси (рис. 36, б). Если рейка наклонена по отношению к визирной оси на угол v, то вместо пра­вильного отсчетаM'N' = п' возьмут отсчет MN = n. Эти величины связаны соотношением п’ = п cos v. Подставляя значение п! в формулу (50), получим D = Кп' + е= Кп cos v + с.

Но d = D cos v, тогда d = Кп cos² v + с cos v.

Величины с и v малы, поэтому с cos v 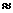с cos² v, тогда d 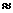(Кп + с) cos² v. (51)

Для вычислений горизонтальных проложений более удобно воспользоваться поправками

D_V = d - D 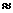D (1 — cos² v) 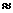D sin² v.

24. Тригонометрическое нивелирование.

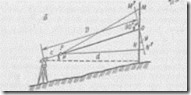
При тригонометрическом нивелировании (рис. 49) над точкой А устанавливают теодолит и измеряют высоту при­ора i а в точке В устанавливают рейки. Для определения превышения h измеряют угол наклона v, горизонтальное проложение d и фиксируют высоту визирования v отсчет, на который наведен визирный луч). Из рис. 49 видно, что

В1В2= d tg v; В1В3=В1В2+I;

H=ВВ3=В1В-v; тогда h= d tg v+i-v

При использовании тригонометрического нивелирова­ния для топографических съемок в качестве визирной цели в точке В устанавливают нивелирную рейку. В этом случае dопределяют с помощью нитяного дальномера.

Известно, что d=(Kn =с) cos² v. Подставив это значение в (146), получим формулу для вычисления превышения:

h = (Кп + с) cos² v tg v + i-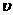

h =(1/2) (Кп + c) sin² v + i-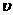

В процессу нивелирования на открытой местности при измерении угла v удобно визировать на точку, располо­женную на высоте прибора. Для этого на отсчете по рейке, равном iпривязы­вают ленту. Тогда при i_n = v формула (147) примет вид

h = (1/2) (Кп + с) sin 2v. Для получения средней квадратической погрешности тригонометрического нивелирования найдем частные про­изводные (79):

dh/dd= tg v; dh/dv=d/cos² v; dh/di_n=1; dh/dv=1;

Подставляя частные производные и значения средних квадратических погрешностей измеренных элементов в формулу (17), получаем

m_h:^2=m_d^2 tg v+d^2/ cos⁴ v * m²_v/ p^2+ m_i ^2+ m_v ^2

где m_h — средняя квадратическая погрешность определе­ния превышений тригонометрическим нивелированием. Обычно m_i и m_v бывают меньше 1 см и ими в расчётах точности можно пренебречь. При углах |v| <=5 можно принять tg v = v/p, cos v = 1. С учетом этот формула (79) примет следующий вид

m_h:^2=(v^2m_d^2+d²m²_v)(1/р²)

25. Понятие о съемках и съемочном обосновании.

Съёмочное обоснование создаётся на основе общего принципа построения геодезических сетей- от общего к частному. Оно опирается на пункты государственной сети и сетей сгущения, погрешности которых пренебрегаемо малы по сравнению с погрешностями съёмочного обоснования. Точность создания обоснования обеспечивает проведение топографических съёмок с погрешностями в пределах графической точности построений на плане данного масштаба.

Наиболее часто в качестве планового обоснования используют теодолитные ходы. На открытой местности теодолитные ходы иногда заменяют рядами или сетью микротриангуляции, а на застроенной территории- сетями из четырёх угольников без диагоналей.

Высотное обоснование обычно создаётся в виде сетей нивелирования 4 класса или технического нивелирования. Получают редкую сеть пунктов, которая в последующем сгущается высотными ходами. В этих ходах превышения определяют тригонометрическим способом.

26. Создание планового съемочного обоснования.

27.Создание высотного съемочного обоснования.

Для выполнения топографо – геодезических работ на объекте (закрепления межевых знаков, составления и обновления карт масштаба 1: 5000, определения границ и площадей земельного участка) создается планово-высотное обоснование.

Создание планово – высотного обоснования выполняется в соответствии с инструкцией ГКНТА – 2.04 – 02 – 98.

Точки планово – высотного обоснование и межевые знаки границ населенного пункта определяются с точностью не ниже полигонометрии 2 разряда (относительная точность 1:5000) и технического нивелирования (50v-L мм).

Закрепление точек планово – высотного обоснования производится центрами типа У 15Н на незастроенной территории, на застроенной территории центрами У 15 (см приложение 5) и марками в бетоне (см. приложение 6).

Закрепление межевых знаков соответствует закреплению пунктов полигонометрии.

При последующем выполнении топографо – геодезических работ межевые знаки могут использоваться как исходные пункты полигонометрии для развития съемочной сети.

Планово – высотное обоснование создается при помощи GPS системы устройством ProMark3.

ProMark3 – это устройство сбора данных для проведения работ, связанных с проведением съемки ГИС - проектов. Кроме того, оно включает полный набор навигационных функций. ProMark3 имеет большой экран с высоким разрешением и предлагает улучшенную связь через Bluetooth, USB и последовательное соединение.

При разбивки планово – высотного обоснования устройством ProMark3 базовая станция приемника размещается на точке с известными координатами (пункты ГГС, полигонометрии, триангуляции), а второй приемник, ровер, размещается на точке координаты которой необходимо вычислить. Оба приемника работают в режиме статической съемки (рис 4. Cхема расположения приемников GPS)

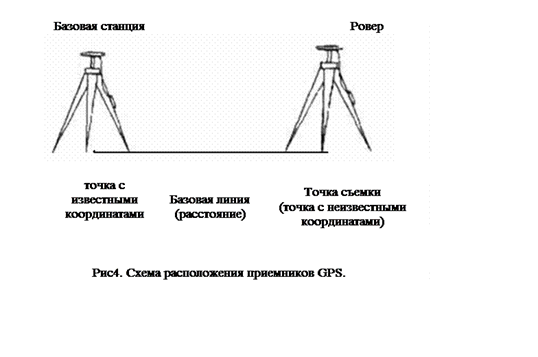При таком методе определения координат точек планово - высотного обоснования необходимо выполнить контрольные измерения, что позволит повысить точность при камеральной обработке. Для этого приемник ровера надо установить на двух – трех точках с известными координатами.

28. Теодолитная съемка, способы съемки.

1) Способ прямоугольных координат для твёрдых тел. Из характерных точек опускается перпендикуляр на стороны теодолитного хода (на глаз). Координаты X и Y измеряются рулетками и землемерными лентами. Результаты заносятся в абрис. На плане координаты

X и Y откладывают в соответственном масштабе.

2)Полимерный способ. Выполняется теодолитом с нивелирной рейкой. В характерной точке устанавливают рейку, снимают отсчёты по ГК и дальномерные. Все результаты измерения заносят в абрис.

3)Способ линейных засечек. Выполняется для точек расположенных не далеко от съёмочного обоснования. С помощью линейных измерений. Расстояния должны быть приблизительно равны. Определяются точки на плане. Определяется пересечение дуг окружности с радиусом L1 L3выражаемых в масштабе.

4) Способ угловых засечек. Применяется для удалённых точек. Выполняются с помощью теодолита, который устанавливается в точке съёмочного обоснования. На станции выполняется ориентирование прибора. Трубу наводят на точку и снимают отсчёты по ГК.

5)Способ створа для привязки. В основном линейных сооружений. Способ створа выполняется с помощью измерения расстояния до линейного сооружения вдоль сторон теодолитного кода.

29. Тахеометрическая съёмка.

Тахеометрическую съёмку предметов, контуров местности производят полярным методом, а отметки точек определяют тригонометрическим нивелированием. Все измерения выполняют при одном наведении зрительной трубы на рейку.

1) Устанавливают теодолит над точкой съёмочного обоснования и приводят в рабочее положение затем измеряют высоту прибора.

2) Определение места нуля

3) Ориентируем лимп по направлению на одну из точек съёмочного обоснования т.к все последующие измерения на станции будут выполнятся при одном положении вертикального круга то ориентирование теодолита осуществляется при положении круга лева, при этом совмещают отчетный индекс алидады с нулевым штрихом лимба горизонтального круга. Закрепляем алидаду и вращая лимп визируем на выбранную точку съёмочного обоснования. После этого закрепляем лимп. В данном положении для измерения углов на станции достаточно открепить алидаду, навести зрительную трубу на рейку и взять отсчёт по ГК.

4) На каждой станции выявляют характерные точки ситуации и рельефа. Составляем абрис. При съёмке рельефа реечные точки располагают на характерных для рельефа формах. Их распределяют равномерно.

5) Последовательно устанавливают рейку на все намеченные точки, отсчёты берут в следующей последовательности: по дальномеру, по ВК, по ГК. Результаты записывают в тахеометрический журнал.

6) По окончании работ на станции для контроля вновь визируют на начальную точку. Расхождение с начальными данными не должно превышать 3 минуты.

30. Государственные геодезические сети.

Геодезическая сеть-совокупность точек закреплённых на местности специальными знаками, положение которых определяется в единой систем координат. Точки относящиеся к геодезической сети называют геодезическими пунктами.

Виды геодезических сетей:

1) Государственные геодезические сети- главные сети, имеют большую протяжённость ими покрыта вся территория страны. Предназначены: являются основой для построения низших сетей, для решения научных задач.

2) Сети сгущения: предназначены для увеличения плотности пунктов на 1 площади.

3) Сети съёмочного обоснования на основе которых непосредственно производятся съёмки контуров и рельефа местности, инженерно-геодезические работы при строительстве сооружений.

4) Специальные сети, развиваемые при строительстве сооружений, представляющих к геодезическим работам специальные требования.

Геодезические сети подразделяются на плановые и высотные. Плановые сети служат для определения плановых координат геодезических пунктах ХиY. Высотные для определения высот пунктов H. Геодезические пункты закреплены на местности по разному временными и постоянными значками.

Плановые и геодезические сети. Пункты ГГС закреплены постоянными значками и СС. Это подземная конструкция, которая выполнена из монолитного бетона и заглублена ниже глубины промерзания.