Печатается по решению редакционно-издательского совета Вятского государственного университет

Вятский государственный университет

Факультет строительства и архитектуры

Кафедра "Строительное производство"

С.М. Чернявский

работа с топографическими планшетами

Методические указания к лабораторным работам

	для специальностей:270102 ПГС, 270105 ГСХ

Киров 2008

Печатается по решению редакционно-издательского совета Вятского государственного университет

УДК 528.48(07)

Рецензент: Заслуженный строитель России, доцент, директор ЗАО “Кировагропромпроект”, К.В. Подкопаевский

Редактор Е.Г. Козвонина

Компьютерная вёрстка автора

Подписано в печать Усл. печ. л. 4,25

Бумага офсетная. Печать матричная

Заказ № Тираж Бесплатно

Текст напечатан с оригинала - макета, представленного автором.

610000, г. Киров, ул. Московская, 36

Оформление обложки, изготовление – ПРИП ВятГУ.

© С.М. Чернявский 2008

© Вятский государственный университет,2008

оглавление

i. масштабы топографических карт и планов, поперечный

масштаб 4

ii. определение площадей планиметром 9

iii. номенклатура листов карт и планов 17

IV. РЕШЕНИЕ ЗАДАЧ НА ТОПОГРАФИЧЕСКОМ ПЛАНШЕТЕ 27

IV.1. РАЗГРАФКА РАМОК ТОПОГРАФИЧЕСКИХ КАРТ. 27

IV.2. ОПРЕДЕЛЕНИЕ ПРЯМОУГОЛЬНЫХ КООРДИНАТ ТОЧКИ 29

IV.3. ОПРЕДЕЛЕНИЕ ДИРЕКЦИОННОГО УГЛА НАПРАВЛЕНИЯ С

ТОЧКИ НА ТОЧКУ 29

IV.4. ОПРЕДЕЛЕНИЕ ВЫСОТНОЙ ОТМЕТКИ ТОЧКИ 30

IV.5.ПОСТРОЕНИЕ ПРОФИЛЯ МЕСТНОСТИ НА ЗАДАННОМ

ОТРЕЗКЕ 31

IV.6. ОПРЕДЕЛЕНИЕ КРУТИЗНЫ СКАТА 31

IV.7. ТРАССИРОВАНИЕ С ЗАДАННЫМ УКЛОНОМ 31

IV.8. ПОЛУЧЕНИЕ НА ПЛАНШЕТЕ ГРАНИЦ ВОДОСБОРНОЙ

ПЛОЩАДИ. 32

Литература 34

I. масштабы топографических карт и планов, поперечный масштаб

ЧИСЛОВОИ МАСШТАБ. План и карта являются уменьшенными изображениями на горизонтальной плоскости участков земной поверхности с их искуственными и естественными объектами. Степень этого уменьшения называют масштабом. Отношение единицы длины взятой в виде отрезка на плане или карте к числу таких же единиц, содержащихся в соответствующем горизонтальном отрезке в натуре называют числовым масштабом данного плана или карты.

Для топографических планов приняты следующие масштабы:

1: 500; 1: 1000; 1: 2000; 1: 5000.

Для топографических карт:

1: 5000; 1: 10000; 1: 25000; 1: 50000; 1: 100000;-крупномасштабные

1:100000; 1: 200000; 1: 500000;1: 1000000 - среднемасштабные.

Из всех перечисленных масштабов самым крупным является 1: 500, а самым мелким – 1: 1000000. Более мелкие масштабы применяются для географических карт. По признаку последовательности все приведенные масштабы называют масштабным рядом.

линейный масштаб – графическое изображение числового масштаба, приспособленное для перевода длин отрезков с плана в натуру и наоборот. На всех планах и картах приводятся оба масштаба – числовой и линейный, соответствующие один другому. На рис.1 изображены линейные масштабы, соответствующие числовым 1: 10000 и 1: 25000. Интервалы, на которые разделяют по длине линейный масштаб, называют его основаниями. Основания принимают равными 1, 2, 4, или 5 сантиметров в зависимости от числового масштаба планшета. Крайнее левое основание разбивают на более мелкие деления. Это помогает работать с масштабом без наличия линейки, а также при измерении отрезков небольших длин.

Рис. 1

точность масштаба. Так называют длину отрезка в натуре, соответствующую 0,1 мм на плане (карте). Практикой установлено. что предельное малое расстояние между точками, которое можно рассмотреть невооруженным глазом на плане (карте), равно 0,1 мм. Если возникает вопрос о том, в каком масштабе нужно построить план, чтобы на нем можно было отобразить отрезки в натуре длиной 0,5 м, то эти 0,5 м принимают за точность масштаба. Длина 0,5 м в натуре соответствуют 0,1 мм на плане, а значит 1мм на плане должен соответствовать 5 м или 5000 мм. Искомый масштаб для построения плана будет 1:5000.

Значения точности масштаба для карт масштабов 1:10000; 1:25000; 1:50000 равны соответственно – 1 м; 2,5 м; 5 м; и т. д.

поперечный масштаб. Выдержать точность масштаба при построении плана (карты) и при работе с ними без использования специальных средств практически невозможно. Таким специальным средством является поперечный масштаб. В промышленном исполнении (рис.2) он представляет собой металлическую пластину с 11-ю продольными (горизонтальными) параллельными линиями через интервалы в 3 мм, с рядом поперечных (вертикальных) линий через интервалы в 20 мм и с 10-ю кососекущими линиями, проведенными через интервалы в 2 мм в левом интервале между вертикальными линиями. Длину интервала между вертикальными линиями называют основанием поперечного масштаба и принимают всегда в 20 мм.

Рис. 2

При необходимости поперечный масштаб аккуратно вычерчивают на плотной чертежной бумаге тушью тонкими линиями. Вычерчивание выполняют в следующем порядке:

На равных расстаяниях проводят 11 горизонтальных линий. Делят их вертикальными линиями на интервалы в 2 см. Из точки К под произвольным углом к горизонтальным линиям проводят прямую, на которой циркулем-измерителем разбивают 10 равных отрезков произвольной длины и получают точку L. Через концы этих отрезков проводят прямые, параллельные отрезку LО. При этом отрезок КО автоматически делится на десять равных частей (интервалов), каждая из которых равна 0,1 основания, то есть два мм.

Через полученную от такого деления точку 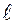и точку 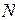продят прямую, параллельно которой через концы других делений на интервале КO проводят и другие кососекущие прямые. Отрезки горизонтальных прямых, заключенные в треугольнике 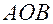изменяют свою длину от нуля до 2 мм. С каждым новым интервалом между горизонтальными прямыми эти отрезки изменяют свою длину на на 0,01 основания или на 0,2 мм (2:10=0,2). Так отрезок ef , поднимаясь на 4 интервала между горизонталями и становясь отрезком cd увеличивает свою длину на 0,2 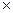4=0,8 мм и становится равным 1 мм.

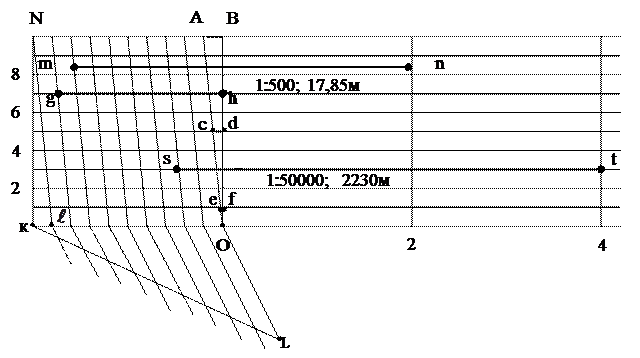
Рис. 3

После построений линии поперечного масштаба оцифровывают, как это показано на рис. 3

пользованием поперечным масштабом.

Один и тот же поперечный масштаб одинаково успешно используется при любом масштабе плана (карты).

Предположим, что на карте масштаба 1: 50000 требуется определить расстояние между точками s и t в натуре. Основание поперечного масштаба в этом случае равно тысяче метров на местности. Интервал составит сто метров, а приращение при подъёме на одну горизонталь будет равно десяти метрам.

Циркулем-измерителем измеряют расстояние на карте и переносят его на поперечный масштаб таким образом, чтобы одна из иголок циркуля пришлась на вертикальную линию, а другая - на кососекущую и чтобы створ иголок располагался параллельно горизонтальным линиям.

Как показано на рисунке 3, в раствор циркуля st умещается два основания, два интервала и приращение в виде отрезка на 3-й горизонтальной линии. Отсюда, расстояние между точками s и t на карте составляет: 2х1000 м+2х100 м+3х10 м = 2230 м.

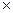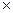Это же расстояние можно посчитать другим методом: 20 2+2 2+0,2 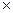3=44,6 мм. Согласно приведенному масштабу карты 1 мм соответствует в натуре 50000 мм или 50 м. И при таком подсчете расстояние s t равно 50 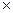44, 6= 2230 м.

Еще один подобный пример: По плану масштаба 1: 500 требуется определить расстояние в натуре между точками m и n. В этом примере основание на местности равно десяти метрам, интервал – одному метру, а приращение при подъёме на одну горизонталь составит десять сантиметров.

Раствор циркуля-измерителя включает в себя одно основание (20 мм), семь интервалов (2 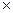7=14 мм) и приращение при подъёме циркуля на восемь с половиной горизонталей (0,2 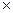8,5=1,7 мм). Следовательно расстояние между точками на местности (в натуре) равно: 1х10+7х1+8,5х0,1=17,85 м. Или по другойметодике: раствор циркуля составляет 20+14+1,7=35,7 мм. Согласно масштабу 1: 500 плана 1 мм соответствует 500 мм или 0,5 м. Значит, отрезок в натуре между точками n и m составляет 0,5 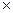35,7=17,85 м.

Приведем обратный пример: На плане масштаба 1:1000 требуется построить отрезок g h , равный в натуре 17,4 м. Согласно данному масштабу основание поперечного масштаба на местности равно двадцати метрам, интервал соответствует двум метрам, а при подъёме на одну горизонталь приращение равно двадцати сантиметрам. Раствор циркуля-измерителя при такой длине отрезка должен включать 8 интервалов и приращение при подъёме на седьмую горизонталь.

По другой методике 17,4 м в натуре соответствуют 17.4 мм. на плане, что меньше основания поперечного масштаба. Раствор циркуля-измерителя должен включать 8 интервалов и приращение 17,4 - 8 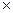2=1,4 мм. Искомый отрезок будет расположен на 1,4:0,2=7 горизонтальной линии и заключен между вертикальной линией ob и кососекущей, отсчитывающей от точки О 8 делений.

Вопросы для проверки

1. Что называют числовым масштабом?

2. Что называют линейным масштабом, его основанием? К его строят? Показать на примере.

3. Какие масштабы приняты для карт и какие для планов?

4. Что называют точностью масштаба? Практическое значение точности масштаба. Показать это на примере.

5. Для чего существует поперечный масштаб? Как его строят?

6. Привести примеры на использование поперечного масштаба.

ii. определение площадей планиметром

полярный планиметр. Планиметрами называют приборы, предназначенные для измерения площадей криволинейных фигур на плоскости. В геодезической практике повсеместно применяется полярный планиметр. В упрощенном виде этот планиметр изображен на рис. 4.

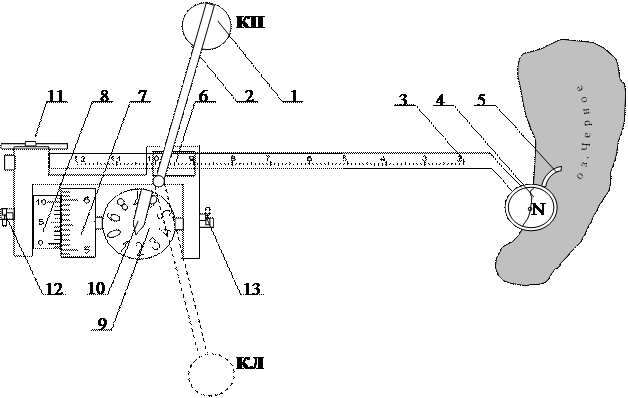
Рис.4

Его основными частями являются:

· полюс 1 в виде груза с иглой в основании;

· полюсный рычаг 2, имеющий на другом конце штифт;

· обводной рычаг 3 со шкалой, выпуклой линзой 4 и с ручкой 5;

· каретка 6 со счетным механизмом;

· счетное колесо 7 счетного механизма;

· верньер 8 счетного колеса 7;

· диск 9 с циферблатом;

· указатель отсчетов 10 на диске 9;

· опорный ролик 11.

Благодаря штифту полюсного рычага 2, обеспечивающему шарнирную связь с кареткой 6, этот рычаг может находиться под любым углом к обводному рычагу 3. Каретка 6 со счетным механизмом может перемещаться вдоль обводного рычага 3 и закрепляться на нем, позволяя тем самым устанавливать желаемую рабочую длину рычага, отсчитываемую от центра выпуклой вниз линзы 4. Рабочая длина обводного рычага 3 фиксируется взятием по нему отсчета с помощью верньера на каретке 6. Вращение счетного колеса 7 с помощью червячной передачи вызывает вращение диска 9 на 0,1 оборота. Циферблат диска 9 имеет 10 оцифрованных делений, а колесо 7 - 100 делений, оцифрованных через каждый десяток. Отсчеты по колесу 7 берутся с помощью верньера 8 с учетом порядкового номера совпадающего штриха.

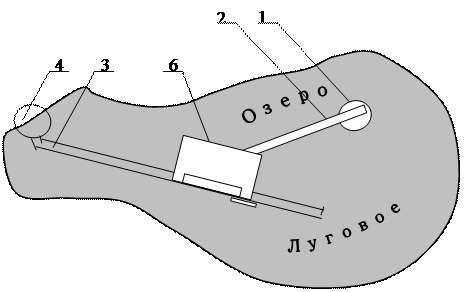Рис.5

Таким образом, отсчет на отсчетном механизме берут в виде четырехзначного числа: целые тысячи берут по диску 9, сотки и десятки – по счетному колесу 7, единицы – по порядковому номеру совпадающего штриха верньера 8. Заметим. что сотни и десятки отсчета по колесу 7 берутся по нулевому штриху верньера 8. Отсчет, который представлен на рис. 4, будет 1515. Среди прочих погрешностей, возникающих при измерении площадей, немалое значение имеет погрешность за неперпендикулярность плоскости колеса 7 и оси обводного рычага. В значительной степени эту погрешность можно устранить путем расположения полюса 1 по обе стороны от обводного рычага 3: площадь контура определяют дважды -- при одном положении полюса и при другом, принимая за результат среднее значение. На рис. 4 положение полюса 1, изображенного сплошной окружностью, называют КП: счетное колесо 7 находится правее направления полюсного рычага 2 при взгляде со стороны полюса 1. Положение же полюса, изображенного пунктирной окружностью, называют КЛ: счетное колесо 7 находится при взгляде со стороны полюса левее направления полюсного рычага.

o условия, необходимые для нормальной работы планиметра.

· План (карта) должен быть свободен от складок, для чего он натягивается с помощью кнопок на гладкую горизонтальную поверхность стола или чертежной доски.

· Счетное колесо 7 должно свободно, но без колебательных движений вращаться и передовать свое вращение диску 9 с циферблатом. Достижение такого вращения колеса 7 производится винтами 12 и 13.

· Ширина зазора между колесом 7 и его верньером 8 должна быть минимальной, не более листа тонкой бумаги. Она регулируется винтами, с помощью которых верньер 8 прикреплен к каретке 6.

· Ручку 5 при обводе контура с определяемой площадью обводным рычагом 3 нужно держать свободно, без напряжения, чтобы линза 4 с фиксированным ценром опиралась на бумагу только своим весом и частично весом обводного рычага 2.

· Счетный механизм должен быть отрегулирован так, чтобы при любом круглом отсчете по циферблату диска 9 отсчет по счетному колесу 7 был близок к нулю.

сущность работы с планиметром заключается в следующем.

Случай 1. Полюс 1 располагается вне контура с определяемой площадью. На контуре фиксируют произвольную точку N, на которую затем устанавливают фиксированный центр линзы 4 и берут отсчет по планиметру U₁. С помощью ручки 5 производят обвод по всему контуру до возврещения центра линзы 4 к точке N и снова берут отсчет U₂ по отсчетномо механизму. Искомую площадь находят по формуле:

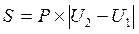
где:P – цена деления планиметра, то есть та площадь, при обводе которой отсчет по планиметру изменяется на единиу. Она может выражаться в квадратных сантиметрах плана (карты) или в гектарах на местности (в натуре);

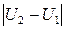– абсолютное значение разности отсчетов.

Цену деления Р определяют путем обвода контура с известной площадью S со взятием отсчетов U₁ и U₂ соответственно до обвода и после обвода, Величину Р нахсдят по формуле:

;

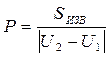Для определения Р в качестве контура с известной площадью можно взять квадрат километровой сетки карты. Кроме этого в комплекте планиметра имеются приспособления для построения контуров с известной площадью.

Случай 2. Полюс 1 планиметра располагается внутри контура с определенной площадью (рис. 5). Этот случай возникает, когда обвод контура с полюсом вне его становится невозможным из-за больших размеров контура. Здесь приведенная выше формула для получения определенной площади S не годится. В учебной литературе приводится формула:

;

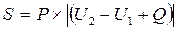где Р – цена деления планиметра;

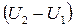-- разность между начальным отсчетом и отсчетом после обвода;

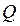– постоянное число планиметра, не имеющее размерности.

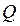определяют путем обвода одного итого же контура с известной площадью дважды – с расположением полюса 1 вне контура и в пределах контура, при этом используют формулу:

;

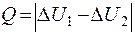где 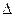U₁ – разность отсчетов после обвода и до обвода с расположением полюса 1 вне контура;

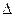U₂ –то же, но с расположением полюса 1 внутри контура.

порядок работы с планшетом.

Перед определением площади исполнитель работы должен знать цену деления планиметра, которая зависит от длины рычага 3, отсчитываемой по верньеру каретки 6, примыкающему к этому рычагу. Поэтому нужно иметь под рукой данные о том. какой длине рычага соответствует то или другое известное значение цены деления. Если таких данных нет, то приходится перед измерением определять цену деления при той длине обводного рычага 3, на которой установлена каретка 6.

Удобно в качестве фигуры с известной площадью брать квадрат километровой сетки карты. Пусть участок земной поверхности, площадь которого нужно определить, изображен на карте масштаба 1: 25000, на которой квадрат километровой сетки имеет размер 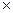: 4 см 4 см.

К выбранному квадрату пристраивают планиметр с полюсом 1 в любом положении КП или КЛ и бегло обводят выбранный квадрат, следя при этом, чтобы рычаги 2 и 3 не становились под углом более 150 или менее 30 градусов. Выбирают исходную точку обвода (какой-либо угол квадрата) и берут отсчет, который записывают в графу 3, строку 1 ведомости (табл. 1).

Ведомость определения цены деления планиметра № 12739

при длине рычага 1257

Таблица 1

№ строки	Положение полюса	Отсчеты	Разность отсчетов	Средняя разность	Неизвестная площадь	Цена деления
	КП			171,5	16 см2	0,094 см2
	КЛ

Далее производят обвод контура квадрата по всему периметру до возвращения центра линзы 4 в исходную точку и берут отсчет, записывают в графу 3, строку 3. Осторожно, сдвигая с исходной точки центр линзы 4, меняют положение полюса. Если при этом отсчет действительно не изменился, то его переписывают в строку 3, графу 3. Если отсчет был сбит, то ценр линзы снова устанавливают на исходную точку и снова берут отсчет, который записывают в строку 3, графу 3. Отсчет, взятый по окончании обвода квадрата, записывают в графу 3, строку 4. Разности между отсчетами при КП и КЛ не должны превосходить 5 единиц. При несоблюдении этой нормы оба обвода повторяют.

Значение цены деления, вычисленное по формуле:

,

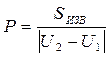записывают в графу 7 ведомости.

Процесс измерения площадей земельных участков, закрытых водоемов и других обьектов протекает точно так же, как и при определении цены деления. Записи отсчетов и результаты вычислений также ведут в специальной ведомости (табл. 2).

Ведомость измерения площади озера черного.

Планиметр № 12739 ; длина обводного рычага – 1257 ;

масштаб карты – 1: 25000 Таблица 2

Положение полюса	Отсчеты	Разность отсчетов	Средняя разность отсчетов	Цена деления (См 2)	Площадь   ( См 2)	Число гектаров в натуре в 1 кв. см на карте, ( га )	Площадь ( га)
КП				0,094	31,008	6,25	195,05
КЛ

По приведённой в графе 7 (табл.2) записи поясним как получают число гектаров в натуре в 1 см² карты. Согласно масштабу 1:25000 одному сантиметру на карте соответствует 250 м. Следовательно, площадь 1 см² на карте соответствует 250 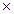250=62500м² в натуре, что означает 6,25 га.

При работе с планиметром часто возникают случаи, когда отсчёт, взятый после обвода, оказывается меньше отсчёта, взятого перед обводом контура, при обводе контура по ходу часовой стрелки. В этих случаях к отсчёту, взятому после обвода, прибавляют один оборот диска 9, то есть 10000 единиц.

При обводе контура против хода часовой стрелки отсчёт, взятый после обвода, должен быть меньше отсчёта, взятого до обвода. Если случается обратное, то к отсчёту, взятому до обвода, прибавляют 10000 единиц. Относительная погрешность измерения площадей полярным планиметром может быть достигнута 0,5%.

Вопросы для проверки

1. Для чего предназначен полярный планиметр?

2. Какая относительная погрешность измерения площади может быть достигнута планиметром?

3. Из каких основных частей состоит планиметр?

4. Что такое цена деления планиметра?

5. Как определяют цену деления планиметра и в каких единицах она выражается?

6. Как пользуются полярным планиметром при измерении площадей? Формулы?

7. Что такое постоянное число планиметра?

8. От чего в данном планиметре зависят цена деления и постоянное число?

9. Для чего измерение площадей производят при положениях полюса КП и КЛ?

iii. номенклатура листов карт и планов

ОБЩИЕ ПОЛОЖЕНИЯ. В целях наиболее эффективного использования в народном хозяйстве топографических карт и планов, насчитывающих многие миллионы экземпляров только в единичном исполнении, введена система их обозначения, которая называется номенклатурой.

Номенклатурное обозначение проставляется на самом видном месте листа карты (плана). Номенклатурное обозначение на листе называют просто – «номенклатура». Зная номенклатуру того или другого листа карты (плана) и не имея его в наличии, можно определить (для карт) и место расположения изображенного на листе района относительно начального меридиана и экватора. Чтобы решение такой задачи могло выполняться с помощью номенкпатуры за основу ее построения взят лист миллионной карты, то есть лист карты 1:1000000.

НОМЕНКЛАТУРА ЛИСТА МИЛЛИОННОЙ КАРТЫ складывается из обозначения номера колонны (на которые планета разбита меридианами через 6 градусов, начиная от меридиана с долготой 180 градусов в направлении на восток) и обозначения в виде заглавной буквы пояса (на которые разбито северное полушарие планеты параллелями, начиная от экватора в направлении на север) (рис. 6.).

Пояса и колонны, пересекаясь, образуют трапеции, каждая из которых изображается одним листом миллионной карты. Так, например, участок земной поверхности, заполняющий трапецию, с городом Москва может быть изображен на листе с номенклатурой N – 37, с городом Владивосток – L –53 и т.д.

ОБРАЗОВАНИЕ НОМЕНКЛАТУРЫ ЛИСТОВ КАРТ ДРУГИХ МАСШТАБОВ происходит следующим образом.

Следующим по масштабному ряду идет масштаб 1:500000. Номенклатура листов карты этого масштаба образуется путем деления листов карты масштаба 1:1000000 на 4 части меридианом через 3 градуса и параллелью через 2 градуса (рис.7). Каждая часть получает обозначение в виде заглавной буквы русского алфавита. Приписыванием буквенного обозначения той или иной части к номенклатуре листа миллионной карты получают номенклатуру соответствующего листа карты масштаба 1:500000. Например, лист карты этого масштаба с городом Москва имеет номенклатуру – N – 37 – B (рис.8), а последний лист трапеции N – 37 – номенклатуру N – 37 – Г. Заметим, что если внутренняя рамка листа масштаба 1:500000 – 3 градуса и 2 градуса, соответственно.

Номенклатуру листа карты масштаба 1:200000 получают делением на 36 частей листа миллионной карты (на 6 рядов по долготе через 1 градус и на 6 рядов по широте через 40 градусов). Каждая часть получает свой номер в виде римских цифр. Причем, порядок нумерации тот же, что и для буквенных обозначений. номенклатуру листов масштаба 1:200000 получают приписыванием к листу миллионной карты номера соответствующей части. Так, например, последний лист (часть) трапеции N – 37 в масштабе 1:200000 имеет номенкпатуру N – 37 – 36.

Номенклатура листов карт масштаба 1:100000 образуется от деления листа миллионной карты на 144 части (12 рядов по долготе через 6:12=30 минут меридианами и 12 рядов по широте через 4:12=20 минут параллелями). Каждой части присваивается порядковый номер из арабских цифр (рис.9). Приписывая номер части к номенклатуре листа миллионной карты, получают номенклатуру соответствующего листа карты масштаба 1:100000 (рис.10). Номенклатура последнего листа карты масштаба 1:100000, относящегося к трапеции N – 37 (то же что иноменклатура листа миллионной карты этой трапеции) будет N – 37 144. Заметим, что номенклатура последнего листа характерна тем, что она показывает на сколько частей разбивается лист карты предыдущего (более мелкого) масштаба и какое обозначение эти части получают.

Дальнейшее образование номенклатур можно выразить в табличной форме (табл.3).

Образование номенклатуры листов карт

Таблица 3

Масштаб	Номенклатура получается делением листа	Размеры рамки	Номенклатура последнего листа
Какого масштаба	На сколько частей	По долготе	По широте
1:1000000	—	—	6˚	4˚	N – 37
1;500000	1:1000000		3˚	2˚	N – 37 – Г
1:200000	1:1000000		1˚	40’	N – 37 – 36
1:100000	1:1000000		30’	20’	N – 37 – 144
1:50000	1:100000		5’	10’	N – 37 –144 – Г
1:25000	1:50000		7,5’	5’	N – 37 – 144 – Г – г
1:10000	1:25000		3,75’	2,5’	N – 37 – 144 – Г – г – 4
1:5000	1:100000		1’52,5”	1’15”	N – 37 – 144 – (256)
1:2000	1:5000		37,5”	25”	N – 37 – 144 – (256 – и)

Примечание. Таблица построена на примере трапеции N – 37 с городом Москва.

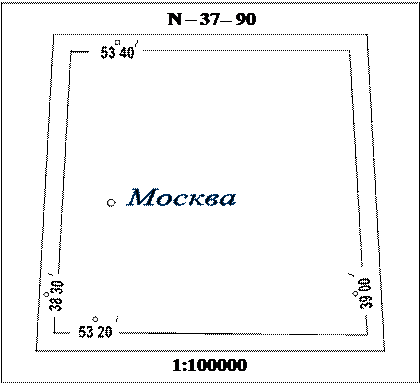Рис.10

НОМЕНКЛАТУРА ЛИСТОВ ТОПОГРАФИЧЕСКИХ ПЛАНОВ.

Если внутренние рамки топографических карт представляют собой меридианы и параллели, то по форме они являются трапециями. Топографические планы в планшетном исполнении имеют внутреннюю рамку в форме квадрата.

За основу квадратной разгравки планов и их номенклатуры принима лист (планшет) масштаба 1:5000, внутренняя рамка которого имеет размеры 40 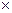40 см, что в переводе в натуру означает 2 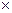2 км или 400 га. Порядок нумерации этих листов устанавливается главным архитектором города.

С перспективой развития город (район) оконтуривается. Внутриконтурное пронстранство с помощью карт масштаба 1:10000 делится на квадраты со сторонами в 2 км, площадью 400 га (рис. 11). Каждый квадрат получает свой порядковый номер из арабских цифр. Листы плана города (района) масштаба 1:5000 как раз и представляют изображения этих квадратов. Номер квадрата является номенклатурой соответствующего листа плана масштаба 1:5000 (см.рис.11).

Рис.11

Для получения номенклатуры листа плана города (района) в масштабе 1: 2000 лист масштаба 1:5000 делят на 4 равных квадрата с площадью 100 га каждый (что означает 1 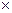1 км). Каждый квадрат изображается в масштабе 1:2000 отдельным листом (планшетом) с внутренними рамками 50 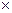50 см.

Номенклатура таких листов складывается из номенклатуры соответствующего листа масштаба 1:5000 и буквенного обозначения квадрата (рис.12).

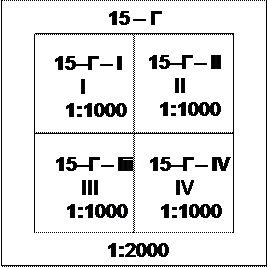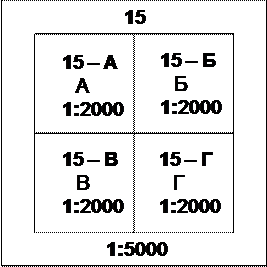Рис.12 Рис.13

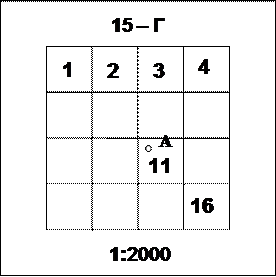
Номенклатура листов плана масштаба 1:1000 образуется по аналогичной схеме, только на 4 части делят лист масштаба 1:2000 и обозначают каждую часть своим порядковым номером в виде римских цифр (рис.13).

Рис.14 Рис.15

Так же образуется и номенклатура листов планов масштаба 1:500. При зтом делят лист масштаба 1:2000 на 16 частей, которые пронумеровывают арабскими цифрами (рис.14.15).

Образование номенклатуры листов топографических планов изображено в сжатой форме в таблице 4.

Образование номенклатуры листов топографических планов Таблица 4

Маштаб листа, номенклатура которого определяется	Номенклатура образуется делением листа	Размер рамки листа с определяемой номенклатурой, (см )	Пло щадь листа в натуре	Номенклатура последнего листа
Масштаба	На сколько частей
1:5000	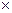—	—	40 40
1:2000	1:5000	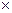	50 50		15 – Г
1:1000	1:2000	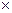	50 50		15– Г – 4
1:500	1:2000	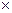	50 50	6,25	15 – Г – 16

Примечание: Последняя графа заполнена на примере заштрихованного квадрата на рис. 11. Эта графа показывает, как нужно записать искомую номенклатуру на примере последнего листа.

Упражнения

1. Определить номенклатуру листа миллионной карты с городом Новосибирск (рис.6).

2. Определить номенклатуру листа карты масштаба 1:500000 с городом Владивосток (рис.6).

3. Определить географические координаты юго-западного угла рамки листа, имеющего номенклатуру С – 5.

4. Определить географические координаты северо-восточного угла рамки листа с номенклатурой N – 37 – 12 и масштаб зтого листа.

5. Широта города 59˚ , долгота 61˚ . Определить номенклатуру листа карты масштаба 1:100000.

6. Река на территорию обозреваемого листа плана с номенклатурой 25 – В течет с севера. По листу какой номенклатуры и какого масштаба можно проследить за течением реки севернее территории обозреваемого листа карты.

7. Какой масштаб листа плана с номенклатурой 17 –Г –4 . Какая номенклатура листов этого же масштаба, изображающих соседние территории с запада, севера и востока с территорией листа названной номенклатуры.

Вопросы для проверки.

1. Что такое номенклатура?

2. В чем состоит ее польза?

3. Как получают номенклатуру листа миллионной карты и какова ее роль в получении получении других номенклатур карт?

4. Как получают номенклатуру листов планов масштаба 1:5000 и какова роль этой ноиенклатуры в образовании других номенклатур?

5. Привести примеры образсвания номенклатур карт.

6. Привести примеры образования номенклатур планов.

IV. РЕШЕНИЕ ЗАДАЧ НА ТОПОГРАФИЧЕСКОМ ПЛАНШЕТЕ

IV.1. РАЗГРАФКА РАМОК ТОПОГРАФИЧЕСКИХ КАРТ.

Лист топографической карты, как и лист плана, в стандартном исполнении называют топографическим планшетом. К разграфке планшетов топографических карт относят внутреннюю рамку, градуировку линий рамки, километровую сетку. Поскольку участок земной поверхности, изображенный на планшете карты имеет своими границами меридианы и параллели, то рамка планшета имеет трапециевидную форму.

В качестве примера разграфки планшета топографической карты на рис.16 рассмотрен планшет с номенклатурой Р – 51 – 13 . Подготовленный студент узнает в нем масштаб 1:100000. Северная и южная линии внутренней рамки этого планшета – параллели. Широта их 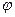₁ = 63˚20’ и 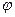₂ = 63˚40’. Западная и восточная линии рамки – меридианы с долготой 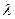₁ = 120˚00’ и 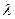₂ = 120˚30’. Указанные географические координаты линий рамки подписываются на ее углах и они строго соответствуют номенклатуре. Как видно, размеры рамки по широте составляют 20’, а по долготе – 30’. Именно на эти количества делений разбиты соответственно боковые и горизонтальные линии рамки.

Решение многих задач на планшете связано с плоской прямоугольной системой координат. Поэтому на планшете наносят так называемую километровую сетку в виде системы квадратов с общими сторонами и вершинами. Одни стороны этих квадратов параллельны проекции осевого меридиана (т.е. ,оси Х), другие – проекции на горизонтальную плоскость экватора. Свое название эта сетка получила по длинам сторон квадратов, выраженным целым числом километров.

Каждая линия километровой сетки в непосредственной близости от рамки обозначается своими координатами. Координаты У выражают расстояние линий от осевого меридиана (точнее – его проекции), а координаты Х – от экватора.

Как известно, за начало координат в каждой зоне принимается точка пересечения осевого меридиана с экватором. Для исключения знака минус координаты У для точек, находящихся в западной половине зоны, эта координата для осевого меридиана принята не за нуль, а за 500 км.

Для планшетов, относящихся к западной половине зоны, подписанные на планшетах координаты линий километровой сетки поэтому всегда будут меньше 500 км, ибо эти координаты в направлении на запад убывают. Например, если координата У линии сетки, подписанная на планшете, будет 375 км, то это значит, что расстояние данной линии до осевого меридиана составляет 125 км, и что она находится западнее осевого меридиана.

Для планшетов же, относящихся к восточной половине зоны, координаты У линий сетки будут на столько больше 500 км, сколько километров отделяют их от осевого меридиана. Перед значением координаты У левой крайней и правой крайней линий сетки приписывают номер зоны, определяемый вычитанием из номера шестиградусной колонны величины 30 (число колонн в западном полушарии). Это замечание касается всей территории России.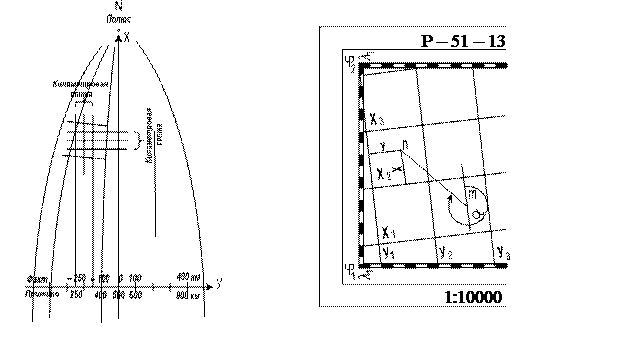

Рис.16 Рис.17

Рис. 16 демонстрирует причину перекоса линий километровой сетки относительно рамок планшета.

Значительно проще обстоит дело с разграфкой планшетов топографических планов. Их внутренняя рамка имеет форму квадратов 40 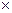40 см, или 50 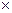50 см. На рабочей части планшета, заключенной во внутреннюю рамку, разбивается координатная сетка в виде одинаковых квадратов линиями, паралельными линиям рамки. Интервал между линиями принимают или 5 см, или 10 см. Координаты линий оцифровывают целыми сотнями или полусотнями метров.

IV.2 ОПРЕДЕЛЕНИЕ ПРЯМОУГОЛЬНЫХ КООРДИНАТ ТОЧКИ показано на рис.17. Координаты точки n могут быть записаны так:

Х_n = Х₂ + x

У_n = У₁ + у

Величины Х₂ и У₁ берут в виде готовых величин с планшета. Величины х и у измеряют с помощью поперечного масштаба.

IV.3. ОПРЕДЕЛЕНИЕ ДИРЕКЦИОННОГО УГЛА НАПРАВЛЕНИЯ С ТОЧКИ НА ТОЧКУ представлено на рис.17. Определение дирекционного угла 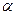_mn производят графическим способом. Для этого по только что показанному методу определяют координаты точек m и n – по формуле:

r_mn = arctg ( У_n — У_m ) ( X_n — X_m ) ;

вычисляют румб определяемого направления.

По знакам числителя и знаменателя определяют название румба.

При этом пользуются табл. 5.

Таблица 5

Знаки числителя и знаменателя	Название румба
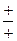	СВ
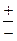	ЮВ
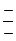	ЮЗ
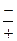	СЗ

Рис.18 Рис.20

IV.4. ОПРЕДЕЛЕНИЕ ВЫСОТНОЙ ОТМЕТКИ ТОЧКИ производят следующим образом. Через точку (на рис.18 точка С) проводят линию наиболее близкую к нормали соседних горизонталей. Измеряют отрезоки се и сf . Превышение точки c над точкой е будет:

;

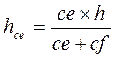а превышение точки f над точкой c будет:

.

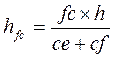В этих формулах h -- высота сечения рельефа, берется готовой с планшета, высотную отметку точки С можно определить по одному из выражений:

;

.

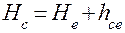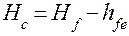IV.5. ПОСТРОЕНИЕ ПРОФИЛЯ МЕСТНОСТИ НА ЗАДАННОМ ОТРЕЗКЕ. Заданный отрезок ав (рис.18), в пределах которого требуется построить профиль, без изменения масштаба переносится вместе с точками его пересечения горизонталями на лист будущего профиля (рис.19).

Перечерченный отрезок принимают за условный горизонт, которому придают численное значение в виде круглой сотни или круглого десятка метров. Величина условного горизонта подбирается таким образом, чтобы между будущим профилем и перенесенным отрезком оставалось на чертеже пространство.

С левой стороны отрезка, начиная от него, строят шкалу высот исчисление которых ведется от условного горизонта. Построение и оцифровка шкалы высот ведется в масштабе в 10 раз более крупном, чем масштаб планшета. Из точек пересечения отрезка горизонталями восстанавливают перпендикуляры, по которым откладывают их высотные отметки в соответствии со шкалой высот. По полученным на перпендикулярах точкам строят ломанную, которая и является профилем.

IV.6. ОПРЕДЕЛЕНИЕ КРУТИЗНЫ СКАТА производится с помощью масштаба заложений, изображаемого на всех топографических планшетах (рис.20) и представляющего собой график зависимости заложений от угла наклона земной поверхности. Заложение k l (рис.18) циркулем - измерителем переносят на масштаб заложений так, как это показано на рис.20. Нижняя ножка циркуля показывает угол наклона местности. На данном примере этот угол (крутизна) равен 5˚20’.

IV.7. ТРАССИРОВАНИЕ С ЗАДАННЫМ УКЛОНОМ производится перед выносом проектного положения вытянутых объектов в натуру. Предположим, что из точки m к точке n (рис.18) требуется проложить трассу с уклоном местности не более заданного уклона 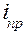. Основываясь на том, что

,

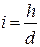где: 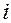– уклон выбранного направления с одной точки на другую;

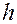– превышение одной точки над другой;

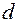– заложение;

можем записать:

.

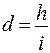Величина 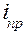задается, исходя из технических условий эксплуатации, а 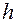принимают равным высоте сечения рельефа для данного планшета.

Вычисленное по вышеприведенной формуле значение 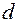набирается по линейке циркулем и из точки m на соседней горизонтали в направлении на точку n делают две засечки. Точки пересечения 1 и 1^’ соединяют прямой с точкой m. Если засечки не получаются (горизонталь отстоит достаточно далеко), то это будет означать, что трасса должна проходить от точки m до следующей горизонтали, соблюдая направление на точку n , в таком случае наклон трассы на указанном отрезке будет меньше заданного, что и требуется. Из точек 1 и 1’ на следующей горизонтали делают новые засечки, но в направлениях наиболее близких к направлению на точку n. Полученные новые точки 2 и 2’ соединяют прямыми соответственно с точками 1 и 1’ и т.д. вплоть до горизонтали точки n. От последней , полученной путем засечки, точки трасса может проходить до точки n по горизонтали. Из двух вариантов трассы выбирают наиболее подходящий с учетом таких факторов, как протяженность трассы, естественные препятствия и пр. Проложив трассу на планшете, ее затем выносят в натуру, выполняя процесс, обратный съемке.

IV.8. ПОЛУЧЕНИЕ НА ПЛАНШЕТЕ ГРАНИЦ ВОДОСБОРНОЙ ПЛОЩАДИ.

Необходимость в решении этой задачи возникает при проектировании гидротехнических сооружений (плотин, мостов, водосточных труб под полотном транспортных коммуникаций и пр.). На рис.18 изображена находящаяся в стадии проектирования автомобильная дорога, проходящая через лощину. Для определения пропускной способности трубы под дорогой необходимо определить границы водосборной площади или в некотором смысле линию водораздела. Очевидно, что границы водосборной площади, собирающей атмосферные осадки, будут проходить по самой трассе по горизонтали, от которой по обе стороны происходит понижение поверхности земли (этой горизонталью является горизонталь с отметкой 185) и по нормалям горизонталей, проходящих через точки их максимальной кривизны. На рис.18 граница водосборной площади обозначена точечным пунктиром.

Вопросы для проверки

1. Что такое топографический планшет?

2. Что такое километровая сетка?

3. Чем объясняется перекос километровой сетки относительно рамок планшета топографической карты?

4. Как узнают к какой половине зоны относится планшет?

5. Как разградуирована рамка планшета?

6. Как определяют номер зоны по номенклатуре планшета?

7. Как исключают знак минус координаты У при работе с планшетом?

8. Что такое масштаб заложений и как им пользуются?

9. Чем отличается разграфка планшетов карт от разграфки планщетов планов?

10. Отличие километровой сетки на картах от координатной сетки на планах?

11. Как находят прямоугольные координаты точки?

12. Как находят дирекционный угол направления?

13. Как находят крутизну ската?

14. Как находят высотную отметку точки?

15. Как построить профиль местности в пределах заданного отрезка?

16. Как можно на планшете протрассировать транспортную или иную магистраль с уклоном не более заданного?

17. Как определяют границы водосборной площади?Привести пример.

Литература

1. Шилов П. И. Геодезия. – М. : Недра, 1963.

2. Инженерная геодезия. Под ред. П. С. Закатова.—М.: Недра, 1976.

3. Хейфец Б. С., Данилевич Б. Б. Практикум по инженерной

геодезии. – М.: Недра, 1973.

4. Курс инженерной геодезии. Под ред. В. Е. Новака. – М.:

Недра, 1989.