Цель работы: 1)определение индуктивности катушки без сердечника и с сердечником; 2)определение емкости конденсатора;3)наблюдение явления резонанса

Приборы и принадлежности: исследуемая катушка с сердечником, воль­тметр, амперметр, реостат, источник переменного тока.

Теоретическое введение

Если в проводнике изменяется сила тока, то в нем возникает ЭДС самоиндукции, препятствующая этому изменению. ЭДС самоиндукции пропор­циональна изменению силы тока в единицу времени:

e = -L 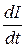(1)

Коэффициент пропорциональности L называется коэффициентом самоин­дукции и зависит от формы и размеров проводника и от магнитной прони­цаемости окружающей среды. Если предположить e = 1 В, dI/dt =1 А/с, то L = 1 Гн (Генри). Таким образом, самоиндукцией в 1 Гн обладает такой проводник, в котором изменение силы тока со скоростью 1 А в 1 сек вы­зывает ЭДС самоиндукции в 1 В. У линейных проводников коэффициент са­моиндукции мал. Большими коэффициентами самоиндукции обладают, так на­зываемые, катушки индуктивности, состоящие из большого числа витков. Пусть сопротивление постоянному току проволоки, из которой намотана катушка, равно R. Это сопротивление часто называют активным. Если включить такую катушку в цепь переменного тока, то в следствии периоди­ческого изменения силы тока возникает ЭДС индукции, препятствующая приложенному напряжению. Это приводит к тому, что сопротивление катуш­ки становится больше, чем активное. Иначе говоря, катушка индуктивнос­ти будет обладать не только активным, но и индуктивным (реактивным) сопротивлением X_L.

Если в цепь переменного тока включен конденсатор С , то вследствие периодического изменения направления тока происходит его перезарядка, что приводит к появлению емкостного сопротивления X_C.

Рассмотрим цепь, состоящую из последовательно соединенных

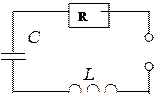сопротивления R, индуктивности L,

и конденсатора С (рис. 1)

По второму закону Кирхгофа для

замкнутого контура сумма падений

напряжений равна сумме электро-

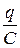движущих сил

I R + = e_оsinwt - L 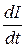(2)

Для установившегося режима колебаний решение этого уравнения име­ет вид:

I =I_o sin (wt - j) (3)

где j - разность фаз между приложенной ЭДС и силой тока.

Расчет приводит к следующим значениям амплитуды тока

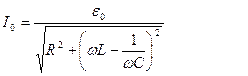(4)

разности фаз между током и внешней ЭДС

tgj =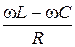

где 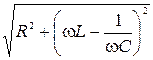= Z - полное сопротивление цепи переменного то­ка,

X_L = wL - индуктивное сопротивление; X_C = 1/wC - емкостное сопро­тивление.

В выражении (4) фигурируют амплитудные (максимальные) значения тока - I_o и ЭДС -e₀. На практике обычные вольтметры и амперметры по­казывают не максимальные, а так называемые эффективные (или действую­щие) значения I_эфф, U_эфф и e_эфф, следовательно

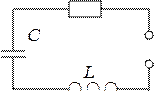
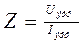(5)

_{где Iэфф = 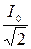; Uэфф = 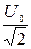; тогда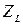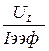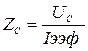} = . (5 а,б)

Если цепь состоит из источника ЭДС и емкости т.е. (R=0, L=0), то

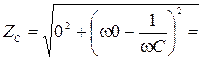
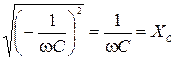откуда

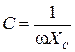(6)

Таким образом, электрическая емкость C обратно пропорциональна круговой частоте переменного электрического тока

w = 2 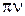(7)

где n = 50 Гц, и емкостному сопротивлению Х_с.

Если емкостное сопротивление равно нулю (Х_с = 0),то

,

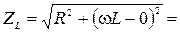
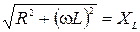откуда 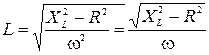(8)

Таким образом, для определения коэффициента самоиндукции катушки необходимо знать ее сопротивление Х_L, омическое сопротивление R и кру­говую частоту переменного тока w. R = 16 Ом.